- Главная
- Математика
- Презентация на тему Арифметическая прогрессия в древности

Содержание
- 2. Египетские папирусы и вавилонские клинописные таблички, относящие ко II тыс. до н.э., содержат примеры задач на
- 3. (Начало нашей эры ) Индийский царь Шерам позвал к себе изобретателя шахматной игры , своего подданного
- 4. АРХИМЕД В трудах древнегреческих математиков Евклида и Архимеда приведены правила , которые можно рассматривать как формулы
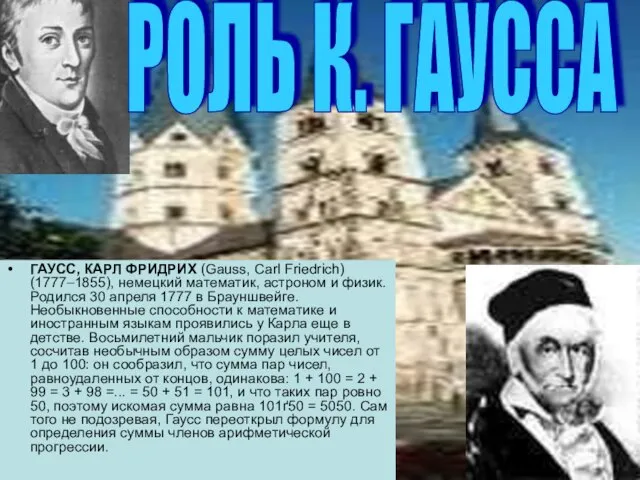
- 5. ГАУСС, КАРЛ ФРИДРИХ (Gauss, Carl Friedrich) (1777–1855), немецкий математик, астроном и физик. Родился 30 апреля 1777
- 6. Вы , наверное , заметили , что в рассмотренных примерах применялись две различные Схемы начисления процентов
- 8. Скачать презентацию
Слайд 2Египетские папирусы и вавилонские клинописные таблички, относящие ко II тыс. до н.э.,
Египетские папирусы и вавилонские клинописные таблички, относящие ко II тыс. до н.э.,

Слайд 3(Начало нашей эры )
Индийский царь Шерам позвал к себе изобретателя шахматной игры
(Начало нашей эры )
Индийский царь Шерам позвал к себе изобретателя шахматной игры

1,2,
ЕЕ сумма равна
Такое количество зерен пшеницы можно собрать лишь с площади в 2000 раз большей поверхности ЗЕМЛИ.
Геометрическая прогрессия в древности. ЗАДАЧА-ЛЕГЕНДА
Слайд 4АРХИМЕД
В трудах древнегреческих математиков Евклида и Архимеда приведены правила , которые можно
АРХИМЕД
В трудах древнегреческих математиков Евклида и Архимеда приведены правила , которые можно

Для решения задач геометрии и механики Архимед вывел формулу суммы квадратов первых n натуральных чисел:
Прогрессии древней Греции
АРХИМЕД
ЕВКЛИД
Слайд 5ГАУСС, КАРЛ ФРИДРИХ (Gauss, Carl Friedrich) (1777–1855), немецкий математик, астроном и физик.
ГАУСС, КАРЛ ФРИДРИХ (Gauss, Carl Friedrich) (1777–1855), немецкий математик, астроном и физик.
РОЛЬ К. ГАУССА
Слайд 6Вы , наверное , заметили , что в рассмотренных примерах применялись две
Вы , наверное , заметили , что в рассмотренных примерах применялись две

Схемы начисления процентов : в 1 задаче речь идет о простых процентах , в 2 задаче
Речь идет о сложных процентах.
В самых различных жизненных ситуациях очень часто приходится выполнять денежные расчеты. Рассмотрим два примера .ЗАДАЧА 1.
Ежемесячно каждая семья платит за электроэнергию в среднем 2000 сум. За каждый просроченный день взимается пеня в размере 0,5% с оплачиваемой суммы.
Сколько заплатит семья за электроэнергию, если они просрочат оплату на 1день; на n-дней?
Решение: так как 0,5% от 2000сум составляют 10 сум., то за каждый просроченный день сумма штрафа будет увеличиваться на 10 сум, и придется заплатить 2000+10=2010 сум.
ЗАДАЧА 2.
Вы , вероятно , знаете , что за хранение денег в банке вкладчику начисляют проценты. Пусть на счет в банке , который выплачивает 20% годовых , положили 1000$ и оставили эти деньги на счете на год.
Какой будет новая сумма вклада через год , через n лет?
РЕШЕНИЕ: Через год начальная сумма вклада увеличится на 20% , значит новая сумма составит от первоначальной 120%.Таким образом , через год вклад увеличится в 120/100=1,2 раза и составит 1000*1,2=1200$. Еще через год снова увеличится в 1,2 раза. Следовательно ,через 2 года на счете будет
1200*1,2=1440$
Прогрессии в жизни и быту
Вы , наверное , заметили , что в рассмотренных примерах применялись две различные
Схемы начисления процентов : в 1 задаче речь идет о простых процентах , в 2 задаче
Речь идет о сложных процентах.
 Метод Гаусса
Метод Гаусса Тренажер по логарифмам
Тренажер по логарифмам Пирамида – это многогранник, составленный из n-угольника
Пирамида – это многогранник, составленный из n-угольника Правильные многогранники
Правильные многогранники Презентация на тему Методы решения квадратных уравнений
Презентация на тему Методы решения квадратных уравнений  Задача по математике (1 класс)
Задача по математике (1 класс) Основы эконометрического моделирования
Основы эконометрического моделирования Физическое и математическое моделирование
Физическое и математическое моделирование Вычитание натуральных чисел
Вычитание натуральных чисел Новогодняя сказка в Стране математики. Для детей 5-ти лет
Новогодняя сказка в Стране математики. Для детей 5-ти лет Приём вычитания вида 15 -
Приём вычитания вида 15 - 1ce713f2e27cb837f4d7376560237c07
1ce713f2e27cb837f4d7376560237c07 Второй и третий признаки подобия треугольников
Второй и третий признаки подобия треугольников Разложение вектора по базису
Разложение вектора по базису Задачи с параметрами.Расположение корней квадратного трёхчлена
Задачи с параметрами.Расположение корней квадратного трёхчлена Краткая история появления и развития пределов
Краткая история появления и развития пределов Центральная и осевая симметрия
Центральная и осевая симметрия Презентация на тему Формулы суммы и разности синуса и косинуса
Презентация на тему Формулы суммы и разности синуса и косинуса  Части множества
Части множества Угол между прямыми в пространстве
Угол между прямыми в пространстве Стандартизированные коэффициенты регрессии
Стандартизированные коэффициенты регрессии Роль и место математики в современном мире. Пределы. Свойства пределов. Тема 1.1
Роль и место математики в современном мире. Пределы. Свойства пределов. Тема 1.1 Булева алгебра
Булева алгебра Тайна табурета деда. Исследовательская работа студентов
Тайна табурета деда. Исследовательская работа студентов Готовимся к ЕГЭ-2015 по математике. Решение 1 части реального теста ЕГЭ-2014
Готовимся к ЕГЭ-2015 по математике. Решение 1 части реального теста ЕГЭ-2014 Производная степенной функции с действительным показателем
Производная степенной функции с действительным показателем Дюжина задач на параметры
Дюжина задач на параметры Ответы к тестам для подготовки к ЕГЭ по математике
Ответы к тестам для подготовки к ЕГЭ по математике