Слайд 3Физический смысл производной
Если материальная точка движется по закону S (t), то скорость

её движения V (t) в момент времени t равна производной S‘ (t), то есть V (t) = S‘ (t).
Производная от скорости – ускорение a (t) = V‘ (t), то есть ускорение равно второй производной от функции a (t) = V‘ (t) = S“ (t).
Слайд 4Задачи на физический смысл производной
№1 Тело движется по прямой так, что расстояние

от начальной точки изменяется по закону S = 5t +0,2t² -6 (м), где t – время движения в секундах. Найдите скорость тела через 5 секунд после начала движения.
Слайд 5№2 Тело движется по прямой так, что расстояние от начальной точки изменяется

по закону S = 2t³ - 12t² + 7 (м), где t – время движения в секундах. Через сколько секунд после начала движения ускорение тела будет равно 36 м/с²?
№3 Две материальные точки движутся по законам S1 = 2,5t² -6t + 1; S2 =0,5t² +2t -3. В какой момент времени их скорости будут равны?
Слайд 6Решение задач
№1 V(t) = S‘(t) = 5+0,6t²; V(5) = 5+0,6*5² = 20

(м/с)
№2 V(t) = S‘(t) = 6t² -24t; a(t) = V‘(t) = S“(t) = 12t – 24; По условию a(t) = 36; то есть 12t – 24 = 36; t = 5 (c)
№3 V1(t) = S‘1(t) = 5t - 6; V2(t) = S‘2(t) = t+ 2; По условию V1(t) =V2(t); то есть 5t – 6 = t +2; t = 2 (c)
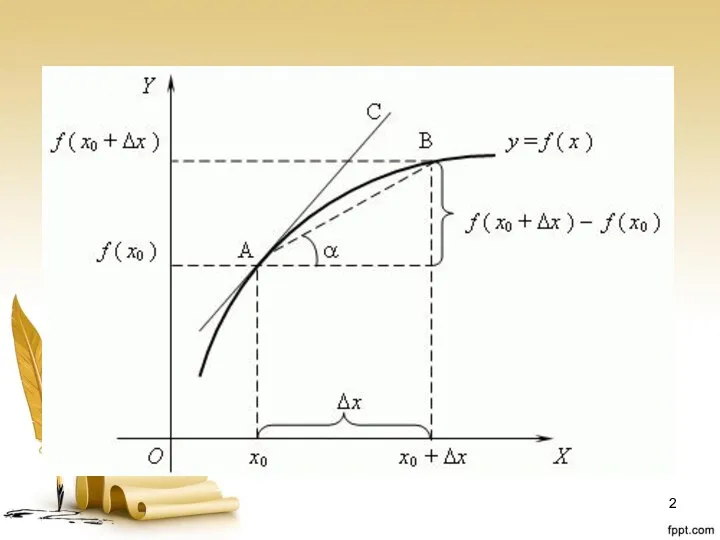
Слайд 7Геометрический смысл производной
Геометрический смысл производной состоит в том, что значение производной

функции y = f (x) в точке x равно угловому коэффициенту касательной к графику функции в точке с абсциссой x.
Слайд 8Задачи на угловой коэффициент касательной
№1 Дана функция f (x) =3x²+5x-6. Найдите

координаты точки её графика, в которой угловой коэффициент касательной к нему равен «-7».
№2 Найдите угловой коэффициент касательной, проведённой к графику функции f (x) = 4Cos x+3 в точке с абсциссой x = -/3.
Слайд 9Решение задач
№1 Ккас = f ‘(x) = 6x + 5; По условию

Ккас = -7, то есть 6х + 5 = -7; х = -2; у = f ‘(-2) = 3*(-2)² + 5*(-2) – 6 = -4; (-2; -4) – точка касания
№2 Ккас = f ‘(x) = 6*Cosx + Sinx; f ‘(/3) = 6 *Cos(/3) + Sin(/3) = 6*1/2 + √3/2 = (6 + √3)/2 ; Ккас = (6 + √3)/2 ;
Слайд 10Зависимость знаков производной от угла наклона касательной
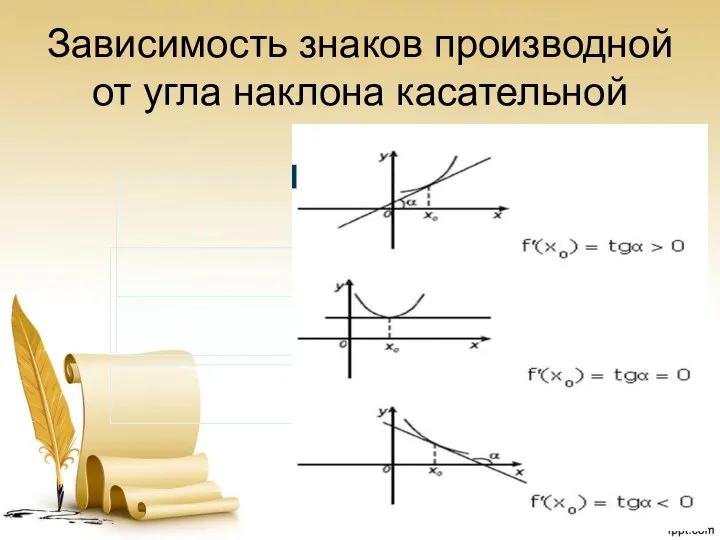









 Человек трудолюбивый – самый счастливый– самый
Человек трудолюбивый – самый счастливый– самый Распознавание графиков функций
Распознавание графиков функций Практикум по решению комбинированных уравнений
Практикум по решению комбинированных уравнений Комбинаторика
Комбинаторика Задание 2 по математике
Задание 2 по математике Сумма углов в треугольнике
Сумма углов в треугольнике Презентация на тему Группировка слагаемых. Скобки (1 класс)
Презентация на тему Группировка слагаемых. Скобки (1 класс)  Определение производной. Физический смысл производной. Приращение аргумента и приращение функции. Производная степенной функции
Определение производной. Физический смысл производной. Приращение аргумента и приращение функции. Производная степенной функции Презентация на тему Таблицы истинности
Презентация на тему Таблицы истинности  Теоремы Пифагора
Теоремы Пифагора Понятие определенного интеграла и его свойства. Формула Ньютона-Лейбница
Понятие определенного интеграла и его свойства. Формула Ньютона-Лейбница Прямоугольная система координат. Рене Декарт
Прямоугольная система координат. Рене Декарт Презентация на тему ГРАФИК ДВИЖЕНИЯ
Презентация на тему ГРАФИК ДВИЖЕНИЯ  Логические функции
Логические функции Презентация на тему Наибольшее и наименьшее значения функции
Презентация на тему Наибольшее и наименьшее значения функции  Определение арктангенса и арккотангенса числа а
Определение арктангенса и арккотангенса числа а Геометрические тела. Обьём прямоугольного параллелепипеда. 5 класс
Геометрические тела. Обьём прямоугольного параллелепипеда. 5 класс Ділення. Карточки Домана
Ділення. Карточки Домана Производная функции. Часть 1
Производная функции. Часть 1 Цифровой образовательный ресурс по алгебре. 8 класс
Цифровой образовательный ресурс по алгебре. 8 класс Применение параллелограмма
Применение параллелограмма Матрицы. Прямоугольная таблица
Матрицы. Прямоугольная таблица Декартовая система координат
Декартовая система координат Координатная плоскость
Координатная плоскость КВН Знакомьтесь: геометрия
КВН Знакомьтесь: геометрия Презентация по математике "Кафе «Математики»" -
Презентация по математике "Кафе «Математики»" -  Storymaze. Побег
Storymaze. Побег Ломаные на узорах
Ломаные на узорах