Содержание
- 2. ЦЕЛЬ: ИЗУЧИТЬ НЕКОТОРЫЕ ПРИЁМЫ ОРГАНИЗАЦИИ УСТНОГО СЧЁТА, ПОЗВОЛЯЮЩИЕ УСКОРИТЬ И РАЦИОНАЛИЗИРОВАТЬ ВЫЧИСЛЕНИЯ
- 3. Задачи: СОСТАВИТЬ АЛГОРИТМЫ ДЛЯ БЫСТРОГО ВЫЧИСЛЕНИЯ АРИФМЕТИЧЕСКИХ ДЕЙСТВИЙ- НАПРИМЕР, ДЛЯ БЫСТРОГО УМНОЖЕНИЯ ДВУЗНАЧНЫХ ЧИСЕЛ НА ДРУГИЕ
- 4. Умножение на 5, 50 1) Чтобы умножить число на 5, можно его разделить пополам, потом умножить
- 5. Умножение на 25, 250 Чтобы устно умножить число на 25 или 250, надо его разделить на
- 6. Умножение на 125 Чтобы умножить число на 125, надо его разделить на 8, а затем умножить
- 7. Умножение на 15 При умножении на 15 надо число умножить на 10 и к произведению прибавить
- 8. Умножение на 9 или 99 При умножении на 9 или 99 надо число умножить на 10
- 9. Умножение на 11 и на 101 Приемы умножения При умножении двузначного числа на 11 можно раздвинуть
- 10. Умножение на 22, 33, .... 99 Чтобы двузначное число умножить на 22, 33, ..., 99, надо
- 11. «Умножение крестиком» Пример: 53 ∙ 37 = 1961 Подпишем числа одно под другим 3 1) 5
- 12. Возведение в квадрат а² = а² - в² + в² = (а + в)(а - в)
- 13. Возведение в квадрат двузначных чисел, оканчивающихся на 5 Чтобы возвести в квадрат двузначное число, последняя цифра
- 15. Скачать презентацию












 Преобразование графиков. 8 класс
Преобразование графиков. 8 класс Презентация на тему Решение задач по теме "Пирамида" 10 класс
Презентация на тему Решение задач по теме "Пирамида" 10 класс  Десяткові і дроби
Десяткові і дроби Виды треугольников
Виды треугольников Исследование функций с помощью производных. Правила Лопиталя
Исследование функций с помощью производных. Правила Лопиталя Килограмм. Литр. Сантиметр. Дециметр
Килограмм. Литр. Сантиметр. Дециметр Презентация на тему Геометрические построения в школьном курсе математики
Презентация на тему Геометрические построения в школьном курсе математики  Обработка экспериментальных данных. Лекция 6: Регрессионный и корреляционный анализ. Нелинейная зависимость
Обработка экспериментальных данных. Лекция 6: Регрессионный и корреляционный анализ. Нелинейная зависимость Основы теории MOM метода. Настройка параметров EM симулятора на основе метода MOM
Основы теории MOM метода. Настройка параметров EM симулятора на основе метода MOM объём DVD диска
объём DVD диска Мощность множества
Мощность множества Решение треугольников
Решение треугольников Производная и исследование функции
Производная и исследование функции История аксиомы
История аксиомы Квадратные уравнения. Решение уравнений, приводимых к квадратным
Квадратные уравнения. Решение уравнений, приводимых к квадратным Создание макетов машин из геометрических фигур и тел
Создание макетов машин из геометрических фигур и тел Сравнение обыкновенных дробей
Сравнение обыкновенных дробей Числовые промежутки. Пересечение и объединение промежутков
Числовые промежутки. Пересечение и объединение промежутков Геометрическая прогрессия
Геометрическая прогрессия Решение задач по теме: Терема Пифагора
Решение задач по теме: Терема Пифагора Свойства умножения. 5 класс
Свойства умножения. 5 класс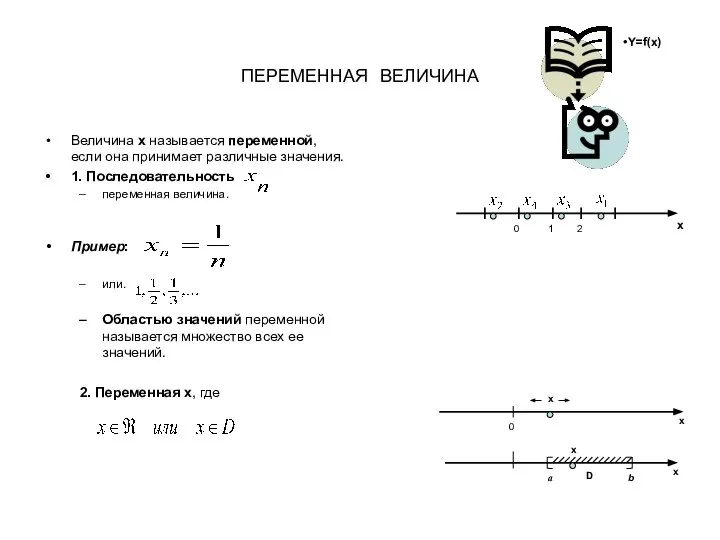 Понятие функции, предел
Понятие функции, предел Математическая психология
Математическая психология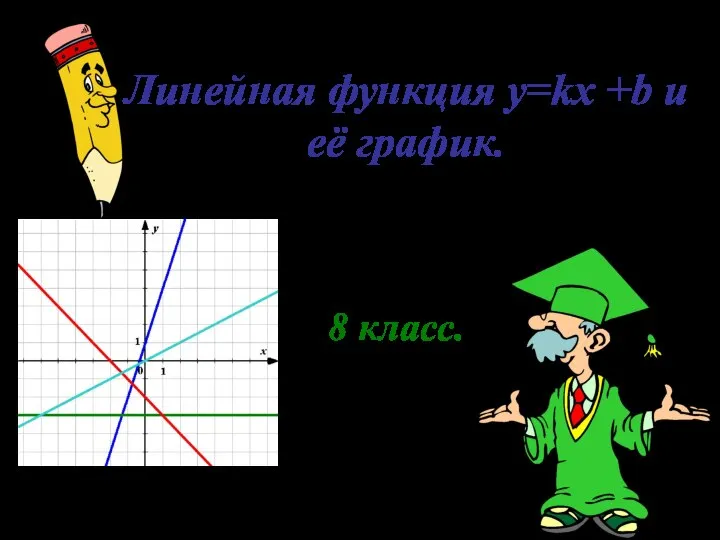 Линейная функция y=kx +b и её график. 8 класс
Линейная функция y=kx +b и её график. 8 класс Дифференциальные уравнения и их применение в медицинской практике. Тема 2.3
Дифференциальные уравнения и их применение в медицинской практике. Тема 2.3 Спин и расширенное супервремя. Суперсимметрия и суперпространство
Спин и расширенное супервремя. Суперсимметрия и суперпространство Прямоугольные треугольники
Прямоугольные треугольники Учебно – методическое обеспечение образовательного процесса по учебному предмету Математика в 2017/2018 учебном году
Учебно – методическое обеспечение образовательного процесса по учебному предмету Математика в 2017/2018 учебном году