Содержание
- 2. 4 Дифференциальные уравнения 4.1 Основные понятия Всякое уравнение, содержащее, по крайней мере, одну производную неизвестной функции,
- 3. Функция y=φ(x) называется решением дифференциального уравнения, если последнее обращается в тождество после подстановки y=φ(x). Обычно дифференциальное
- 4. Дифференциальное уравнение первого порядка имеет общий вид Дифференциальное уравнение первого порядка, разрешённое относительно , имеет вид
- 5. Условие y(x0)=y0 называется начальным условием. Общим решением дифференциального уравнения первого порядка называется функция y=φ(x,C), содержащая одну
- 6. Уравнение вида называется дифференциальным уравнением с разделёнными переменными. Алгоритм решения 1. Перенесём Q(y)dy в правую часть
- 7. 4.2.1 Дифференциальные уравнения с разделяющимися переменными Пример 1 Найти общее решение дифференциального уравнения . Решение. Заменим
- 8. Более общий случай описывают дифференциальные уравнения с разделяющимися переменными, которые имеют вид . Алгоритм решения 1.
- 9. 4.2.1 Дифференциальные уравнения с разделяющимися переменными Пример 2 Найти общее решение дифференциального уравнения Решение. Интеграл в
- 10. Таким образом, уравнение примет вид: Заменим получим Таким образом, общее решение исходного дифференциального уравнения имеет вид
- 11. Также уравнение с разделяющимися переменными может иметь вид . Алгоритм решения 1. Заменим , получим уравнение
- 12. 4.2.1 Дифференциальные уравнения с разделяющимися переменными Пример 3 Найти общее решение дифференциального уравнения Решение.
- 13. Замечание: в случае, когда в левой и правой частях дифференциального уравнения интегралы обращаются в логарифмические функции,
- 14. Дифференциальное уравнение первого порядка Pdx+Qdy=0 называется линейным, если отношение содержит лишь в первой степени (линейно). Линейное
- 15. 3. Обнуляем скобку, получая при этом новое дифференциальное уравнение с разделяющимися переменными вида , из которого
- 16. 5. Общее решение линейного дифференциального уравнения первого порядка находится путём подстановки в y=UV значения переменных U
- 17. Пример 4 Найти решение задачи Коши y(0)=2. Решение. 4.2.2 Линейные дифференциальные уравнения первого порядка Общее решение
- 18. Линейное дифференциальное уравнение первого порядка также может иметь вид . Решение аналогично, только подстановка в этом
- 19. 4.2.2 Линейные дифференциальные уравнения первого порядка Пример 5 Найти решение задачи Коши Решение.
- 20. 4.2.2 Линейные дифференциальные уравнения первого порядка Общее решение найдём из замены x=UV: Частное решение найдём, используя
- 21. 4.2.3 Дифференциальные уравнения Бернулли Дифференциальное уравнение вида (или ), где n≠0, n≠1 называется уравнением Бернулли. Схема
- 22. 4.2.3 Дифференциальные уравнения Бернулли Пример 6 Найти решение задачи Коши Решение.
- 23. 4.2.3 Дифференциальные уравнения Бернулли Общее решение найдём из замены y=UV: Частное решение найдём, используя условие Подставим
- 25. Скачать презентацию






















 Решение тригонометрических уравнений. 10 класс
Решение тригонометрических уравнений. 10 класс Величины. Длина
Величины. Длина Случайные величины 14 сен
Случайные величины 14 сен Возникновение первых математических понятий
Возникновение первых математических понятий Задачи на умножение и деление и опорные схемы к ним. Опорные схемы задач 3 класс
Задачи на умножение и деление и опорные схемы к ним. Опорные схемы задач 3 класс Умножение на 1 и 0
Умножение на 1 и 0 Диктант по геометрии
Диктант по геометрии Выбор схемы измерения переменных
Выбор схемы измерения переменных Умножение на 10,100,1000, 0,1, 0,01, 0,001
Умножение на 10,100,1000, 0,1, 0,01, 0,001 Подготовка к блиц-турниру
Подготовка к блиц-турниру Скалярное прозведение векторов
Скалярное прозведение векторов Шифр Цезаря
Шифр Цезаря Сфера и шар
Сфера и шар Многогранники. Призма
Многогранники. Призма Пропорции и проценты
Пропорции и проценты Координаты суммы, разности и произведения вектора на число
Координаты суммы, разности и произведения вектора на число Графический диктант
Графический диктант Презентация на тему Расположение точек относительно осей координат
Презентация на тему Расположение точек относительно осей координат  Найдите высоту и медиану треугольника
Найдите высоту и медиану треугольника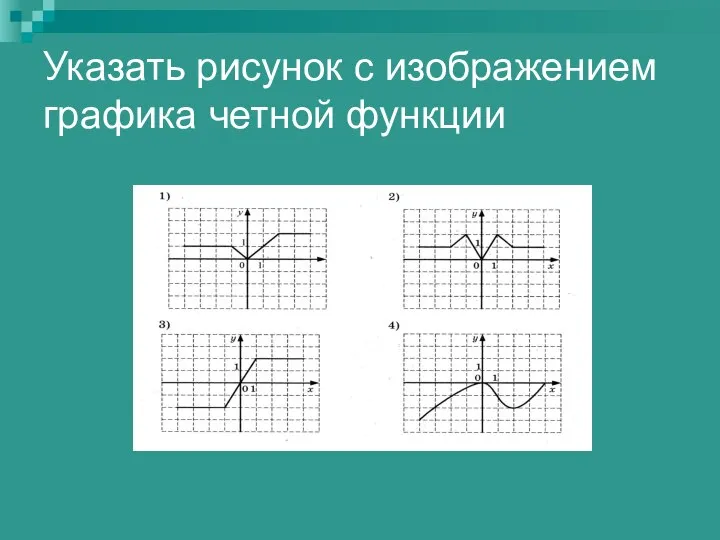 Указать рисунок с изображением графика четной функции
Указать рисунок с изображением графика четной функции Параллелепипед
Параллелепипед Выражение отношения в процентах
Выражение отношения в процентах Задачи на проценты. Схемы
Задачи на проценты. Схемы Решение нелинейных уравнений
Решение нелинейных уравнений Сложение с переходом через десяток. Тренажёр
Сложение с переходом через десяток. Тренажёр Прямоугольный параллелепипед в задачах В8 ЕГЭ. Геометрия 11 класс
Прямоугольный параллелепипед в задачах В8 ЕГЭ. Геометрия 11 класс Систематизация учебного материала по алгебре и началам анализа в 11 классе для организации повторения
Систематизация учебного материала по алгебре и началам анализа в 11 классе для организации повторения Теория вероятностей и математическая статистика
Теория вероятностей и математическая статистика