Содержание
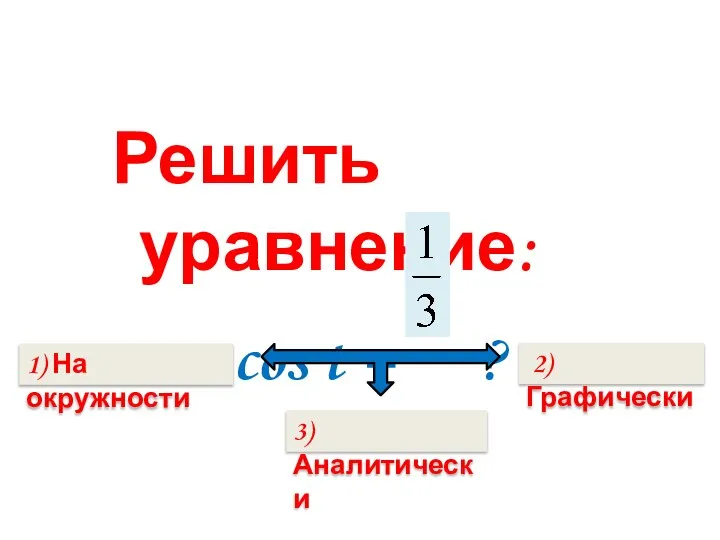
- 2. Решить уравнение: cos t = ? 1) На окружности 2) Графически 3) Аналитически
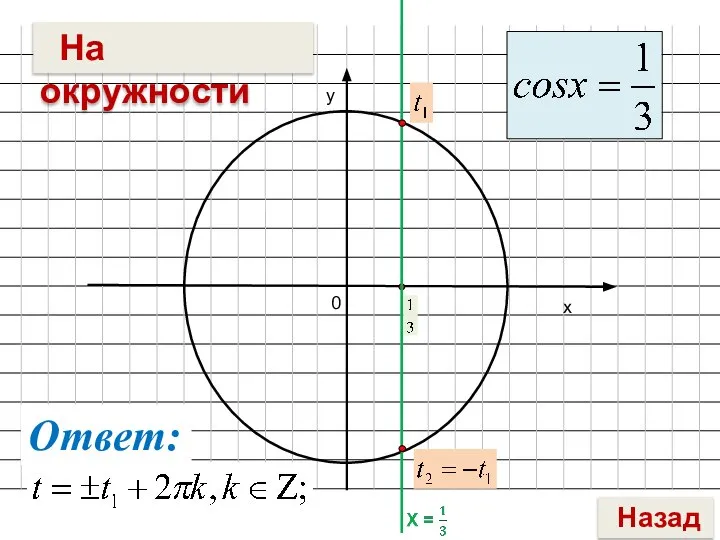
- 3. х у 0 Ответ: На окружности Назад
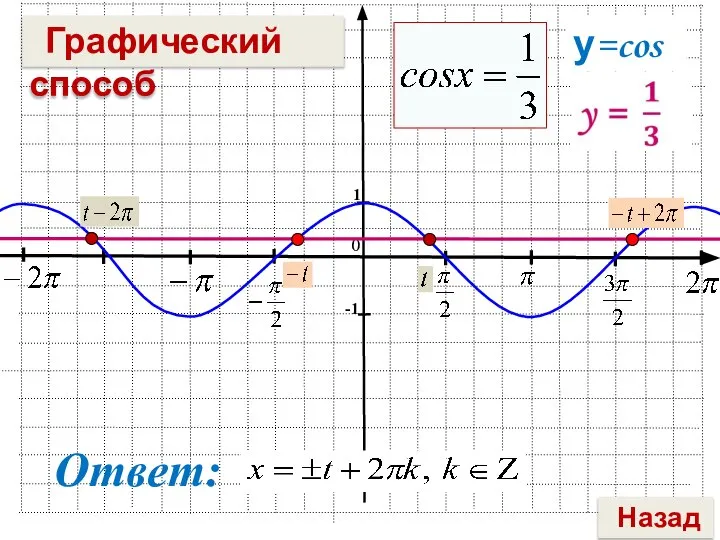
- 4. 0 Ответ: Графический способ у=cosх Назад
- 5. Аналитический способ Определить число t Примеры Составить формулы для решения уравнения Определить свойства числа t Примеры
- 6. Определение. Если -1 ≤ a ≤ 1, то arccos a = t
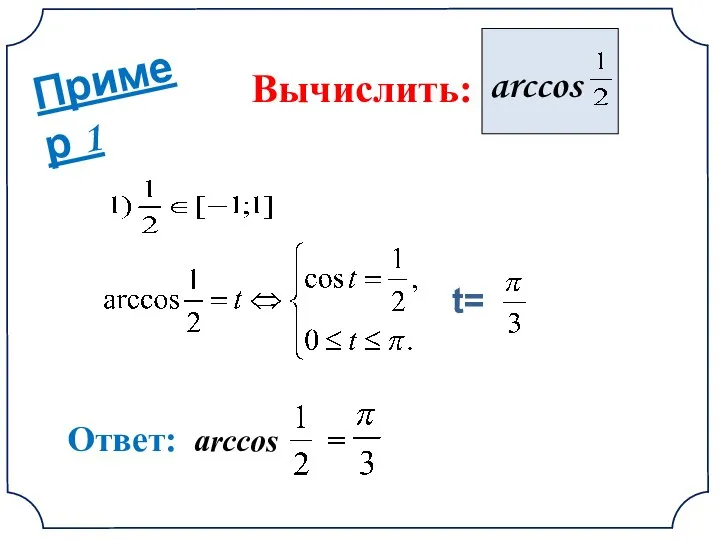
- 7. Пример 1 arccos Вычислить: Ответ: arccos = t=
- 8. Свойства арккосинуса: cos(аrccosа) = а аrccos(cost) = t аrccos(-а) = π - аrccosа -1 ≤ а
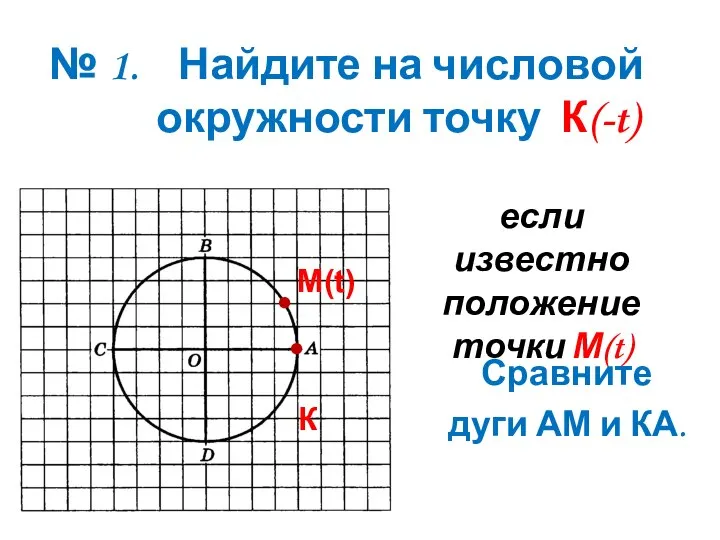
- 9. № 1. Найдите на числовой окружности точку К(-t) если известно положение точки М(t) М(t) • К
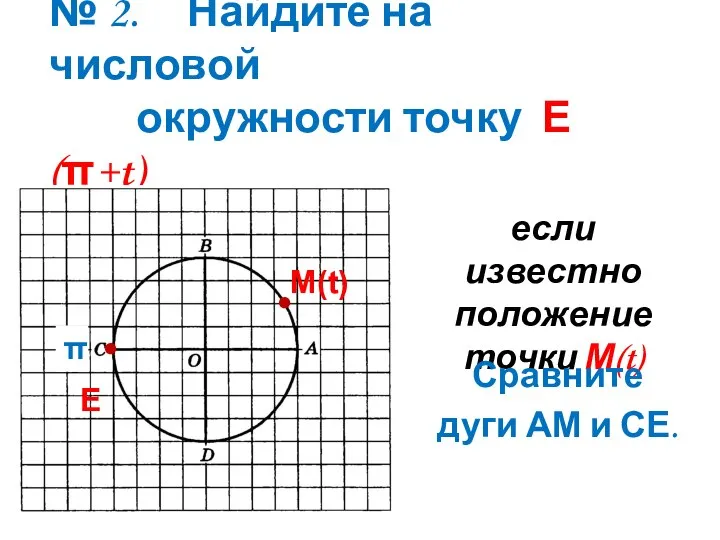
- 10. № 2. Найдите на числовой окружности точку Е(π+t) М(t) • • Е если известно положение точки
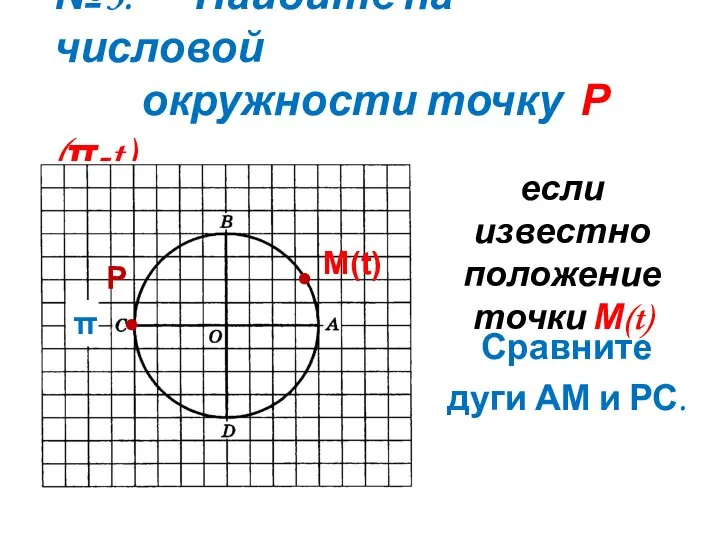
- 11. №3. Найдите на числовой окружности точку Р(π-t) Сравните дуги АМ и РС. М(t) • • Р
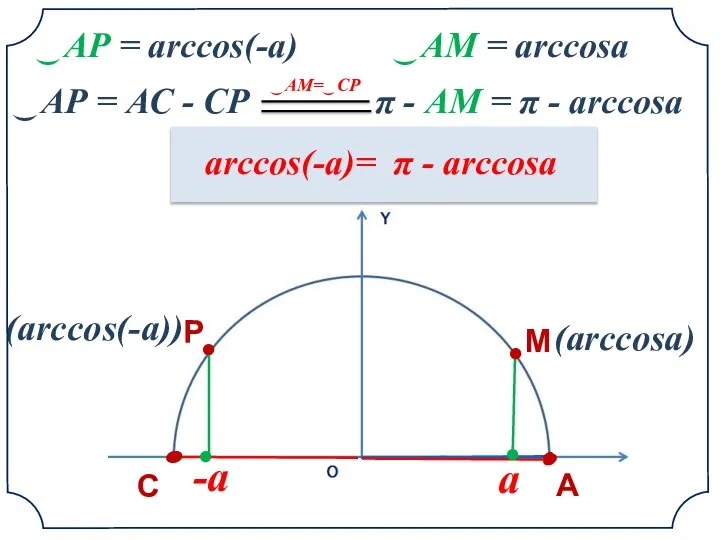
- 12. a • • -a М Р (arccosа) (arccos(-а)) ͜ АР = arccos(-а) ͜ АР = АС
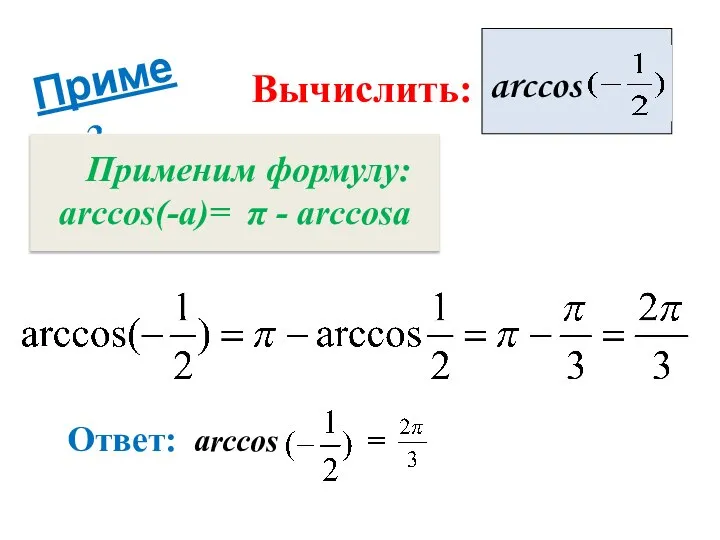
- 13. Пример 2 arccos Вычислить: Ответ: arccos = Применим формулу: аrccos(-а)= π - аrccosа
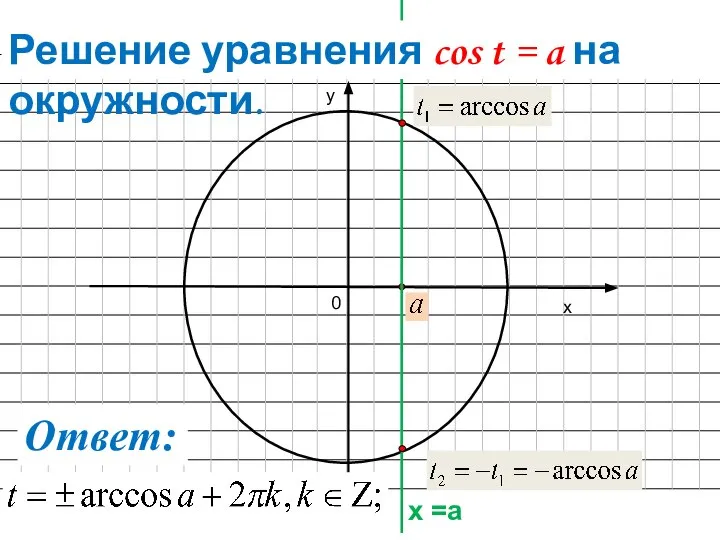
- 14. х у х =а 0 Ответ: Решение уравнения cos t = a на окружности.
- 15. МНОГО МЕСТА? ТРУДОЁМКО?
- 16. Решение уравнения cos t = a по формулам: уравнение имеет решения: Если -1 ≤ a ≤
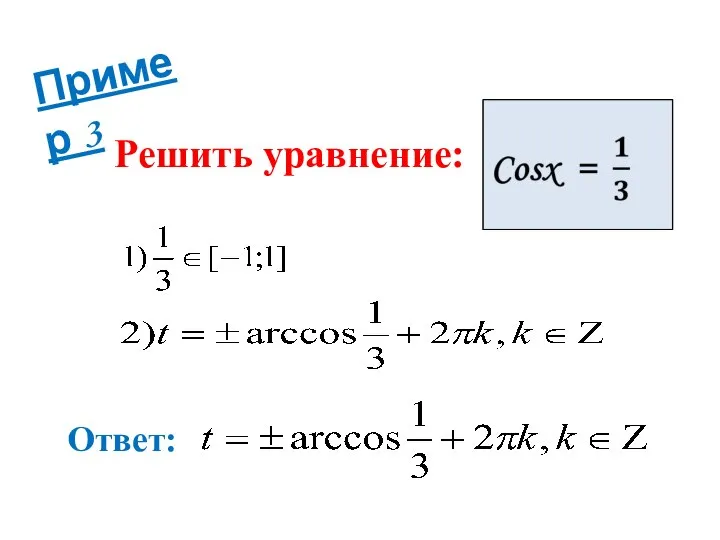
- 17. Пример 3 Решить уравнение: Ответ:
- 18. Частные случаи: cos t = 0 cos t = 1 cos t = - 1 0
- 20. Скачать презентацию






 Презентация на тему Число 0. Цифра 0
Презентация на тему Число 0. Цифра 0  Статистическая теория радиотехнических систем. Вероятностные характеристики огибающей и фазы узкополосногонормального процесса
Статистическая теория радиотехнических систем. Вероятностные характеристики огибающей и фазы узкополосногонормального процесса Математическая прогрессия и где её применяют
Математическая прогрессия и где её применяют Знакомство с деятельностью Ивана Грозного, через решение математических задач
Знакомство с деятельностью Ивана Грозного, через решение математических задач Зимующие птицы. Дети 5 лет
Зимующие птицы. Дети 5 лет Аналитическая геометрия в пространстве
Аналитическая геометрия в пространстве Процентное отношение
Процентное отношение Уравнения, содержащие знак модуля
Уравнения, содержащие знак модуля Частные производные второго порядка. Первый и второй дифференциалы. Локальный экстремум
Частные производные второго порядка. Первый и второй дифференциалы. Локальный экстремум Ряды динамики
Ряды динамики Сложение чисел от 1 до 10
Сложение чисел от 1 до 10 Прятки с фигурами
Прятки с фигурами Графики в ОГЭ
Графики в ОГЭ Знаки тригонометрических функций. Формулы сложения
Знаки тригонометрических функций. Формулы сложения Статические характеристики: среднее арифмтическое
Статические характеристики: среднее арифмтическое Многоугольники в нашей жизни
Многоугольники в нашей жизни Действия с числами, записанными в стандартном виде
Действия с числами, записанными в стандартном виде Сумма углов треугольника
Сумма углов треугольника Предел функции
Предел функции Деление отрицательного числа на отрицательное
Деление отрицательного числа на отрицательное Презентация на тему Действия с натуральными числами и их свойства
Презентация на тему Действия с натуральными числами и их свойства 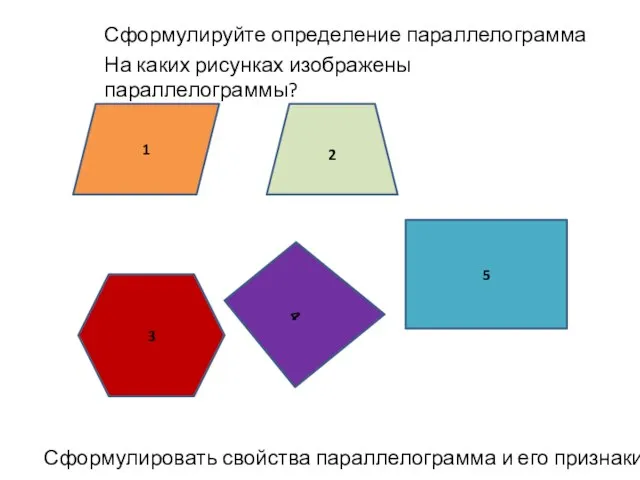 Презентация на тему Параллелограмм и трапеция (8 класс)
Презентация на тему Параллелограмм и трапеция (8 класс)  Центральная и осевая симметрия
Центральная и осевая симметрия Первое знакомство с понятием вероятность. Урок 146
Первое знакомство с понятием вероятность. Урок 146 Квадрат. Основные свойства квадрата
Квадрат. Основные свойства квадрата Метод обратной матрицы решения систем линейных уравнений
Метод обратной матрицы решения систем линейных уравнений Восстанови ряд чисел
Восстанови ряд чисел Четырёхугольник
Четырёхугольник