Содержание
- 2. Цель Задачи Выявление преимуществ геометрических и графических методов решения алгебраических задач. Систематизировать теоретический материал, используемый при
- 3. Гипотеза Объект исследования: алгебраические задачи, текстовые задачи Предмет исследования: изучение геометрических и графических методов решения задач
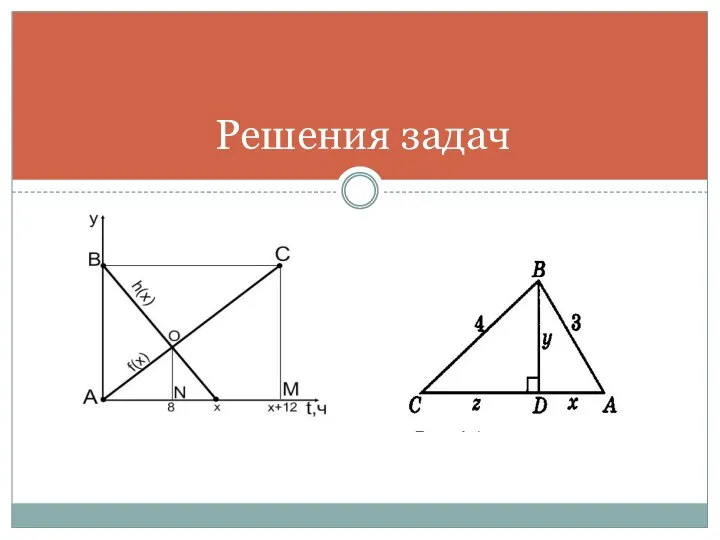
- 4. Решения задач
- 5. Задача 1
- 6. Задача 1
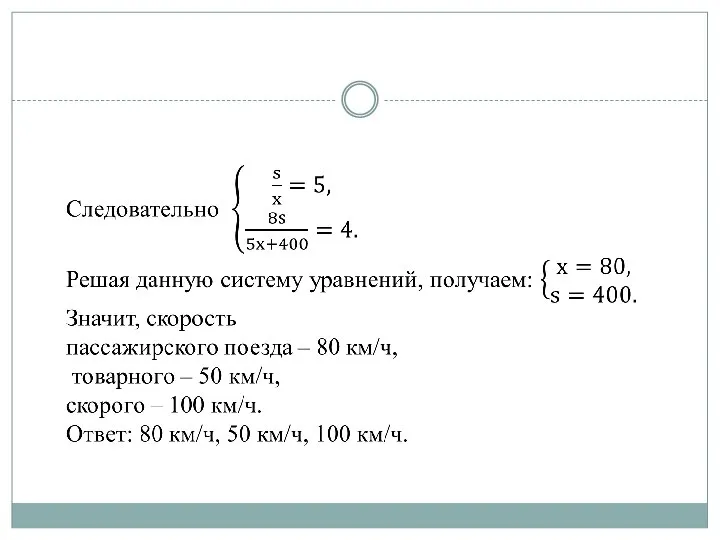
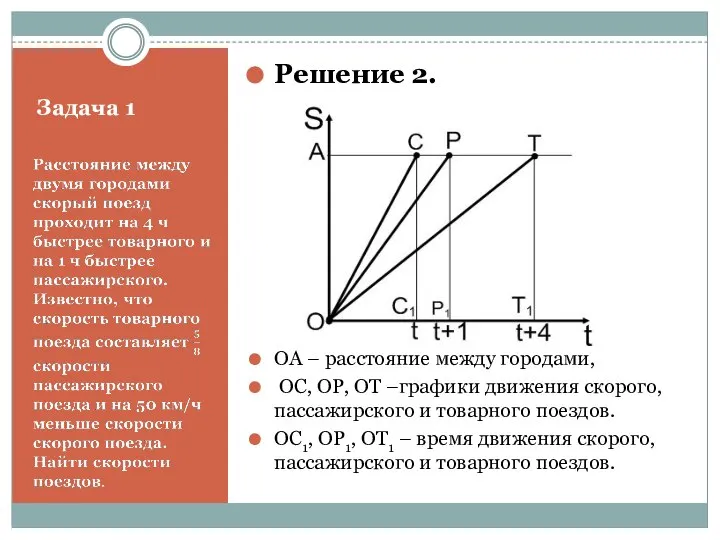
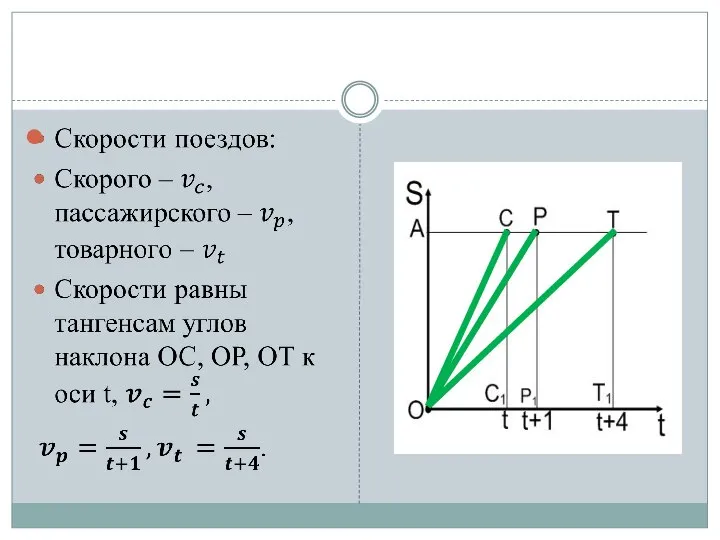
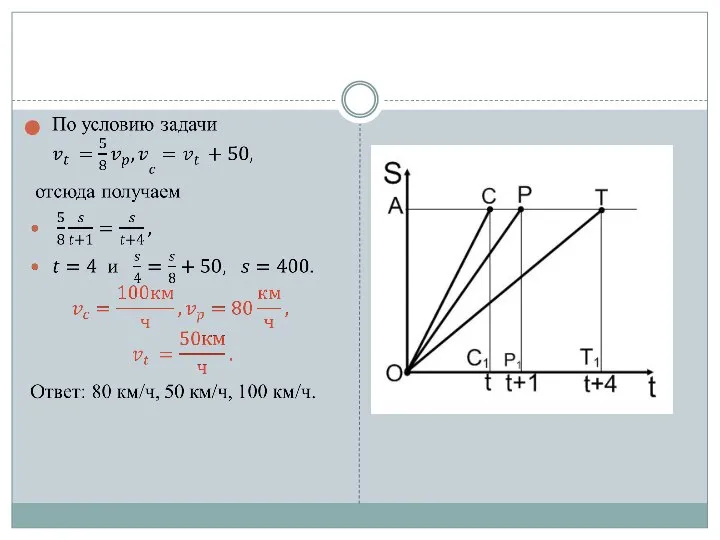
- 8. Задача 1 Решение 2. ОА – расстояние между городами, ОС, ОР, ОТ –графики движения скорого, пассажирского
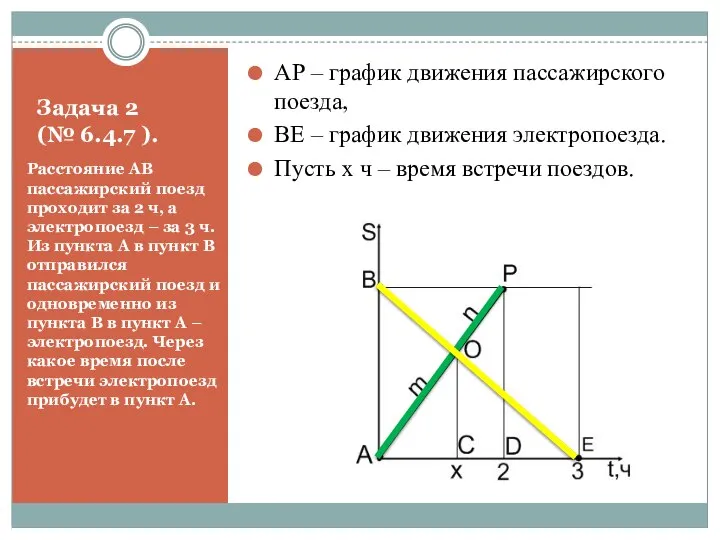
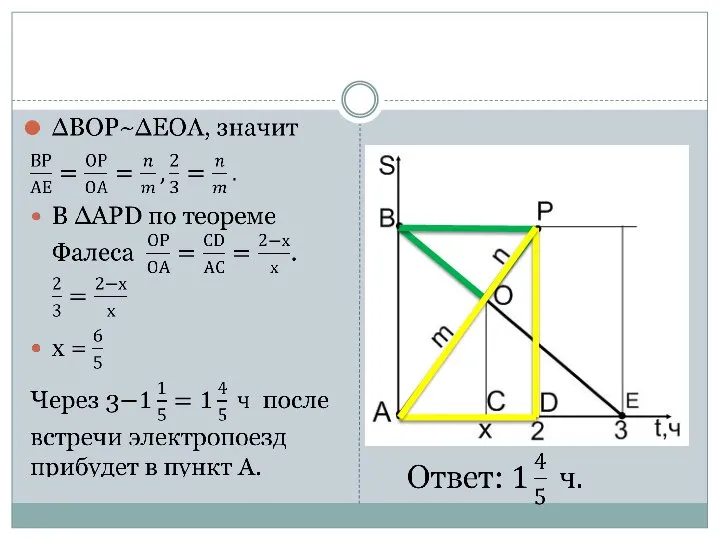
- 11. Задача 2 (№ 6.4.7 ). Расстояние АВ пассажирский поезд проходит за 2 ч, а электропоезд –
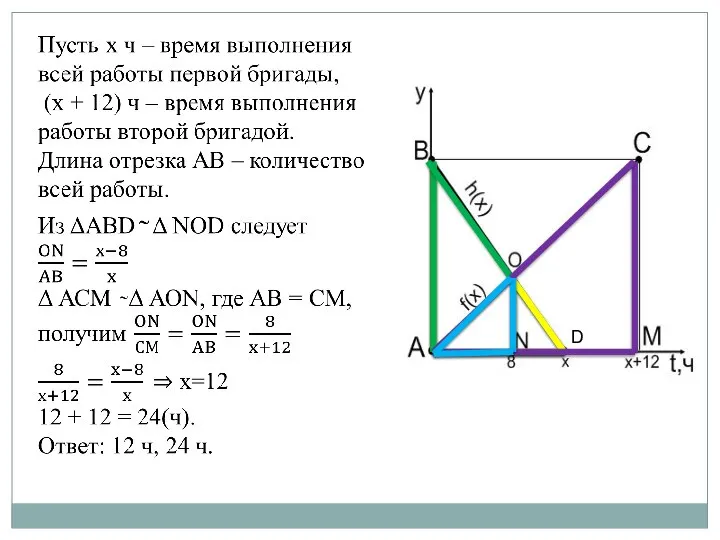
- 13. Задача 3 (№ 6.4.34 ). Две бригады, работая вместе, вспахали поле за 8 ч. За сколько
- 14. D
- 15. Заключение ПРИ РЕШЕНИИ ТЕКСТОВЫХ ЗАДАЧ НА ДВИЖЕНИЕ МОЖНО ПОСТРОИТЬ ГРАФИКИ ДВИЖЕНИЯ (КАК ГРАФИКИ ЛИНЕЙНЫХ ФУНКЦИЙ) И
- 17. Скачать презентацию




 Второй признак равенства треугольников. Урок 16
Второй признак равенства треугольников. Урок 16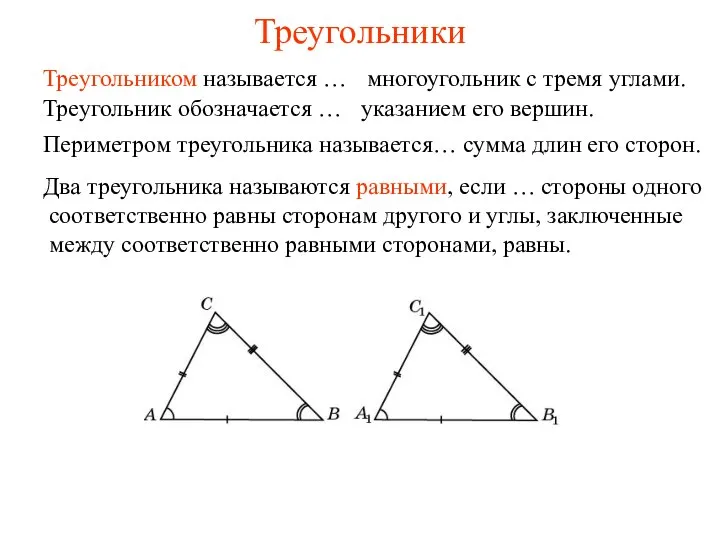 Треугольники
Треугольники График линейной функции
График линейной функции Показательные уравнения
Показательные уравнения Косинус острого угла прямоугольного треугольника
Косинус острого угла прямоугольного треугольника Вычисление площадей плоских фигур. Справочник
Вычисление площадей плоских фигур. Справочник Методы измерения физических величин
Методы измерения физических величин Интегрирование иррациональных выражений
Интегрирование иррациональных выражений Основные элементы комбинаторики и бином Ньютона. Тема 11.1
Основные элементы комбинаторики и бином Ньютона. Тема 11.1 Теорема Пифагора
Теорема Пифагора Решение систем неравенств
Решение систем неравенств Единицы объёма. Задания
Единицы объёма. Задания Сумма углов треугольника. Виды треугольников
Сумма углов треугольника. Виды треугольников Определение параметров закона распределения результатов измерений по статистическим критериям
Определение параметров закона распределения результатов измерений по статистическим критериям Свойства касательной
Свойства касательной Числовая окружность
Числовая окружность Поиск сокровищ. Изучений геометрических фигур
Поиск сокровищ. Изучений геометрических фигур Монотонность, экстремумы
Монотонность, экстремумы Тренажер. Примеры
Тренажер. Примеры Teorema_polnoy_veroyatnosti
Teorema_polnoy_veroyatnosti Решение задач. Штрих Шеффера
Решение задач. Штрих Шеффера Понятие композиции отношений. Виды отношений
Понятие композиции отношений. Виды отношений Геометрический биатлон
Геометрический биатлон Вычисление интегралов вида R(x, Jax2 + bx+c) dx
Вычисление интегралов вида R(x, Jax2 + bx+c) dx Рациональные дроби и их свойства
Рациональные дроби и их свойства Построение таблиц истинности
Построение таблиц истинности Логарифмические уравнения
Логарифмические уравнения Вычисления и преобразования
Вычисления и преобразования