Решение задач, возникающих в реальной жизни, с использованием теоретико-множественного подхода

Примеры операций над множествами

Задание из ЕГЭ (Германия)
Формулировка задачи:
В классе 20 учеников, из которых 12 изучают биологию, 15 - историю и 2 не изучают ни биологию, ни историю. Сколько учеников изучает и биологию и историю?
Ответ: 9

Основные тождества теории множеств
Коммутативность объединения и пересечения А ∪ В = В ∪ А; А ∩ В = В ∩ А
Дистрибутивность объединения и пересечения
(А ∪ В) ∪ С = А ∪ (В ∪ С); ( А ∩ В) ∩ С = А ∩ (В ∩ С)
Взаимная дистрибутивность объединения и пересечения
(А ∪ В) ∩ С = (А ∩ В) ∪ (В ∩ С); (А ∩ В) ∪ С = (А ∪ В) ∩ (В ∪ С)
Формальное доказательство взаимной дистрибутивности (1-го тождества)
Пусть x ∈ (А ∪ В) ∩ С Тогда x ∈ А ∪ В и x ∈ С
Значит, x принадлежит хотя бы одному из множеств А; В и принадлежит С
Тогда x принадлежит хотя бы одному из множеств А ∩ С; В ∩ С
Значит, x принадлежит правой части тождества
Доказали ли мы формулу?
НЕТ!
В обратную сторону устно.
Геометрическое доказательство:
Принцип двойственности
S \ (А1 ∪ A2) = (S \ A1) ∩ (S \ A2)
S \ (А1 ∩ A2) = (S \ A1) ∪ (S \ A2)

Отображения множеств
Отображение ƒ: А → В - это правило, которое каждому
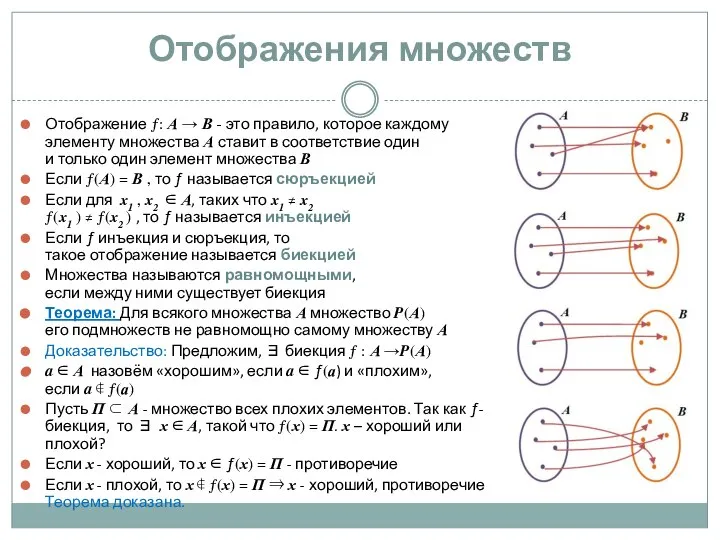
элементу множества А ставит в соответствие один
и только один элемент множества В
Если ƒ(А) = В , то ƒ называется сюръекцией
Если для x1 , x2 ∈ А, таких что x1 ≠ x2
ƒ(x1 ) ≠ ƒ(x2 ) , то ƒ называется инъекцией
Если ƒ инъекция и сюръекция, то
такое отображение называется биекцией
Множества называются равномощными,
если между ними существует биекция
Теорема: Для всякого множества А множество P(А)
его подмножеств не равномощно самому множеству А
Доказательство: Предложим, ∃ биекция ƒ : А →P(А)
a ∈ А назовём «хорошим», если a ∈ ƒ(а) и «плохим»,
если a ∉ ƒ(а)
Пусть П ⊂ А - множество всех плохих элементов. Так как ƒ- биекция, то ∃ х ∈ А, такой что ƒ(х) = П. х – хороший или плохой?
Если х - хороший, то х ∈ ƒ(х) = П - противоречие
Если х - плохой, то х ∉ ƒ(х) = П ⇒ х - хороший, противоречие
Теорема доказана.

Счётность ℚ и несчётность ℝ
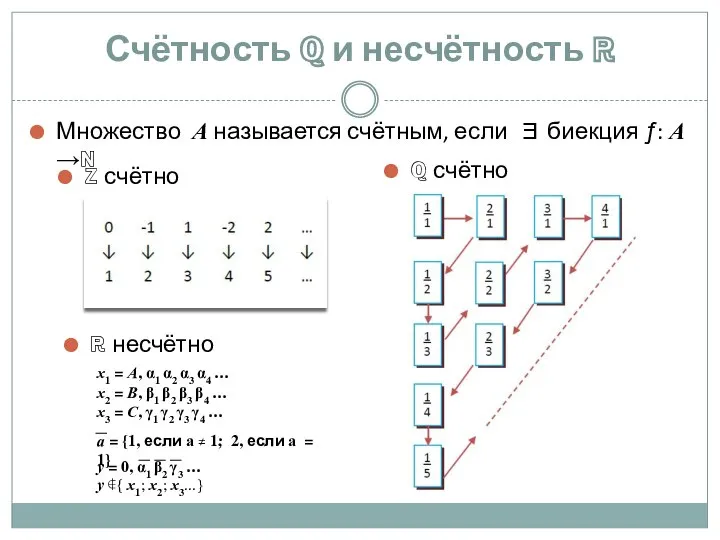
Множество А называется счётным, если ∃ биекция ƒ: А →ℕ