Системы обыкновенных дифференциальных уравнений

Дана система n уравнений с n неизвестными функциями
Нормальная система дифференциальных уравнений (1) называется линейной, если функции , входящие в правые части, линейны относительно неизвестных функций :
(3)

Система (3) называется неоднородной, если хотя бы одна из функций не равна тождественно нулю.
Система (3) называется однородной, если все функции

Запись системы (3) в матричной форме.
Обозначим
Коротко:

Линейные однородные системы с постоянными коэффициентами
Пусть в системе (3) все коэффициенты постоянны и .
(4)
Или в векторной форме .
Какой вид имеет общее решение системы ( 4)?

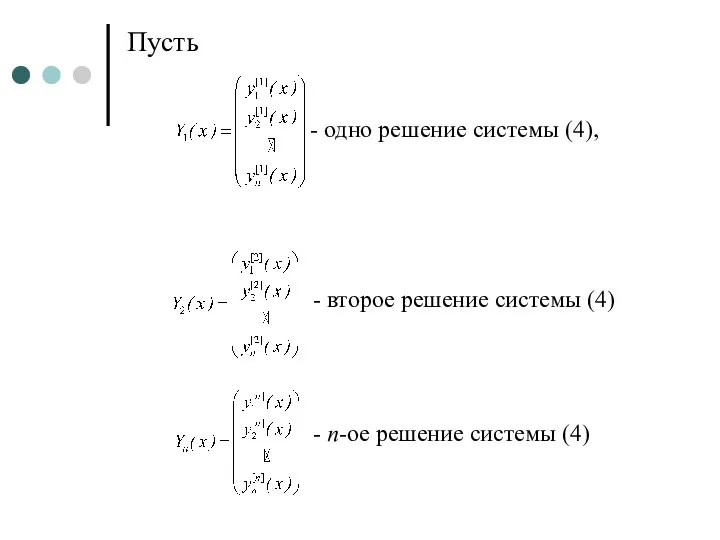
Пусть
- одно решение системы (4),
- второе решение системы (4)
- n-ое решение системы (4)

Определитель Вронского системы решений
В случае системы определителем Вронского для функций называется:
Система решений образует ФСР на
[a;b], если

Теорема о структуре общего решения системы
Если решения образуют ФСР, то общее решение этой системы находится по формуле:
, где
произвольные постоянные.

Пусть n = 3
(5)
Решаем (5) методом Эйлера. Ищем частное решение в виде:
Определим постоянные так, чтобы
было решением системы (5):

После подстановки в (5) получим
следующую систему:
или
(6)
Это система линейных однородных алгебраических уравнений относительно неизвестных имеет ненулевые решения, если ее основной определитель равен нулю:

То есть
получаем характеристическое уравнение системы (5):
Получим уравнение третьей степени относительно k. Значит оно имеет 3 корня, действительных или комплексных, простых или кратных.

Первый случай: корни характеристического уравнения действительные и различные.
В этом случае мы получаем три следующих частных решения системы (5):
При этом найдем значения постоянных как
решение системы (6), полагая последовательно
.

Можно показать, что .
Следовательно, образуют фундаментальную систему решений для (5), и тогда общее решение системы (5) будет:
.
Или подробнее

Пример (первый способ)

Пример (второй способ)
Дана та же система дифференциальных уравнений
. Ищем решение в виде:

Общее решение:
По теореме о структуре общего решения
Пусть тогда

Случай комплексных корней характеристического уравнения
Пусть корни характеристического уравнения - комплексно-сопряженные.
Y и заменим на пару действительных решений:
и

Пример

Выделяем действительную и мнимую части
Получим:
Общее решение: значит

Кратные корни характеристического уравнения
Например, корень характеристического уравнения имеет кратность 3, то решение нужно искать в виде:
Числа находятся
методом неопределенных
коэффициентов.

Пример
Дана система двух уравнений:
, характеристическое уравнение:
Ищем решение системы в виде:
Найдем производные и подставим в данную систему:

Разделим на
Получим:
Приравняем коэффициенты при x :
Приравняем коэффициенты при :

Получаем систему:
2 уравнения с 4-мя неизвестными, 2 из них являются свободными. Пусть тогда
Ответ:

Неоднородные системы дифференциальных уравнений
Найти общее решение:
(1)
Соответствующая однородная система:
Ее общее решение: .
Подставляем эти значения в (1), считая неизвестными функциями x.

После приведения, получим систему:
Решая ее относительно и затем интегрируя, получим