Содержание
- 2. Окружность и круг Окружностью называется геометрическая фигура, состоящая из всех точек плоскости, расположенных на заданном расстоянии
- 3. Определение сферы Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии (R) от
- 4. Шар Шаром называется тело, ограниченное сферой. Центр, радиус и диаметр сферы являются также центром, радиусом и
- 5. Уравнение окружности О С(х0;у0) М(х;у) Уравнение окружности: (x – x0)2 + (y – y0)2 = r2
- 6. Уравнение сферы Зададим прямоугольную систему координат Оxyz z х у М(х;у;z) R C(x0;y0;z0) МС = (x
- 7. Задача 1. Зная координаты центра С(2;-3;0) и радиус сферы R=5, записать уравнение сферы. Ответ: (x-2)2 +
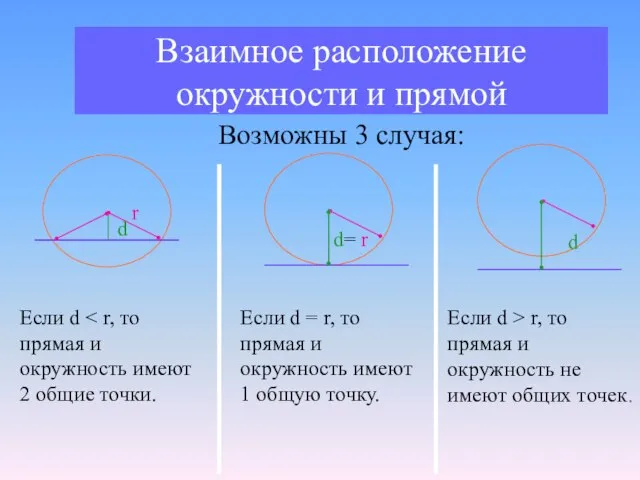
- 8. Взаимное расположение окружности и прямой Возможны 3 случая: d d r Если d d= r Если
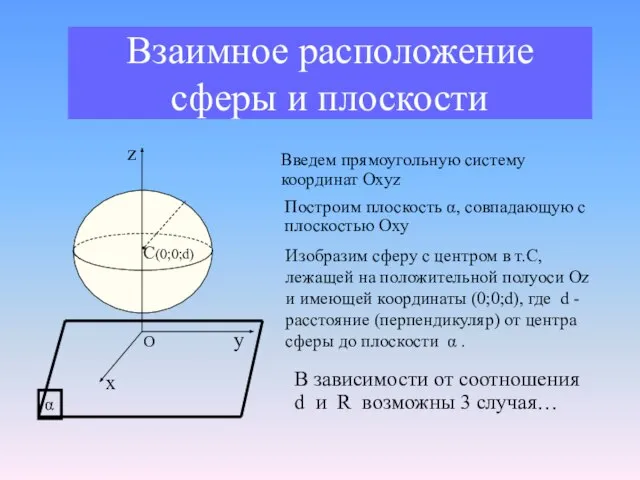
- 9. Взаимное расположение сферы и плоскости Введем прямоугольную систему координат Oxyz Построим плоскость α, совпадающую с плоскостью
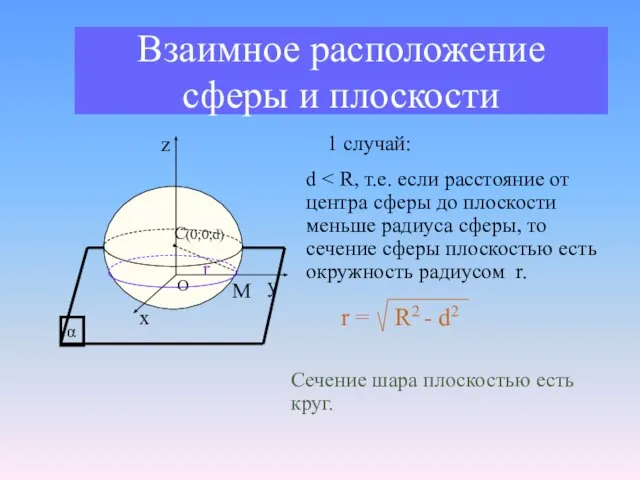
- 10. Взаимное расположение сферы и плоскости r М 1 случай: d r = R2 - d2 Сечение
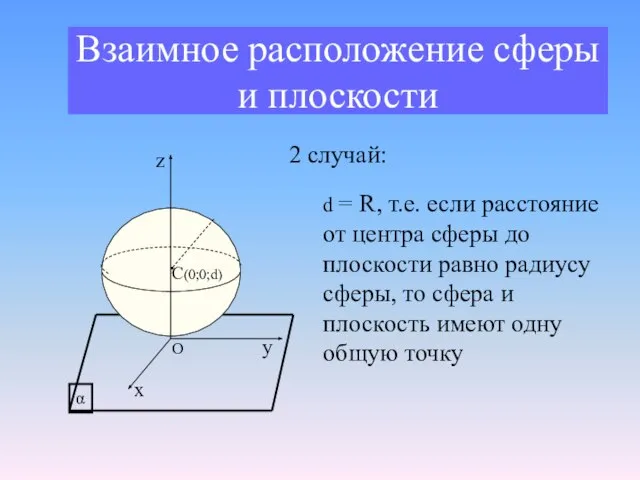
- 11. Взаимное расположение сферы и плоскости 2 случай: d = R, т.е. если расстояние от центра сферы
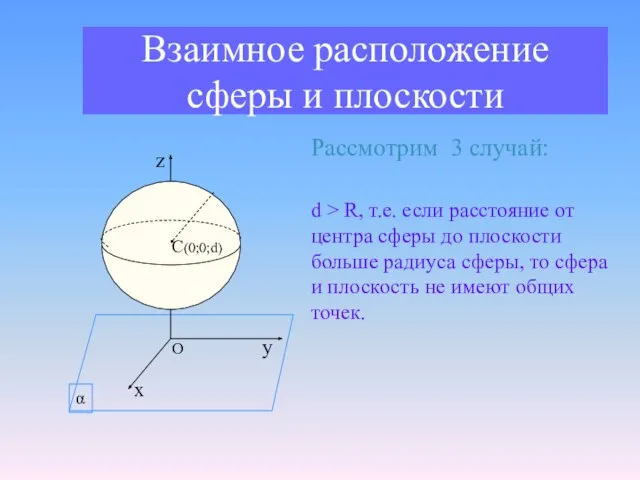
- 12. Взаимное расположение сферы и плоскости Рассмотрим 3 случай: d > R, т.е. если расстояние от центра
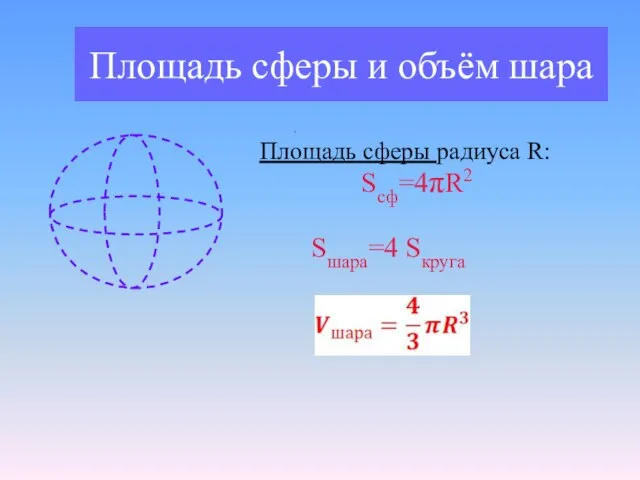
- 13. Площадь сферы и объём шара . Площадь сферы радиуса R: Sсф=4πR2 Sшара=4 Sкруга
- 14. Радиусы трех шаров равны 6, 8 и 10. Найдите радиус шара, объем которого равен сумме их
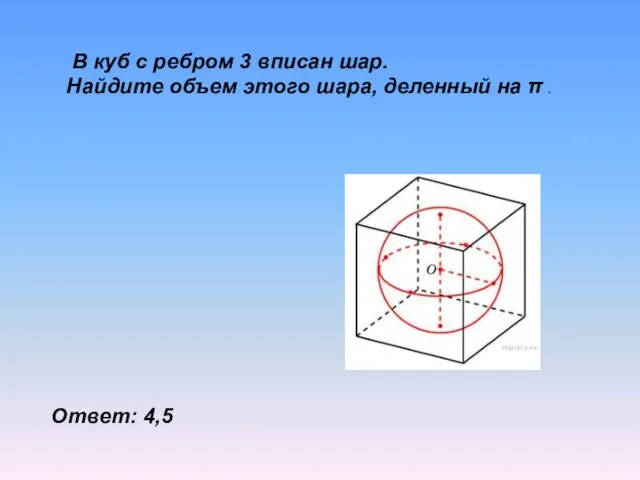
- 15. В куб с ребром 3 вписан шар. Найдите объем этого шара, деленный на π . Ответ:
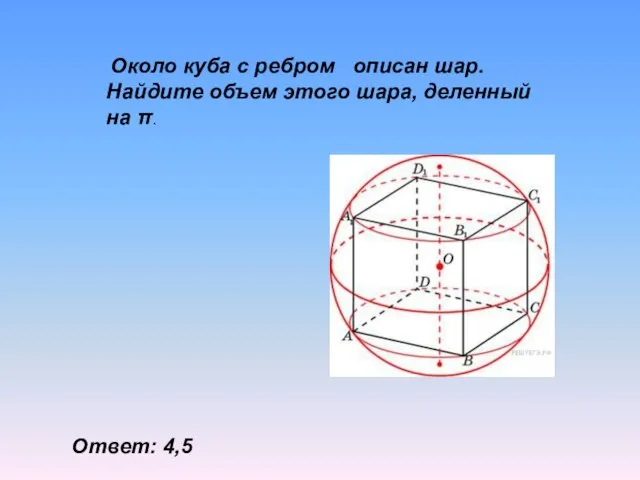
- 16. Около куба с ребром описан шар. Найдите объем этого шара, деленный на π. Ответ: 4,5
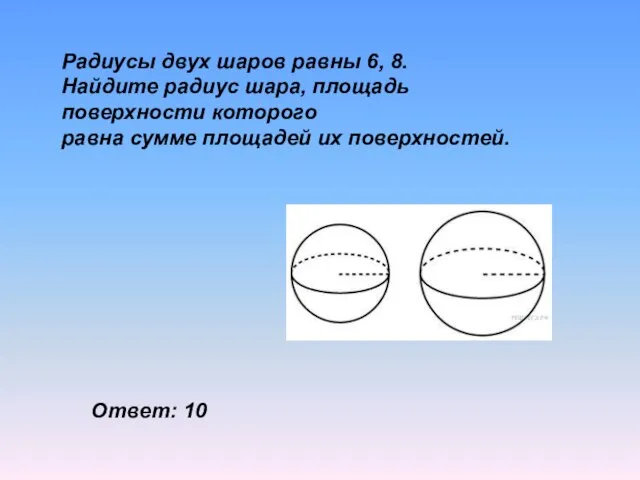
- 17. Радиусы двух шаров равны 6, 8. Найдите радиус шара, площадь поверхности которого равна сумме площадей их
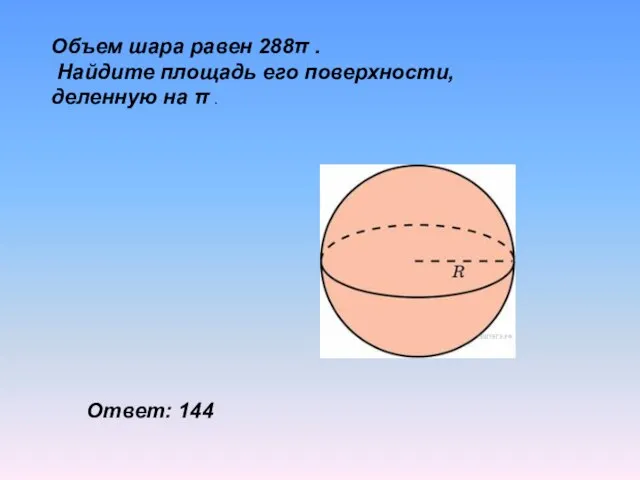
- 18. Объем шара равен 288π . Найдите площадь его поверхности, деленную на π . Ответ: 144
- 19. Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем конуса равен 6. Найдите объем
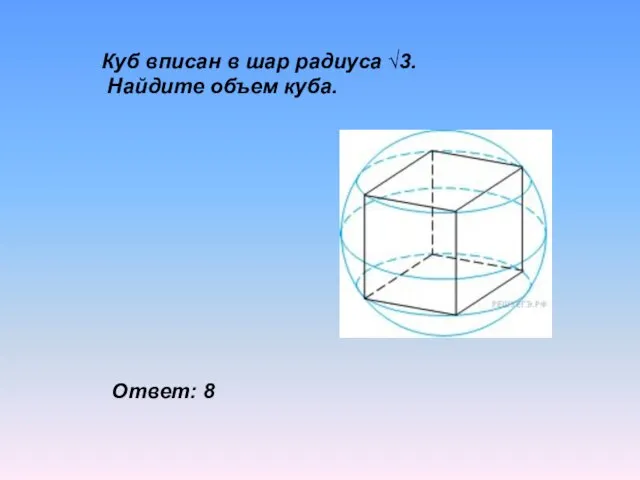
- 20. Куб вписан в шар радиуса √3. Найдите объем куба. Ответ: 8
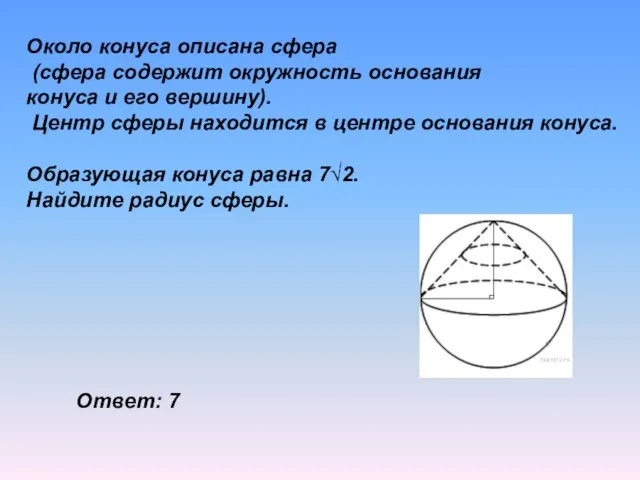
- 21. Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы находится в
- 22. Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы находится в
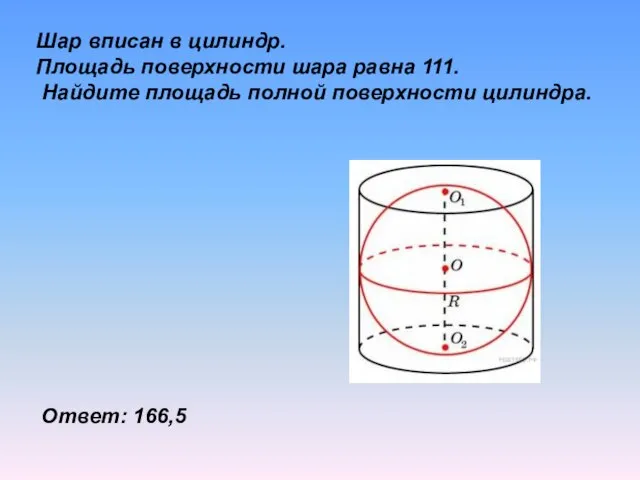
- 23. Шар вписан в цилиндр. Площадь поверхности шара равна 111. Найдите площадь полной поверхности цилиндра. Ответ: 166,5
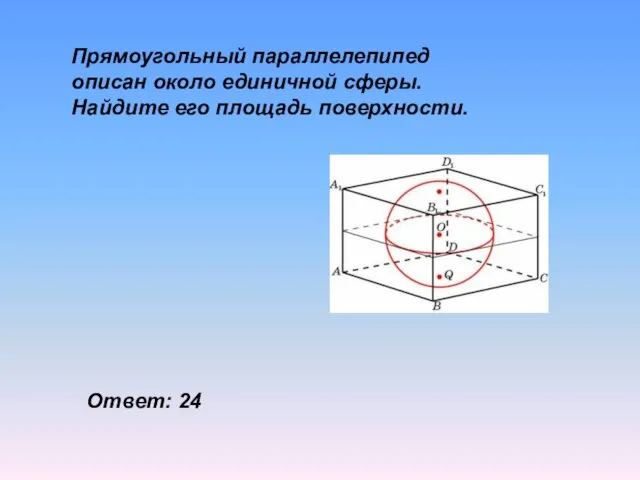
- 24. Прямоугольный параллелепипед описан около единичной сферы. Найдите его площадь поверхности. Ответ: 24
- 25. Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем шара равен 28. Найдите объем
- 26. Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем конуса равен 6. Найдите объем
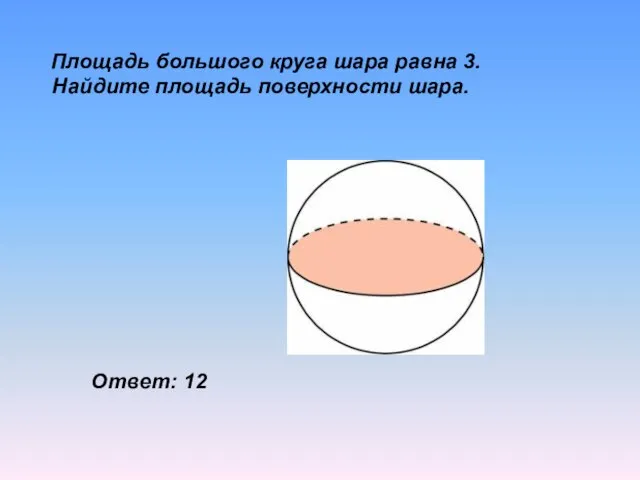
- 27. Площадь большого круга шара равна 3. Найдите площадь поверхности шара. Ответ: 12
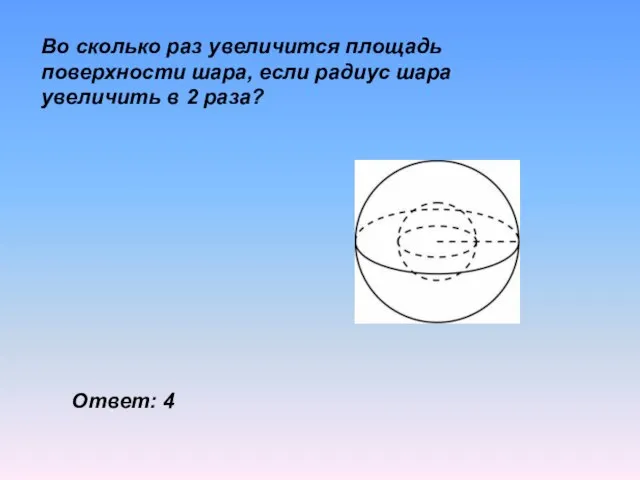
- 28. Во сколько раз увеличится площадь поверхности шара, если радиус шара увеличить в 2 раза? Ответ: 4
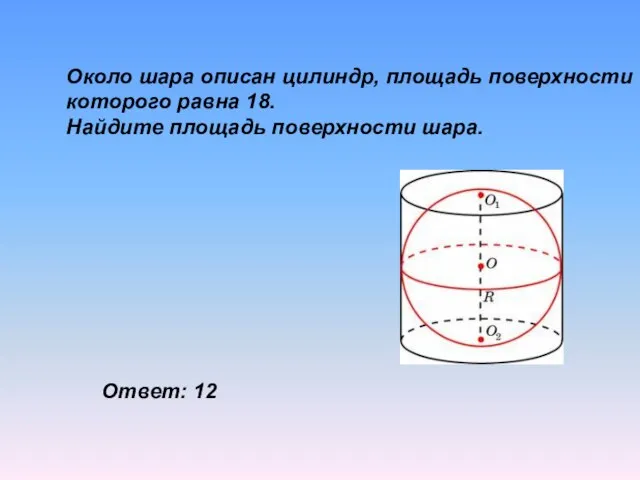
- 29. Около шара описан цилиндр, площадь поверхности которого равна 18. Найдите площадь поверхности шара. Ответ: 12
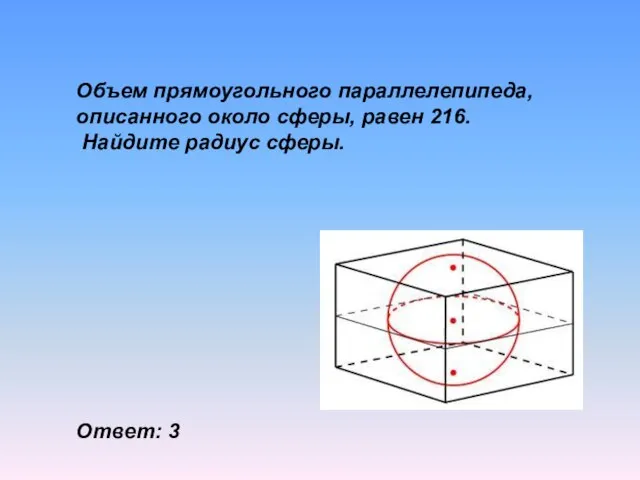
- 30. Объем прямоугольного параллелепипеда, описанного около сферы, равен 216. Найдите радиус сферы. Ответ: 3
- 32. Скачать презентацию











 Вероятность, статистика и функциональная грамотность в итоговой и промежуточной аттестации по математике
Вероятность, статистика и функциональная грамотность в итоговой и промежуточной аттестации по математике Сколько раз в день минутная и часовая стрелки образуют прямую линию?
Сколько раз в день минутная и часовая стрелки образуют прямую линию? Уравнение окркжности
Уравнение окркжности Таблицs истинности
Таблицs истинности Что называется обыкновенной дробью?
Что называется обыкновенной дробью? Задачи на умножение и деление и опорные схемы к ним. Опорные схемы задач 3 класс
Задачи на умножение и деление и опорные схемы к ним. Опорные схемы задач 3 класс Квадратичная функция
Квадратичная функция Учимся писать цифры
Учимся писать цифры Предельные теоремы ТВ
Предельные теоремы ТВ Условия с логическими связками. Задачи
Условия с логическими связками. Задачи Разложение многочлена на множители
Разложение многочлена на множители Дополни до 10
Дополни до 10 Перестановки. Размещения
Перестановки. Размещения Цилиндр
Цилиндр Деление обыкновенных дробей
Деление обыкновенных дробей Определённый интеграл. 11 класс
Определённый интеграл. 11 класс Уравнение окружности
Уравнение окружности Статистика
Статистика Презентация на тему Теорема косинусов
Презентация на тему Теорема косинусов  Применение производной
Применение производной Бастапқы математикалық көріністерді қалыптастыру
Бастапқы математикалық көріністерді қалыптастыру Презентация на тему ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМОЙ И ПЛОСКОСТИ
Презентация на тему ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМОЙ И ПЛОСКОСТИ  Окружность
Окружность Первый признак подобия треугольников. 8 класс
Первый признак подобия треугольников. 8 класс Десятки и единицы
Десятки и единицы Задачи краеведческого содержания
Задачи краеведческого содержания Веселая математика
Веселая математика Методы решения систем линейных уравнений: метод сложения
Методы решения систем линейных уравнений: метод сложения