Основы построения цифровых автоматов и систем анализа информационных процессов. Понятия СДНФ и СКНФ. Логико-вероятностное
Содержание
- 2. Введение Многие важные научные и технические направления, такие как геофизика, радио и гидролокация, метеорология, обработка изображений,
- 3. Математическая ( символическая ) логика с развитием вычислительной техники (ВТ) оказалась в тесной взаимосвязи с вычислительной
- 4. У истоков современной логики цифровых автоматов стоит Г. Лейбниц ( из Германии, 1646-1716 гг. ), выдвинувший
- 5. Решающий шаг в области математической логики был сделан Дж. Булем (1815-1864) – алгебры логики (1847). Алгебра
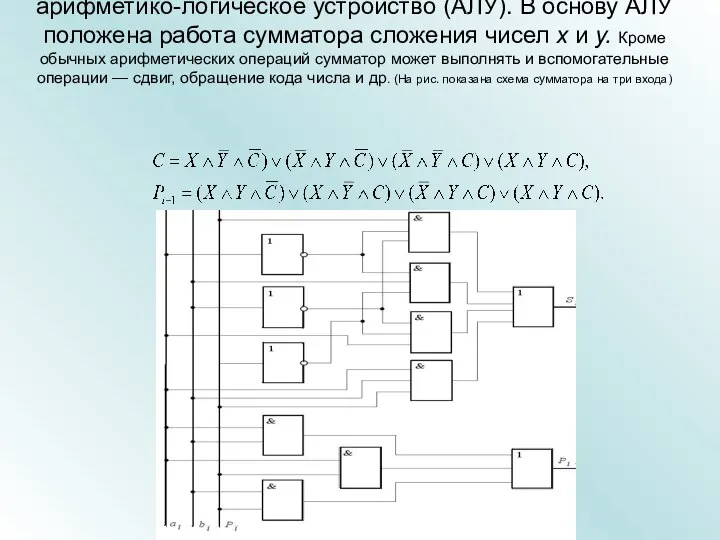
- 6. Одна из главных составных частей цифровой ВС – это арифметико-логическое устройство (АЛУ). В основу АЛУ положена
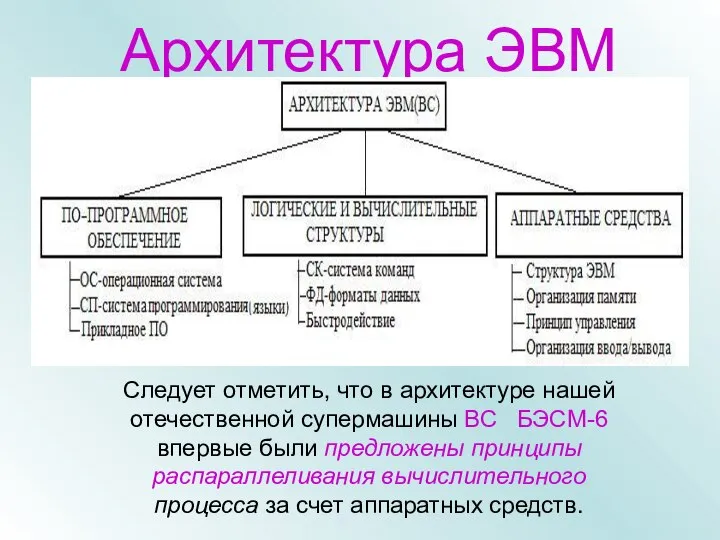
- 7. Архитектура ЭВМ Следует отметить, что в архитектуре нашей отечественной супермашины ВС БЭСМ-6 впервые были предложены принципы
- 8. Базовая структура параллельной ЭВМ Параллельная ЭВМ с общим управлением, ориентированная на решение параллельных вычислительных задач, содержит
- 9. В составе каждого блока ВМ имеются локальные устройства управления (ЛУУ), имеющие память программ и логику управления.
- 10. Ввод программ и данных в параллельную ВС, управление периферией и общее управление все ВС осуществляет управляющая
- 11. Преимущества параллельной обработки информации ВС основаны на том, что в системе с большой размерностью задачи, для
- 12. Анализ множества цифровых ЭВМ и ВС показывает, что их фундамент (базис) – математическая логика. Основы математической
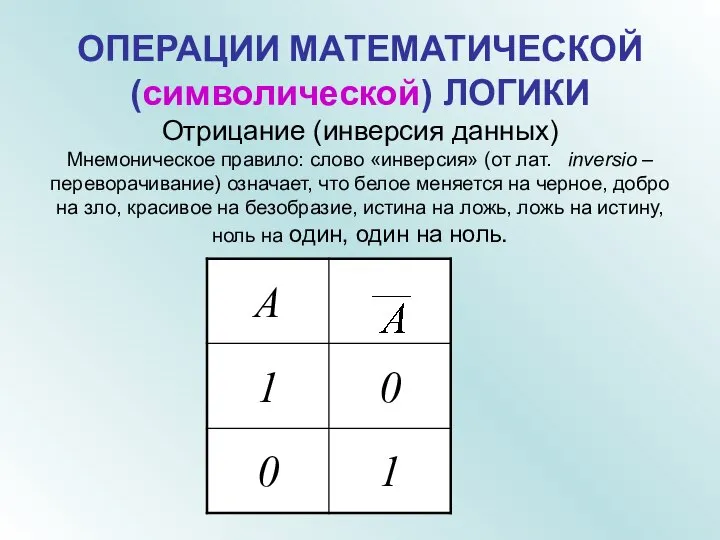
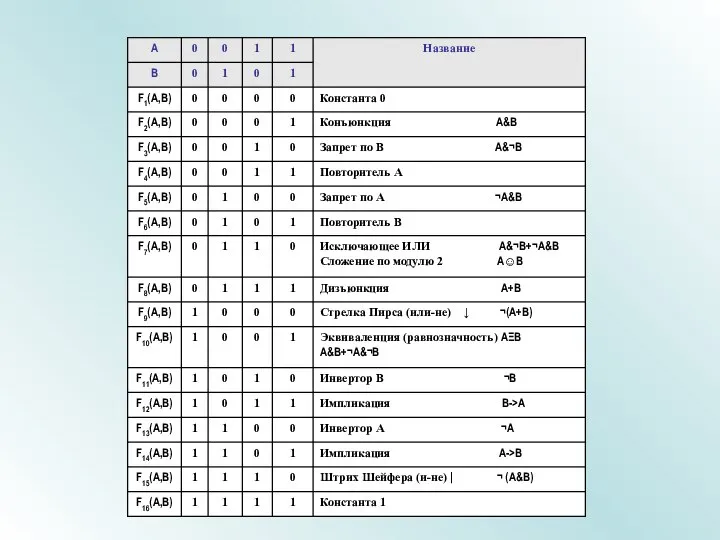
- 13. ОПЕРАЦИИ МАТЕМАТИЧЕСКОЙ (символической) ЛОГИКИ Отрицание (инверсия данных) Мнемоническое правило: слово «инверсия» (от лат. inversio – переворачивание)
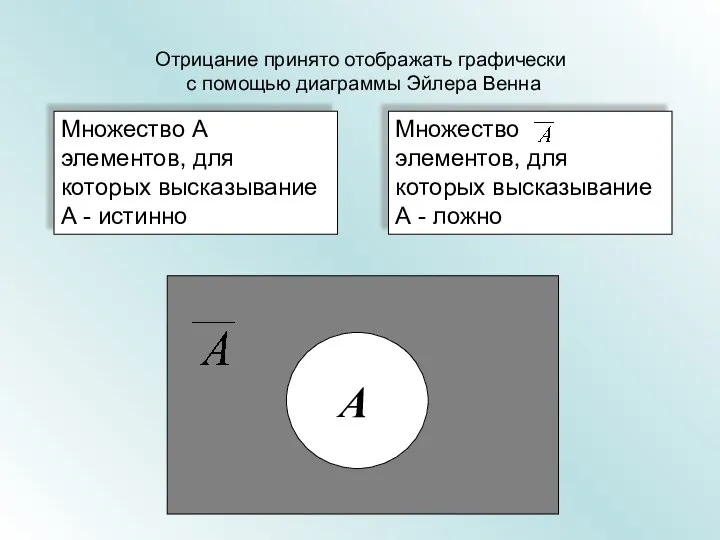
- 14. Множество элементов, для которых высказывание А - ложно Отрицание принято отображать графически с помощью диаграммы Эйлера
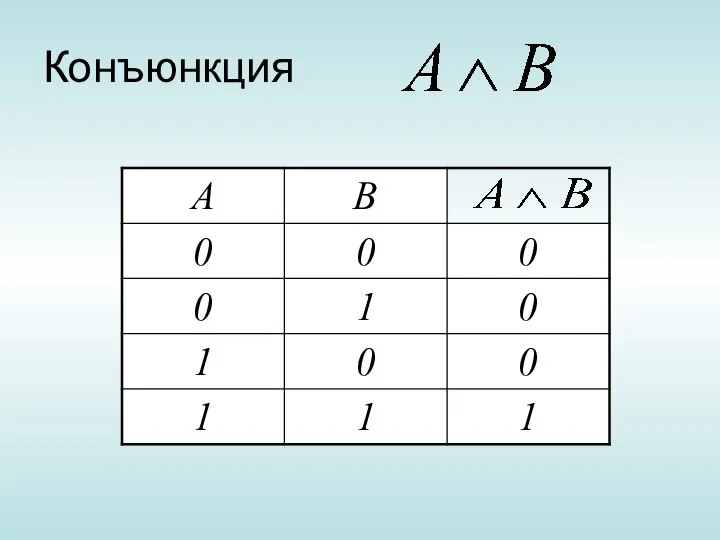
- 15. Конъюнкция
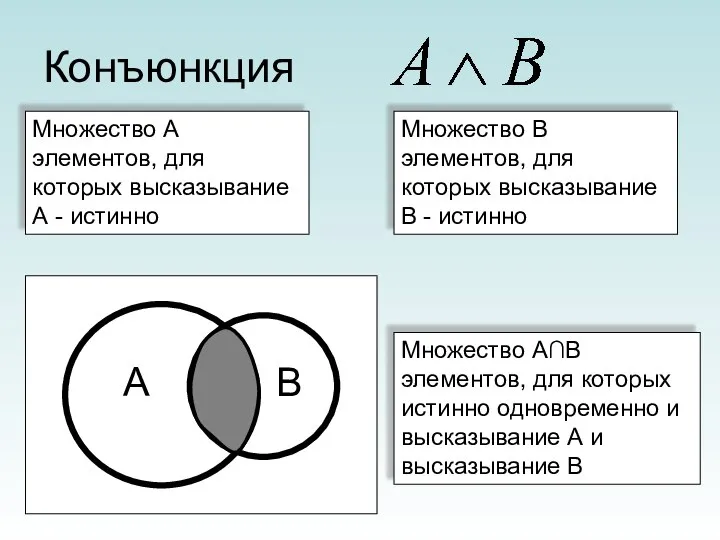
- 16. Конъюнкция Множество А элементов, для которых высказывание А - истинно Множество В элементов, для которых высказывание
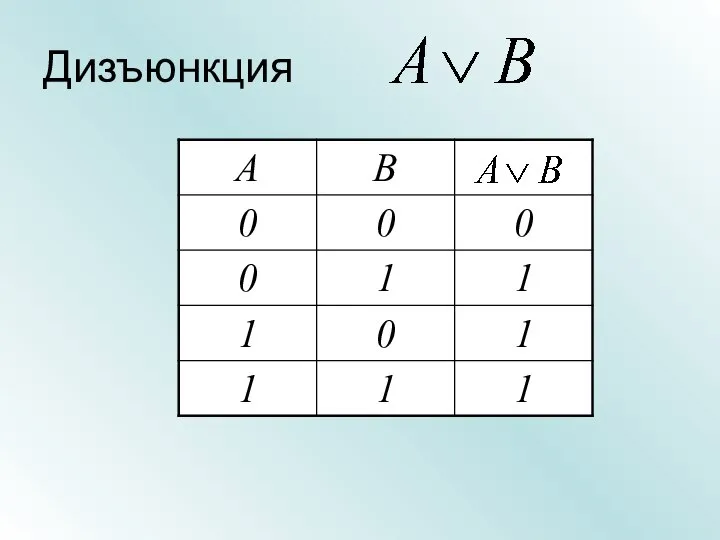
- 17. Дизъюнкция
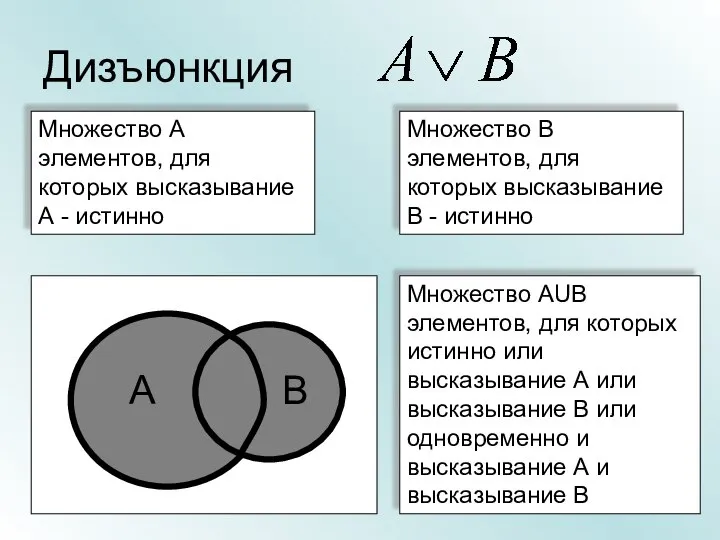
- 18. Дизъюнкция Множество А элементов, для которых высказывание А - истинно Множество В элементов, для которых высказывание
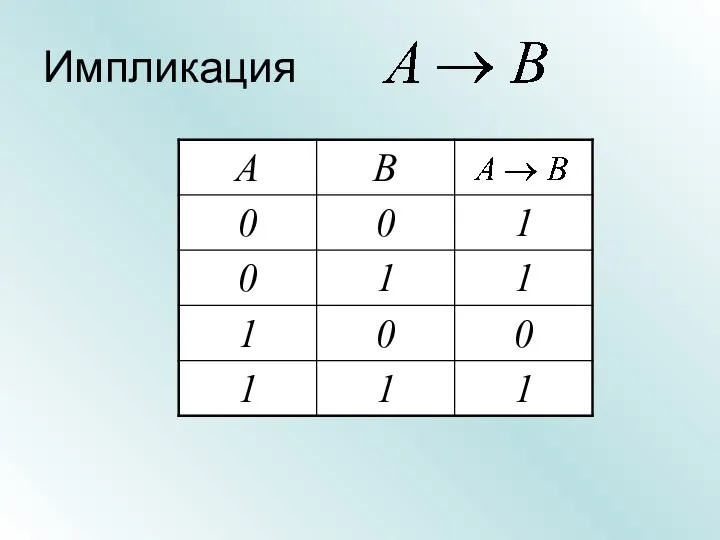
- 19. Импликация
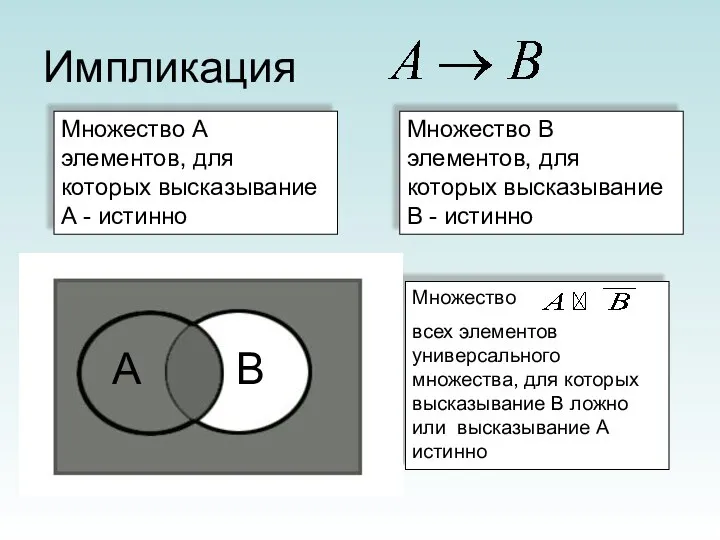
- 20. Импликация Множество А элементов, для которых высказывание А - истинно Множество В элементов, для которых высказывание
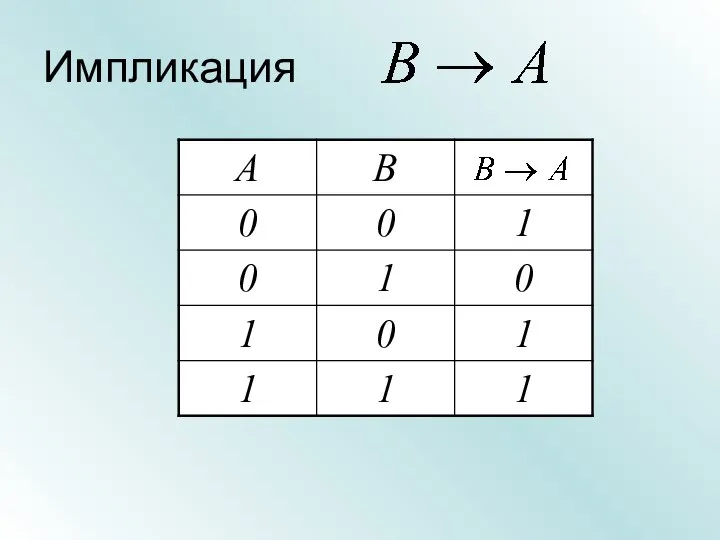
- 21. Импликация
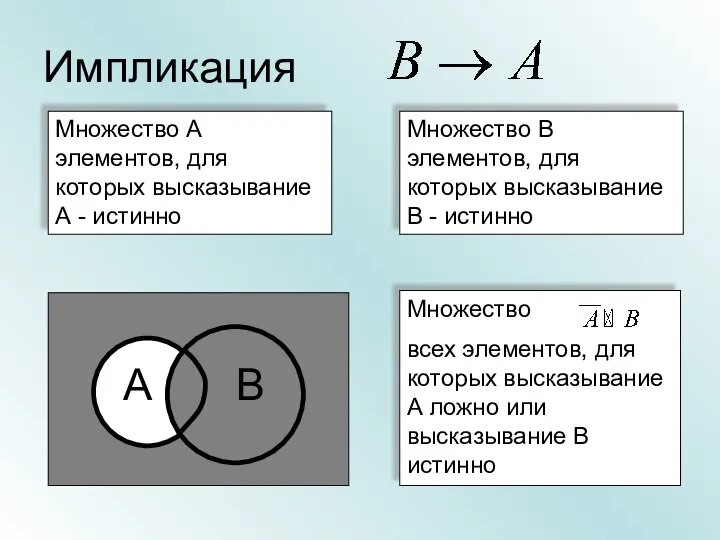
- 22. Импликация Множество А элементов, для которых высказывание А - истинно Множество В элементов, для которых высказывание
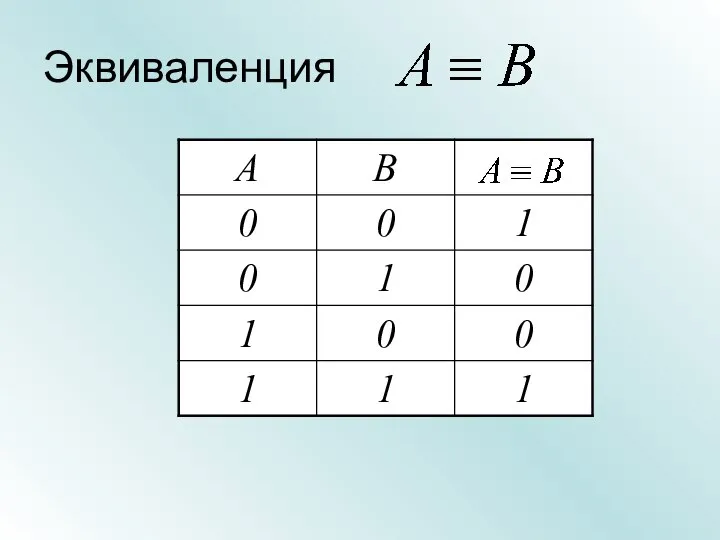
- 23. Эквиваленция
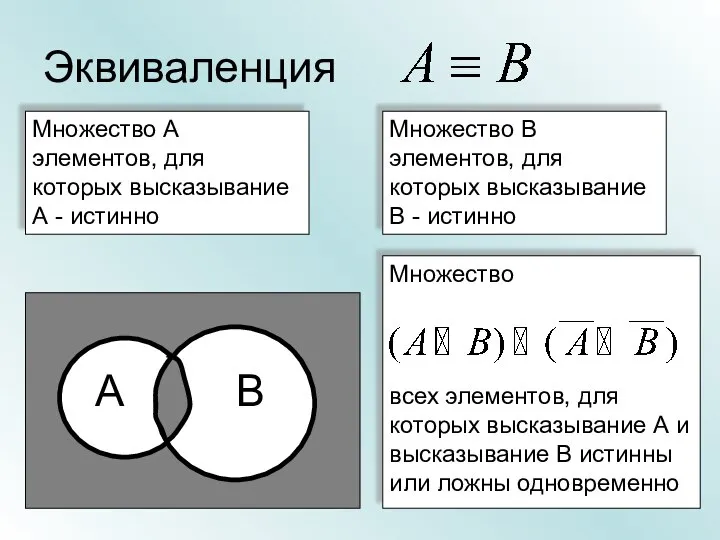
- 24. Эквиваленция Множество А элементов, для которых высказывание А - истинно Множество В элементов, для которых высказывание
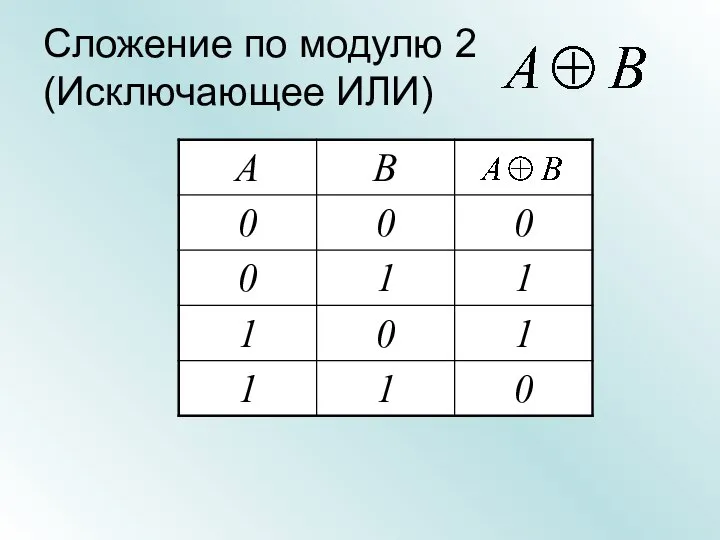
- 25. Сложение по модулю 2 (Исключающее ИЛИ)
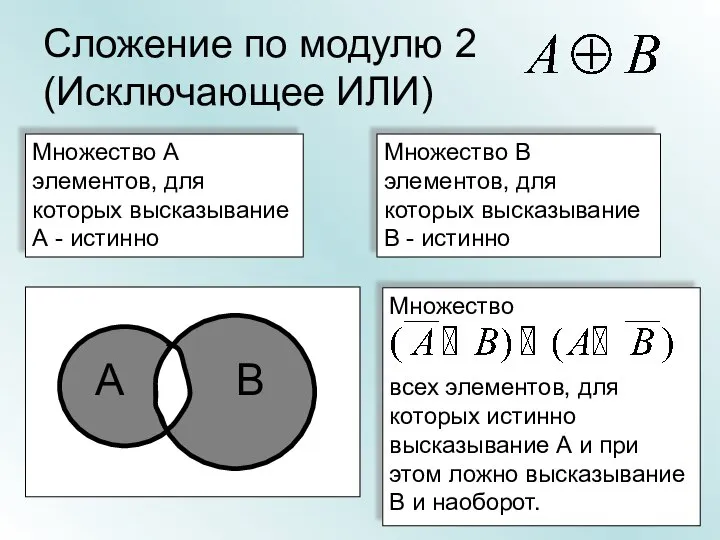
- 26. Сложение по модулю 2 (Исключающее ИЛИ) Множество А элементов, для которых высказывание А - истинно Множество
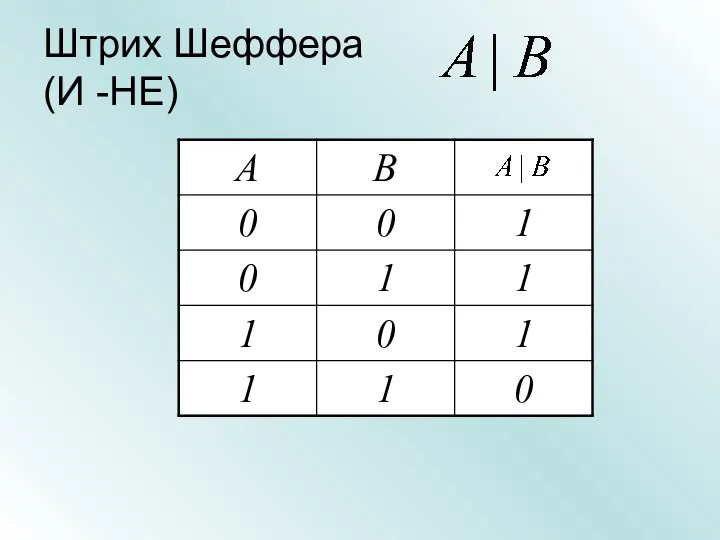
- 27. Штрих Шеффера (И -НЕ)
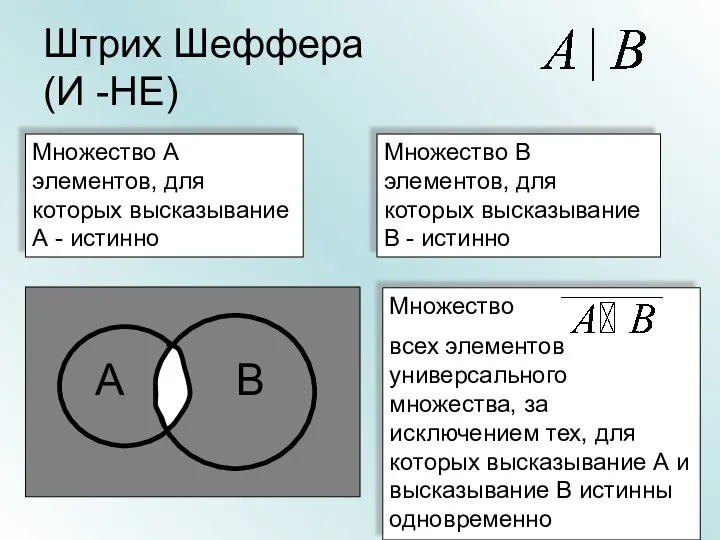
- 28. Штрих Шеффера (И -НЕ) Множество А элементов, для которых высказывание А - истинно Множество В элементов,
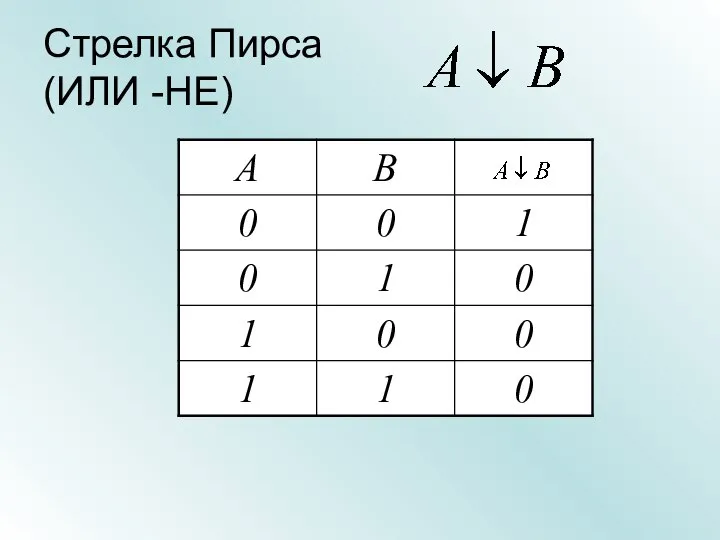
- 29. Стрелка Пирса (ИЛИ -НЕ)
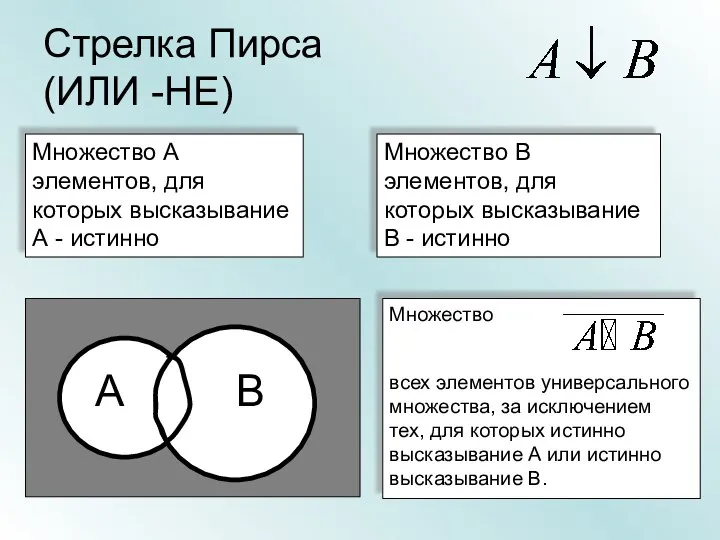
- 30. Стрелка Пирса (ИЛИ -НЕ) Множество А элементов, для которых высказывание А - истинно Множество В элементов,
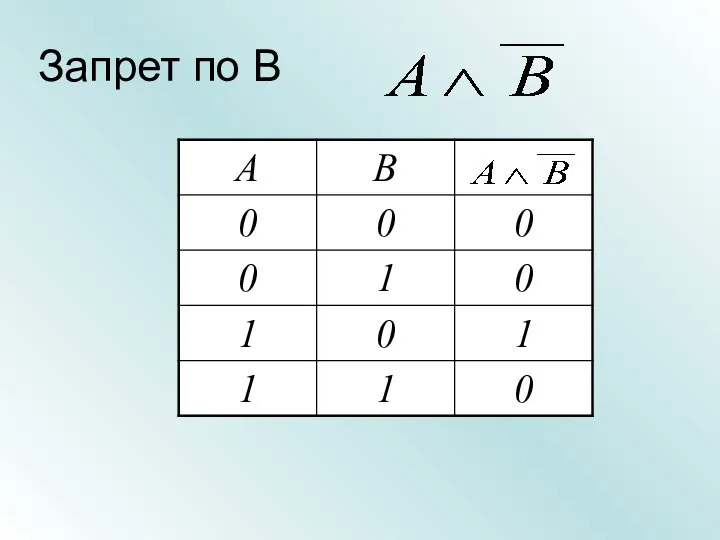
- 31. Запрет по В
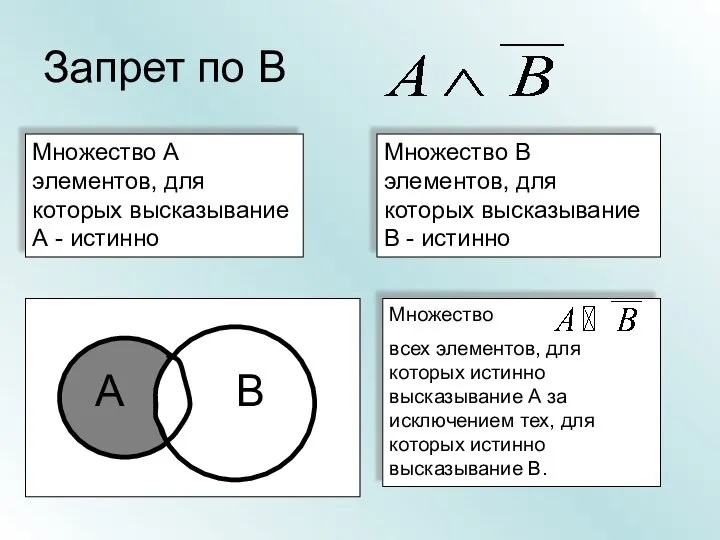
- 32. Запрет по В Множество А элементов, для которых высказывание А - истинно Множество В элементов, для
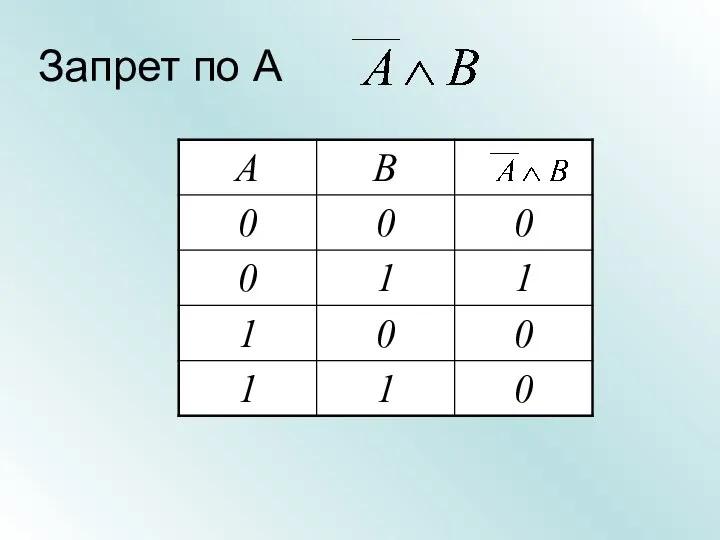
- 33. Запрет по А
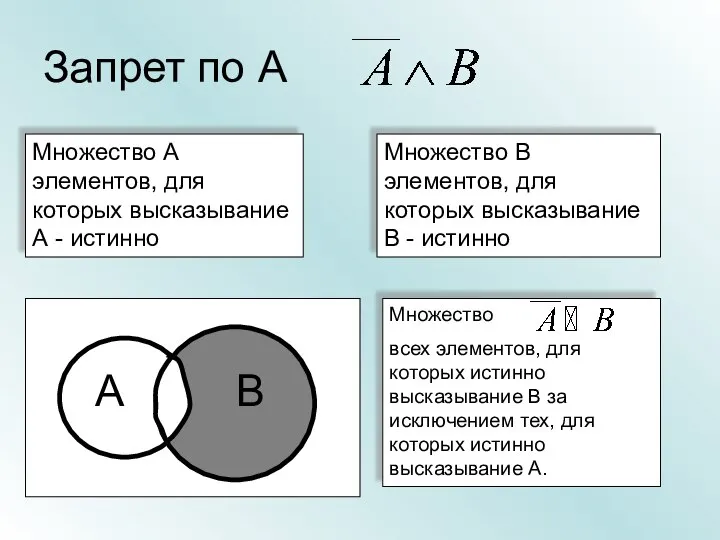
- 34. Запрет по А Множество А элементов, для которых высказывание А - истинно Множество В элементов, для
- 36. Элементарная конъюнкция Конъюнкция переменных функции или их отрицаний.
- 37. Дизъюнктивная нормальная форма (ДНФ) Дизъюнкция элементарных конъюнкций
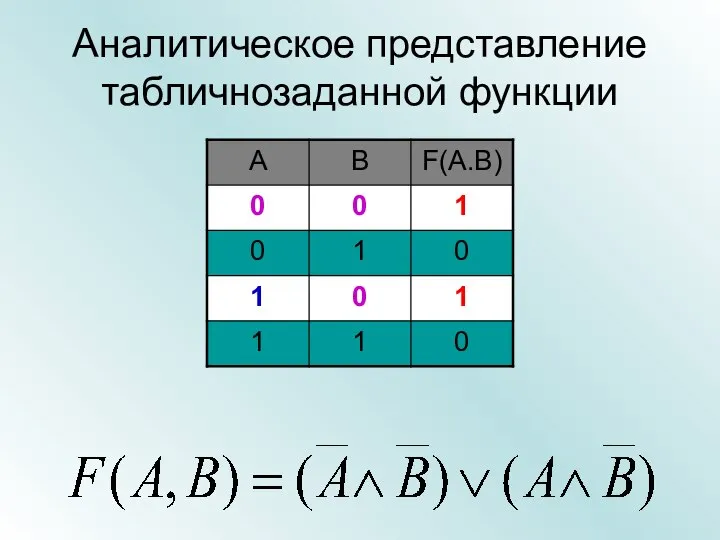
- 38. Аналитическое представление табличнозаданной функции
- 39. Элементарная дизъюнкция Дизъюнкция переменных функции или их отрицаний.
- 40. Конъюнктивная нормальная форма (КНФ) Конъюнкция элементарных дизъюнкций
- 41. Таким образом, отметим следующие определения:
- 44. Пример. По мишени производится стрельба 3-мя выстрелами и рассматриваются простые события: А1-попадание при 1-м выстреле, А2-попадание
- 46. Скачать презентацию

















 Путешествие в город Дробей на проспект Умножения. 6 класс
Путешествие в город Дробей на проспект Умножения. 6 класс Действительный анализ. Теорема Лебега (примеры). Измеримые множества
Действительный анализ. Теорема Лебега (примеры). Измеримые множества Как умножали египтяне
Как умножали египтяне Площадь многоугольника
Площадь многоугольника Решение систем неравенств с одной переменной
Решение систем неравенств с одной переменной Оценка математического ожидания и дисперсии отклика в отдельных точках факторного пространства
Оценка математического ожидания и дисперсии отклика в отдельных точках факторного пространства Полигон частот в математической статистике
Полигон частот в математической статистике Лінейныя ўраўненні з адной зменнай
Лінейныя ўраўненні з адной зменнай Расчёт скорости официанта от кассы до столика
Расчёт скорости официанта от кассы до столика Объём тела
Объём тела Теорема о плоскости, касательной к шару
Теорема о плоскости, касательной к шару Площадь круга и секторов
Площадь круга и секторов Куб
Куб Корень степени n
Корень степени n Построение биссектрисы угла. Билеты
Построение биссектрисы угла. Билеты Урок математики 20.09
Урок математики 20.09 Презентация на тему РЕШЕНИЕ ДРОБНЫХ РАЦИОНАЛЬНЫХ УРАВНЕНИЙ
Презентация на тему РЕШЕНИЕ ДРОБНЫХ РАЦИОНАЛЬНЫХ УРАВНЕНИЙ  Занимательные математические задания
Занимательные математические задания Сравнение групп предметов. Свойства предметов (1 класс)
Сравнение групп предметов. Свойства предметов (1 класс) Математическая модель колонны многокомпонентной ректификации. Лекция 9
Математическая модель колонны многокомпонентной ректификации. Лекция 9 Производная в заданиях уровня В. ЕГЭ
Производная в заданиях уровня В. ЕГЭ Неопределенный интеграл
Неопределенный интеграл Презентация на тему Простые числа
Презентация на тему Простые числа  История г. Колпашева в примерах и задачах
История г. Колпашева в примерах и задачах Сочетания. Свойства сочетаний. Бином Ньютона
Сочетания. Свойства сочетаний. Бином Ньютона Основные понятия теории вероятностей
Основные понятия теории вероятностей Возрастание и убывание функций. Экстремумы
Возрастание и убывание функций. Экстремумы Памятка по оформлению краткой записи к задачам (1 класс)
Памятка по оформлению краткой записи к задачам (1 класс)