Слайд 2Таблица производных и примеры нахождения производных функции одной переменной
Примеры нахождения производных

Слайд 3Нахождение частных производных – простые примеры
Пример 1. Найдите частные производные функции
Исследуемая функция

представляет собой сумму
5 других разных функций – распишем как производную суммы
В функции 2 переменных – х и у, значит, будет существовать 2 частных производных первого порядка
Возьмем производную по х, считая у и все функции чисто по у числами (а числа можно вынести за знак производной)
Кроме того, распишем все правила – в 5-м примере х и у есть и в числителе, и знаменателе, поэтому распишем по правилу производной от частного
Слайд 4Нахождение частных производных – простые примеры
Распишем производные от всех слагаемых
Следовательно,

Слайд 5Нахождение частных производных – простые примеры
Аналогично возьмем производные по у
Следовательно,

Слайд 6Нахождение частных производных – усложненные примеры
Пример 2. Найдите частные производные функции
Частные производные

от сложных функций берутся по тем же правилам, что и производные сложных функций, и частные производные; но необходимо помнить, что если функция является сложной только по одной переменной, то производная по другой переменной будет равна 0





 Задачи на движение в одном направлении из одной точки
Задачи на движение в одном направлении из одной точки Матрицы и действия над ними
Матрицы и действия над ними Разложение многочлена на множители
Разложение многочлена на множители Применение производной для исследования функции на монотонность и экстремумы
Применение производной для исследования функции на монотонность и экстремумы Тригонометрические уравнения и математические термины на английском языке
Тригонометрические уравнения и математические термины на английском языке Определители второго и третьего порядка
Определители второго и третьего порядка Решение систем уравнений с двумя переменными методом подстановки
Решение систем уравнений с двумя переменными методом подстановки Правильные многоугольники
Правильные многоугольники Основы анализа данных. Корреляционный анализ. (Лекция 5)
Основы анализа данных. Корреляционный анализ. (Лекция 5) Презентация на тему Число и цифра 7 (1 класс)
Презентация на тему Число и цифра 7 (1 класс)  Интерактивный тренажер. Числа от 1 до 1000. Нумерация (3 класс)
Интерактивный тренажер. Числа от 1 до 1000. Нумерация (3 класс) Презентация на тему Первый признак равенства треугольников
Презентация на тему Первый признак равенства треугольников  Время и работа. Связь между величинами
Время и работа. Связь между величинами Построение 3 видов группы геометрических тел
Построение 3 видов группы геометрических тел Решение простейших тригонометрических уравнений с помощью единичной окружности
Решение простейших тригонометрических уравнений с помощью единичной окружности Прямоугольный параллепипед. Итоговое повторение
Прямоугольный параллепипед. Итоговое повторение Признаки параллелограмма. 8 класс
Признаки параллелограмма. 8 класс Знакочередующиеся и знакопеременные ряды
Знакочередующиеся и знакопеременные ряды Величины. Объём
Величины. Объём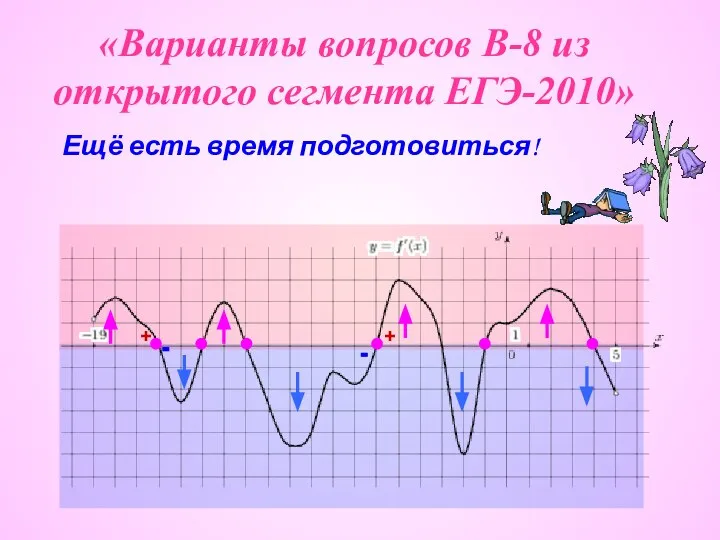 Варианты вопросов В-8 из открытого сегмента ЕГЭ-2010
Варианты вопросов В-8 из открытого сегмента ЕГЭ-2010 Задачи на кратное сравнение
Задачи на кратное сравнение Entrant
Entrant Решение задач (1 класс)
Решение задач (1 класс) Касательная плоскость к сфере
Касательная плоскость к сфере Наука Метрология
Наука Метрология Задача з піцою
Задача з піцою Тригонометрические уравнения
Тригонометрические уравнения Вычисление логарифмов
Вычисление логарифмов