Геометрические определения

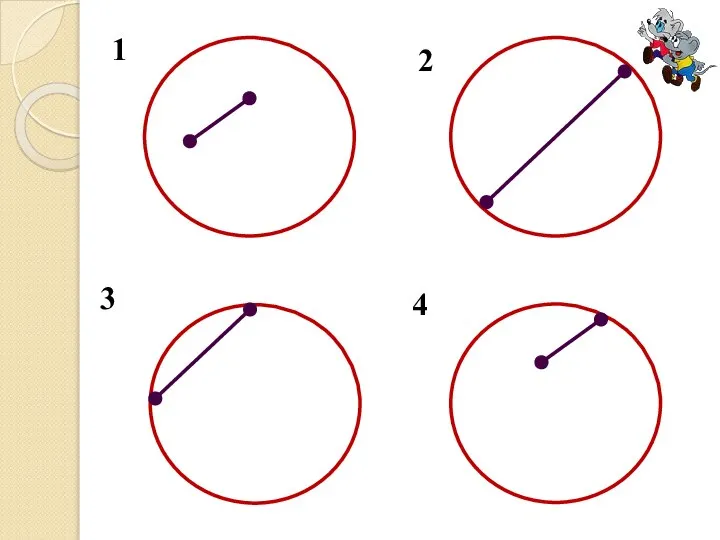
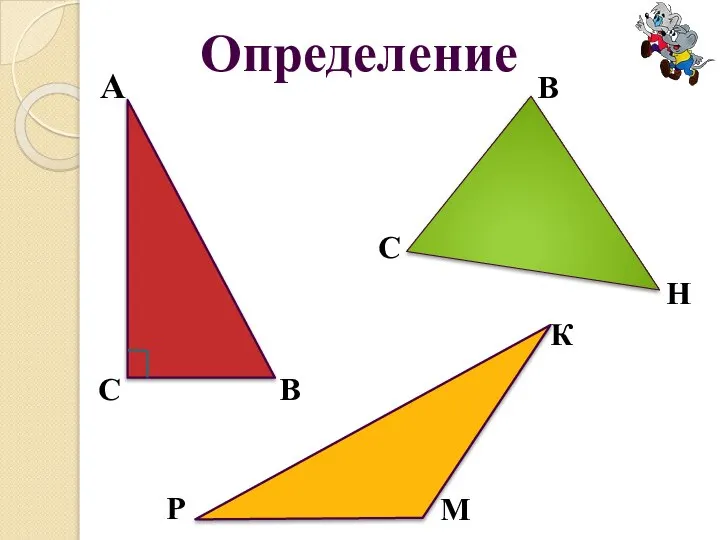
Определение
Отрезок, соединяющий две точки окружности, называется хордой окружности.

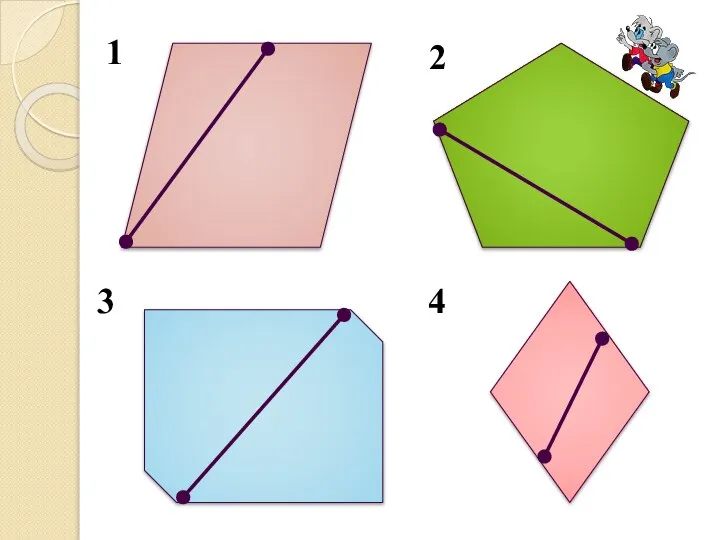
Определение
Диагональю многоугольника называется отрезок, соединяющий любые две его несоседние вершины.

3

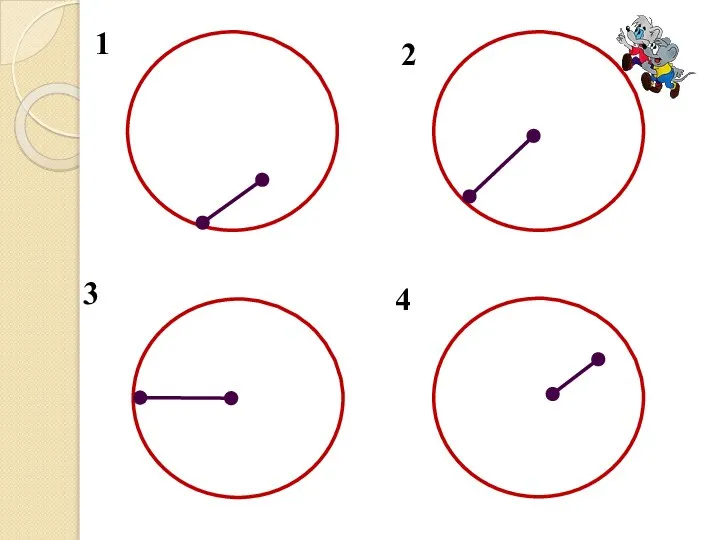
Определение
Отрезок, соединяющий центр окружности с какой-либо её точкой, называется радиусом окружности.

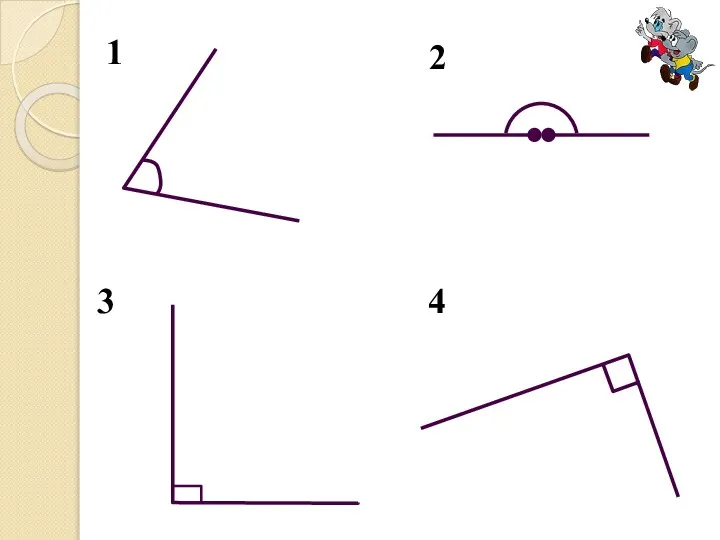
Определение
Угол, градусная мера которого равна 90 градусов, называется прямым.

Определение
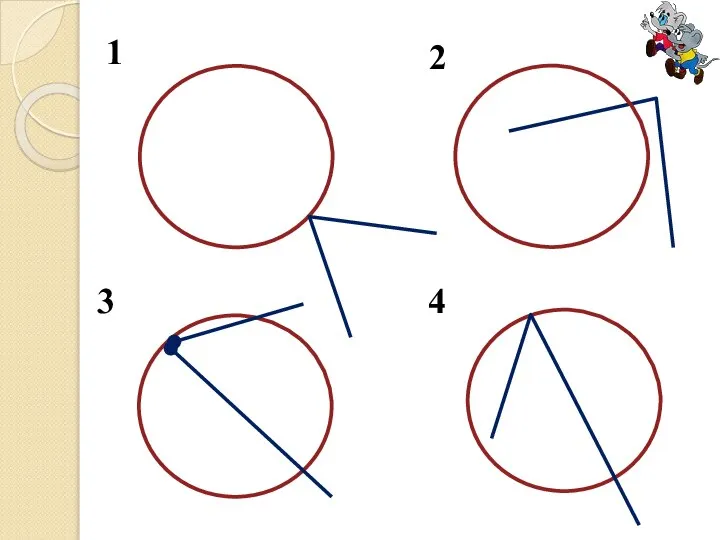
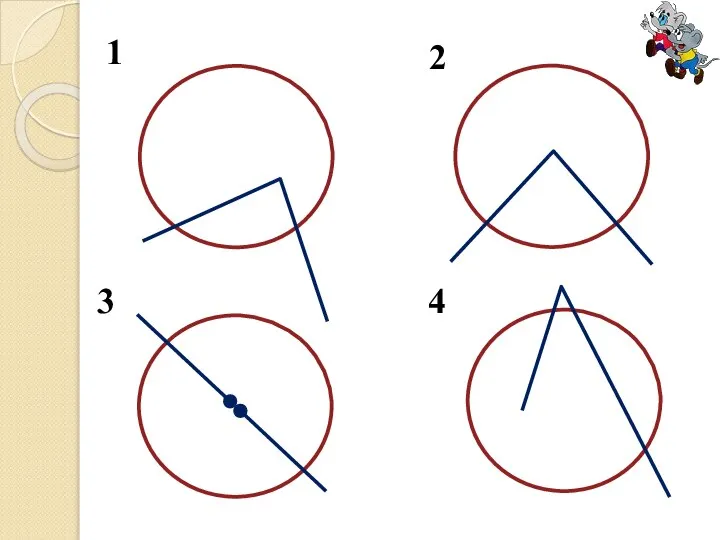
Угол, вершина которого лежит на окружности, а стороны пересекают эту окружность, называется вписанным углом.

1
3

Определение
Угол с вершиной в центре окружности называется её центральным углом.

Определение
А

Определение
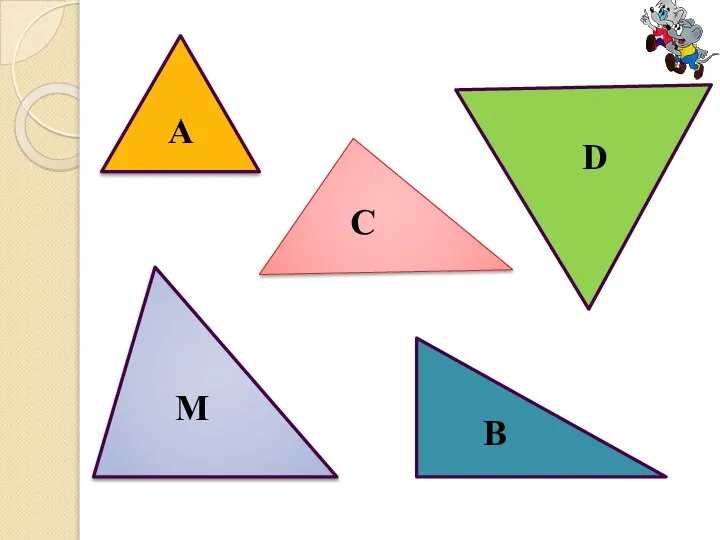
Треугольник называется равносторонним, если все его стороны имеют одинаковую длину.

A
B
C
M
D

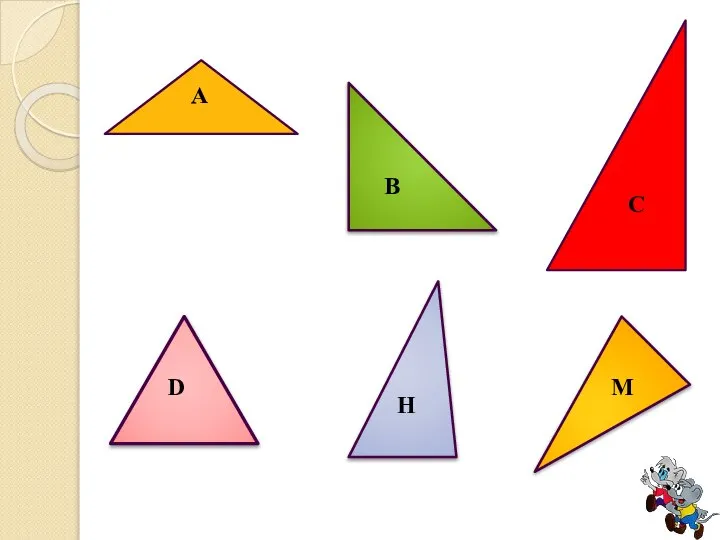
Выберите на рисунке равносторонний треугольник. Назовите треугольник.
Измерьте углы этого треугольника.
Запишите чему они равны.
Сформулируйте гипотезу.
Определение

В равностороннем треугольнике соедините отрезками середины сторон.
Что вы замечаете?
Сформулируйте гипотезу.
Определение

Определение
Треугольник называется равнобедренным, если хотя бы две из его стороны имеют одинаковую длину.

A
B
C
D
H
M

Является ли равнобедренный треугольник равносторонним?
Является ли равносторонний треугольник равнобедренным?
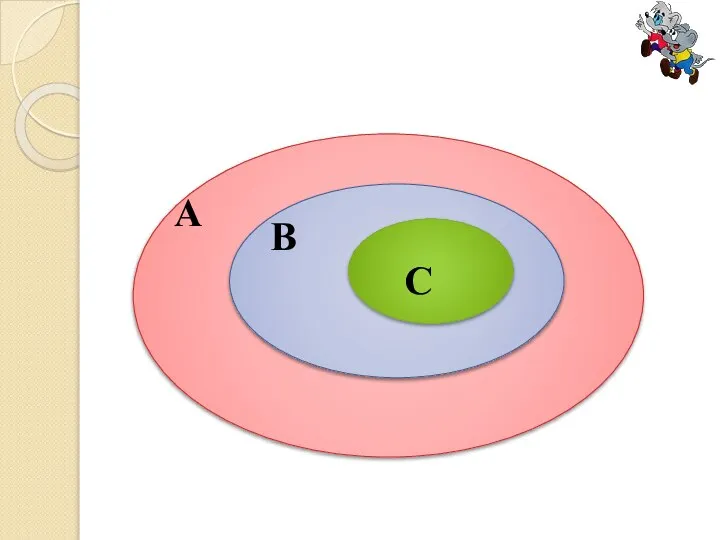
А – множество всех треугольников;
В – множество равнобедренных
треугольников;
С – множество равносторонних
треугольников.
Постройте диаграмму Эйлера-Венна
для множеств А, В и С.

А
В
С