Содержание
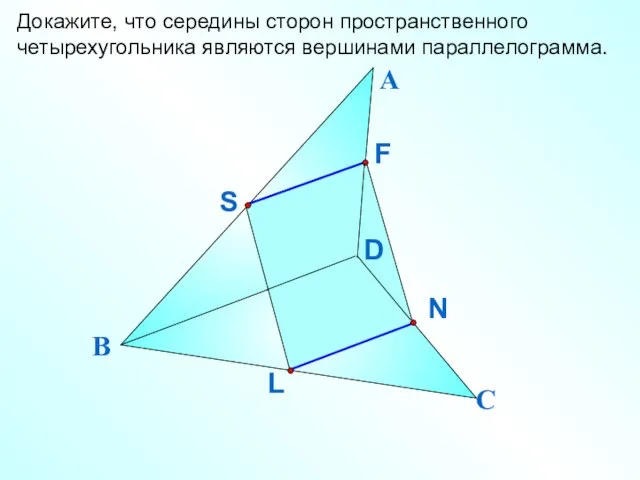
- 2. Докажите, что середины сторон пространственного четырехугольника являются вершинами параллелограмма. А В С D
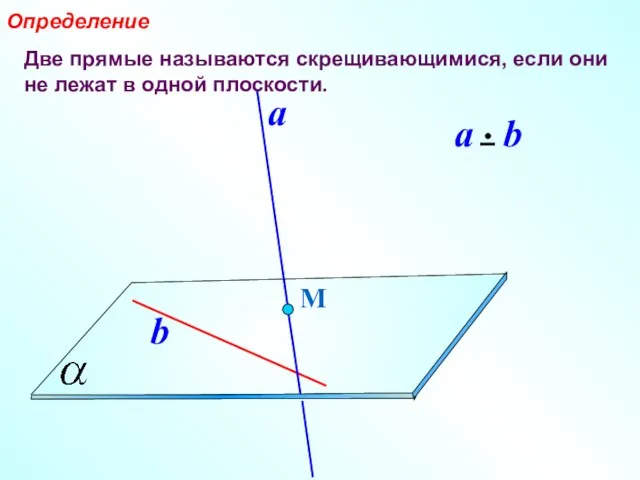
- 3. Две прямые называются скрещивающимися, если они не лежат в одной плоскости. Определение М a b
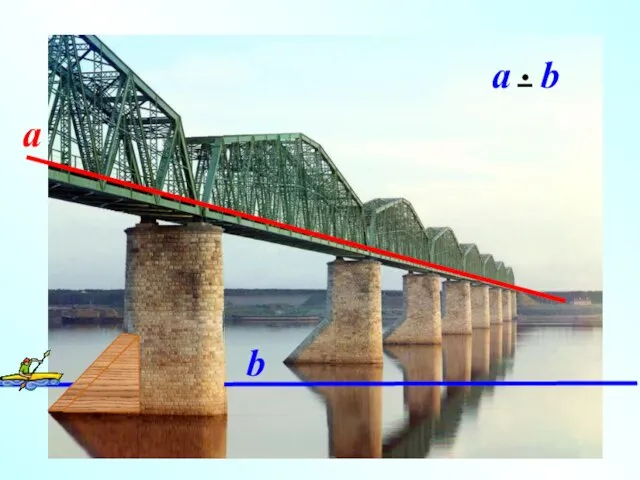
- 4. IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIi Наглядное представление о скрещивающихся прямых дают две дороги, одна из которых проходит по эстакаде, а
- 5. a b
- 6. Найдите на рисунке параллельные прямые. Назовите параллельные прямые и плоскости. Найдите скрещивающиеся прямые.
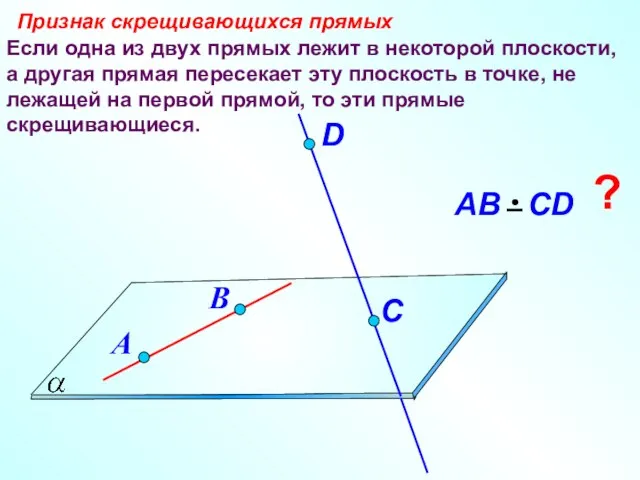
- 7. Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в
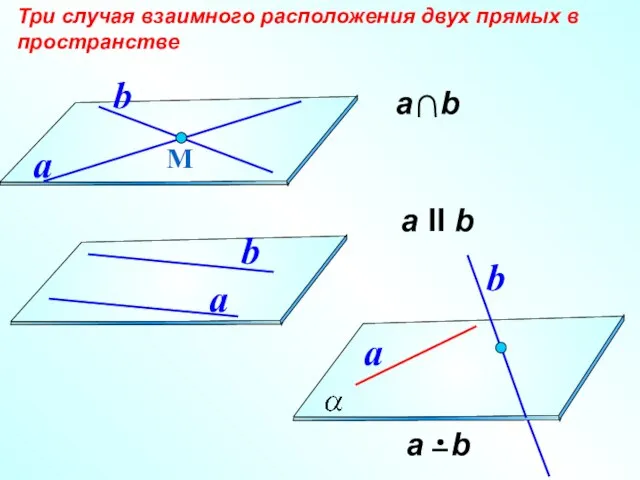
- 8. а II b Три случая взаимного расположения двух прямых в пространстве М a b a b
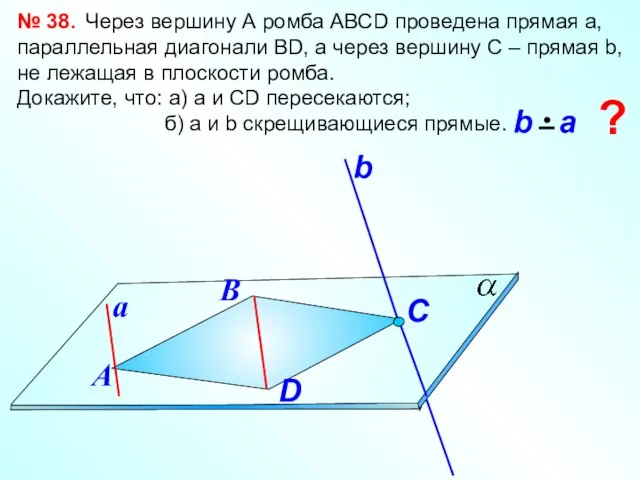
- 9. № 38. Через вершину А ромба АВСD проведена прямая а, параллельная диагонали ВD, а через вершину
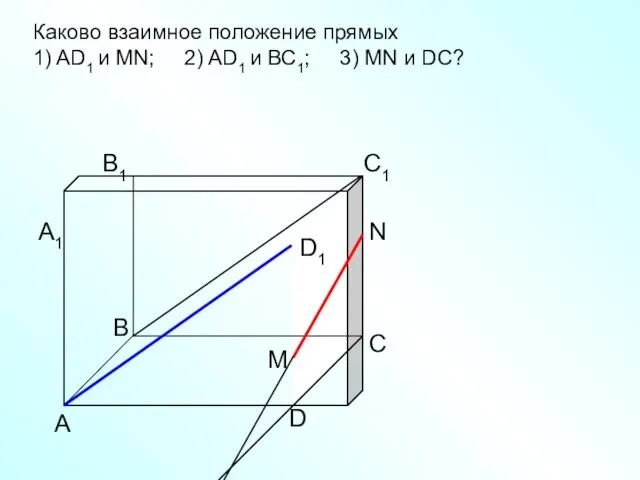
- 10. А D С В B1 С1 D1 А1 Каково взаимное положение прямых 1) AD1 и МN;
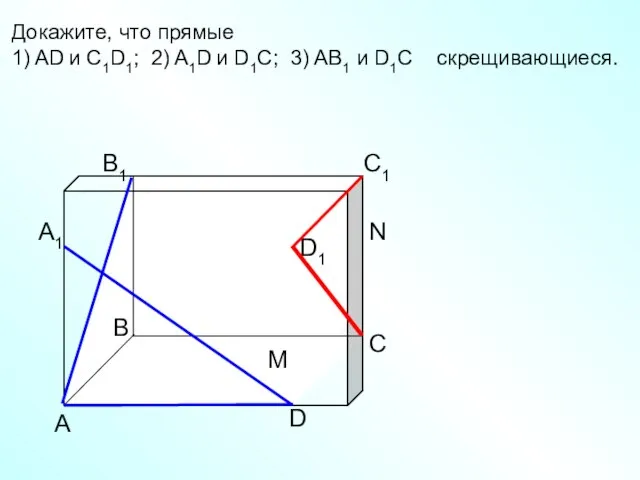
- 11. А D С В B1 С1 D1 А1 Докажите, что прямые 1) AD и C1D1; 2)
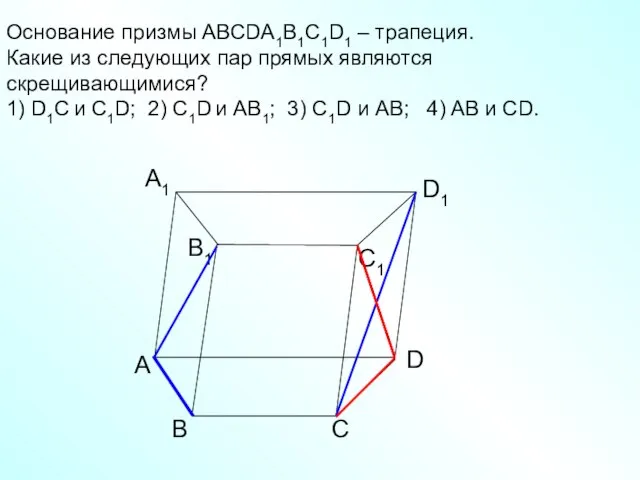
- 12. А D С В B1 С1 D1 А1 Основание призмы АВСDA1B1C1D1 – трапеция. Какие из следующих
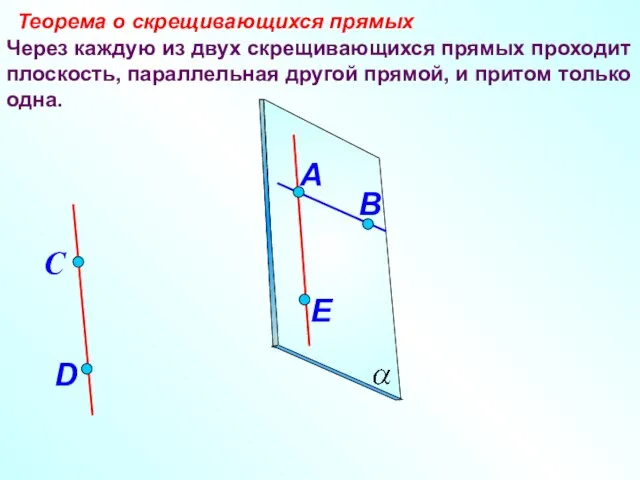
- 13. Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой прямой, и притом только одна. Теорема
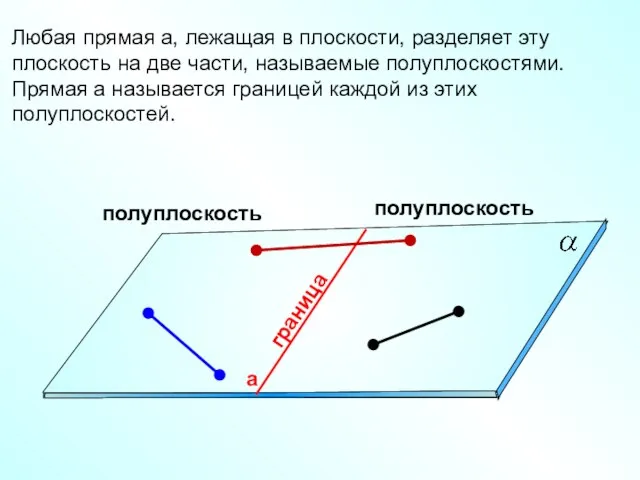
- 14. полуплоскость полуплоскость граница Любая прямая а, лежащая в плоскости, разделяет эту плоскость на две части, называемые
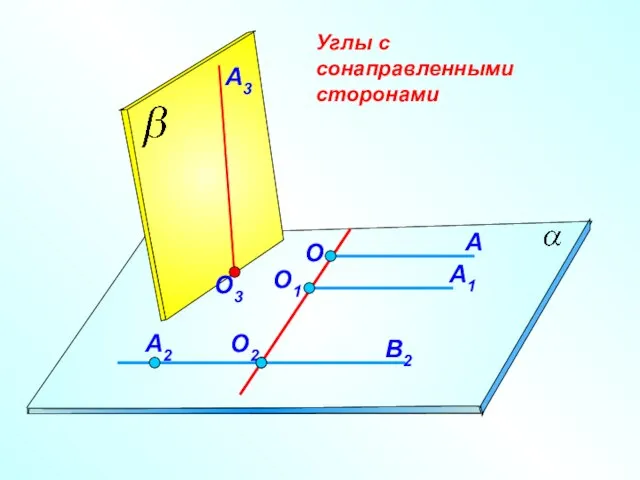
- 15. Углы с сонаправленными сторонами A О О1 О2 A1 В2 A2 О3 A3
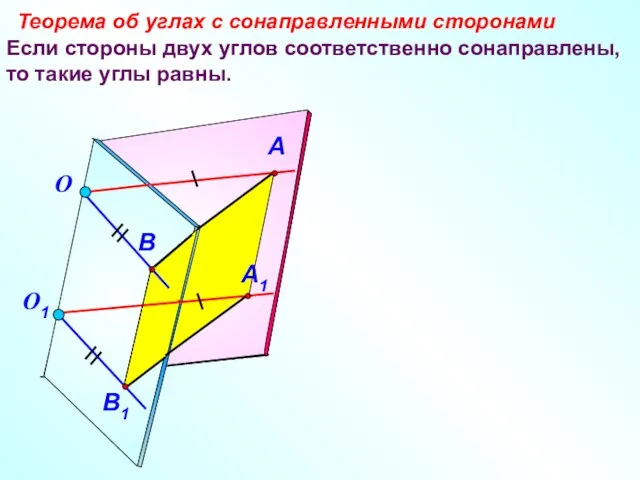
- 16. Если стороны двух углов соответственно сонаправлены, то такие углы равны. Теорема об углах с сонаправленными сторонами
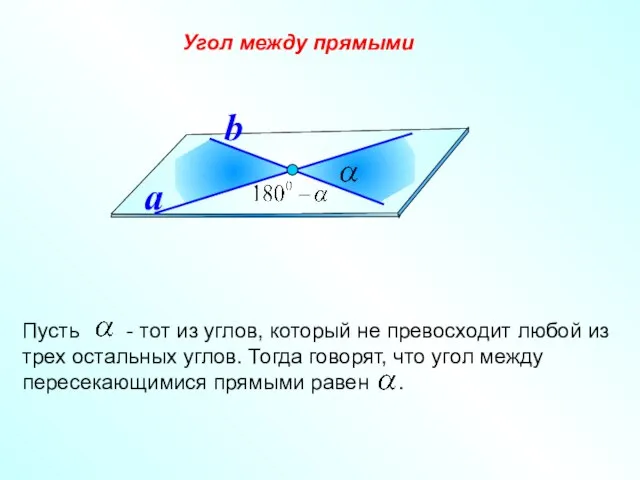
- 17. Угол между прямыми a b
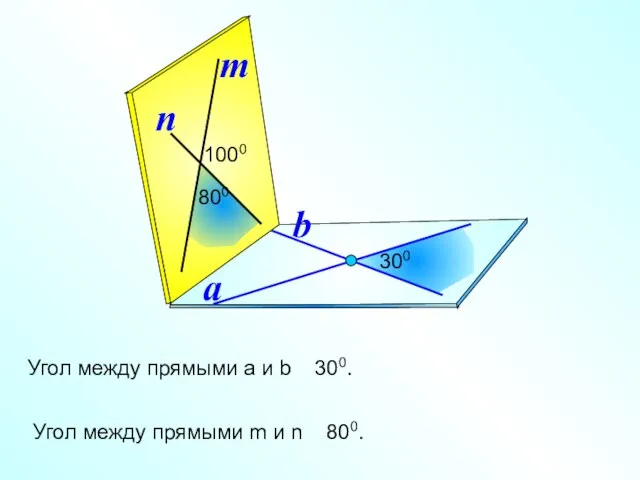
- 18. a b 300 n 1000 m Угол между прямыми m и n 800. Угол между прямыми
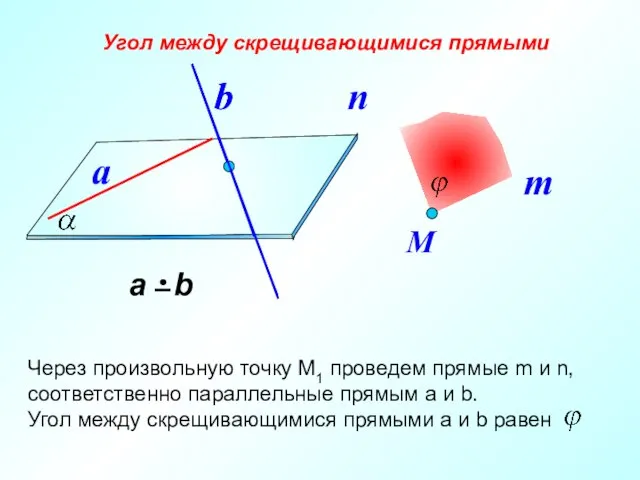
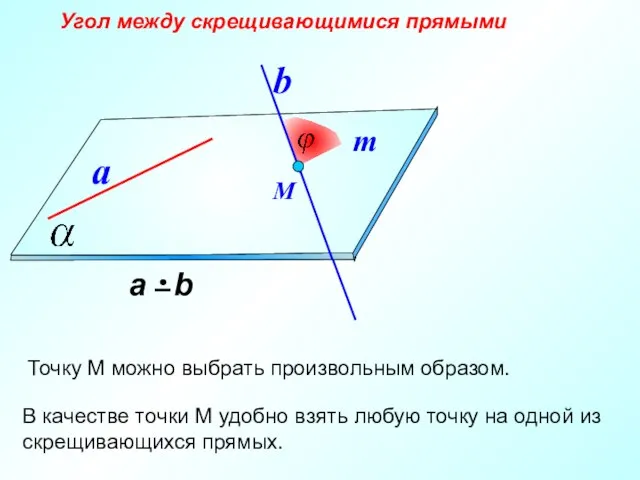
- 19. Угол между скрещивающимися прямыми a b b М
- 20. Угол между скрещивающимися прямыми a b М Точку М можно выбрать произвольным образом. m В качестве
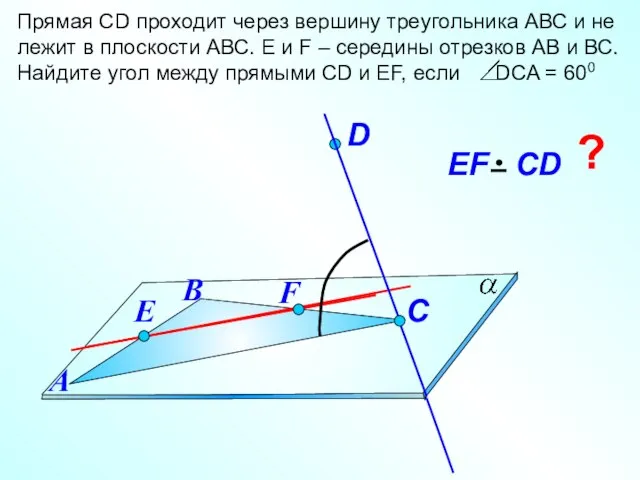
- 21. Прямая СD проходит через вершину треугольника АВС и не лежит в плоскости АВС. E и F
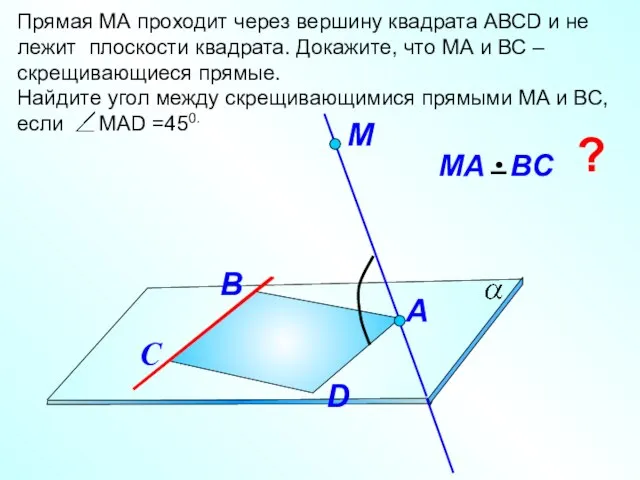
- 22. Прямая МА проходит через вершину квадрата АВСD и не лежит плоскости квадрата. Докажите, что МА и
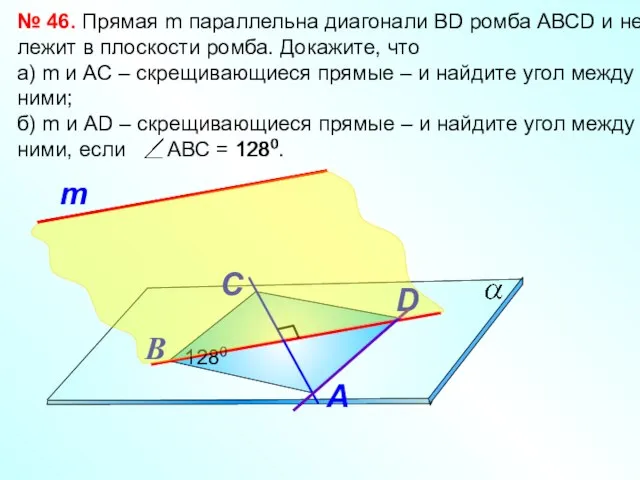
- 23. № 46. Прямая m параллельна диагонали ВD ромба АВСD и не лежит в плоскости ромба. Докажите,
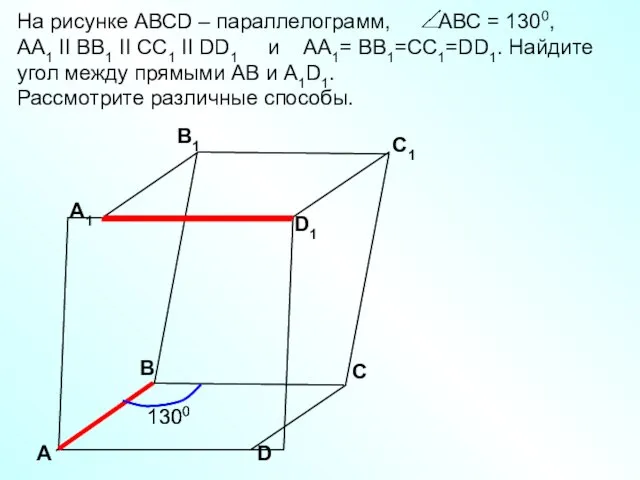
- 24. А D С А1 B1 С1 D1 В На рисунке АВСD – параллелограмм, АВС = 1300,
- 26. Скачать презентацию


 Вписанная окружность
Вписанная окружность Брейн-ринг
Брейн-ринг Презентация на тему Использование здоровьесберегающих технологий на уроках математики
Презентация на тему Использование здоровьесберегающих технологий на уроках математики  МатШах(0.1)
МатШах(0.1)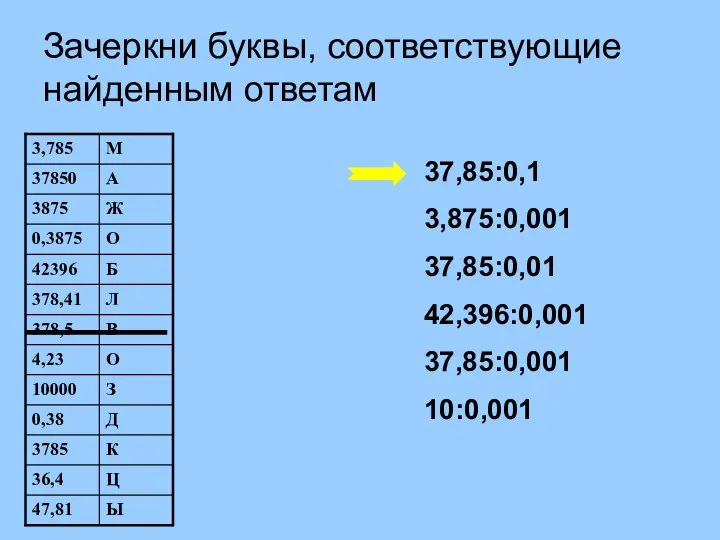 Устная работа (1). Зачеркни буквы, соответствующие найденным ответам
Устная работа (1). Зачеркни буквы, соответствующие найденным ответам Логарифмические уравнения и неравенства. Практическая работа
Логарифмические уравнения и неравенства. Практическая работа Повторение по математике
Повторение по математике Понятие вектора
Понятие вектора Занимательные задачи
Занимательные задачи Вычислить. Задание на лето
Вычислить. Задание на лето Оформление заданий по математике согласно федеральным образовательным стандартам Программа школа 2100
Оформление заданий по математике согласно федеральным образовательным стандартам Программа школа 2100 Свойство углов при основании равнобедренного треугольника
Свойство углов при основании равнобедренного треугольника Прямоугольный треугольник
Прямоугольный треугольник Звёздчатые многогранники
Звёздчатые многогранники Вычисление площади фигур на клетчатой бумаге
Вычисление площади фигур на клетчатой бумаге Вариационный ряд. Группировка данных при качественной и количественной вариациях
Вариационный ряд. Группировка данных при качественной и количественной вариациях Призма. Площадь поверхности призмы. 10 класс
Призма. Площадь поверхности призмы. 10 класс Расстояния в пространстве
Расстояния в пространстве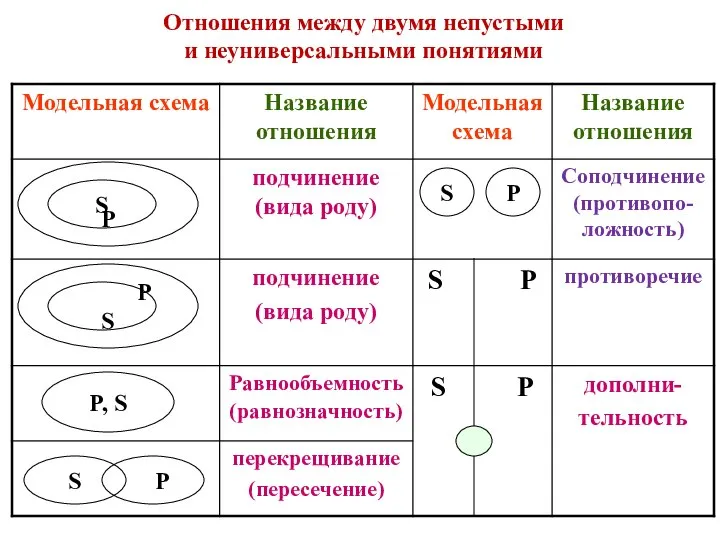 Отношения между двумя непустыми и неуниверсальными понятиями. Модельная схема
Отношения между двумя непустыми и неуниверсальными понятиями. Модельная схема Презентация на тему График функции (7 класс)
Презентация на тему График функции (7 класс)  В мире многогранников
В мире многогранников Нормальная интерполяция
Нормальная интерполяция Графики функций. Задачи с параметрами
Графики функций. Задачи с параметрами Стереометрия. Аксиомы стереометрии
Стереометрия. Аксиомы стереометрии Решение системы линейных уравнений. Методы решения системы линейных уравнений
Решение системы линейных уравнений. Методы решения системы линейных уравнений Метрическая система мер
Метрическая система мер Перпендикулярность плоскостей
Перпендикулярность плоскостей Уравнения и неравенства с одной переменной
Уравнения и неравенства с одной переменной