Содержание
- 2. 09/01/2023 Ребята! Сегодня мы с вами выходим в открытое пространство. Объект изучения – скрещивающиеся прямые. Вы
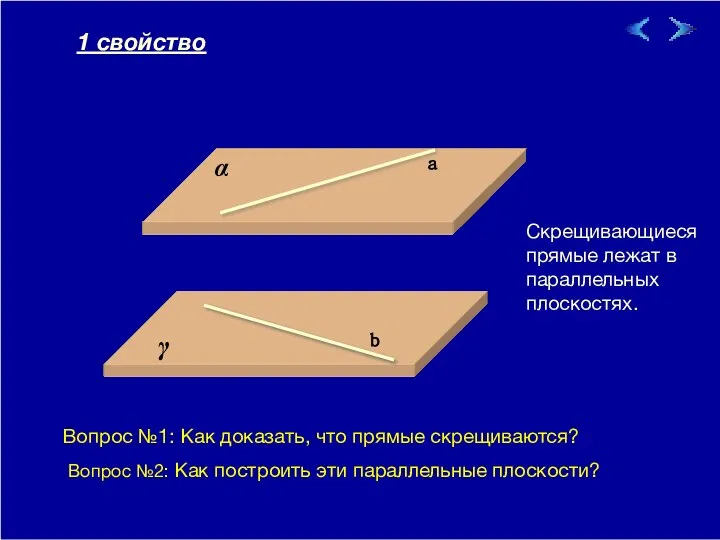
- 3. 09/01/2023 Скрещивающиеся прямые лежат в параллельных плоскостях. α γ b a 1 свойство Вопрос №1: Как
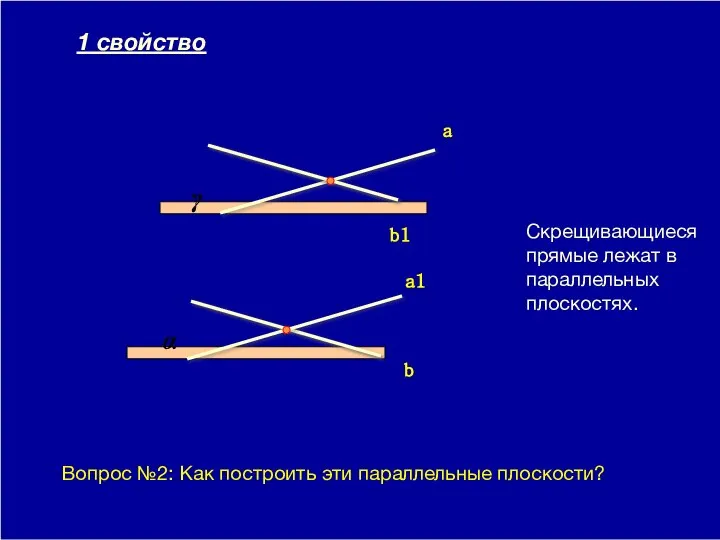
- 4. 09/01/2023 Скрещивающиеся прямые лежат в параллельных плоскостях. α γ b a 1 свойство Вопрос №2: Как
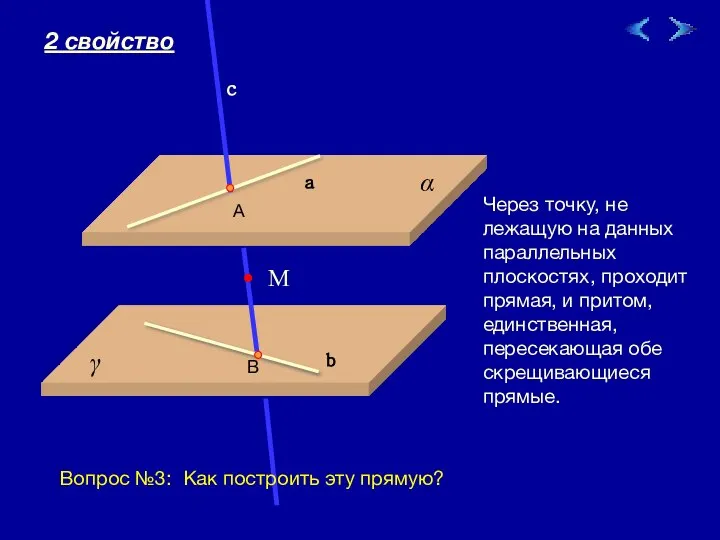
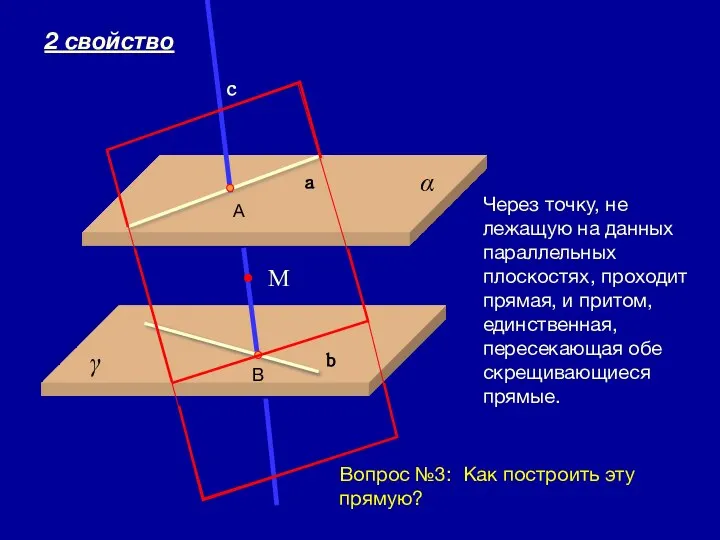
- 5. 09/01/2023 Через точку, не лежащую на данных параллельных плоскостях, проходит прямая, и притом, единственная, пересекающая обе
- 6. 09/01/2023 Через точку, не лежащую на данных параллельных плоскостях, проходит прямая, и притом, единственная, пересекающая обе
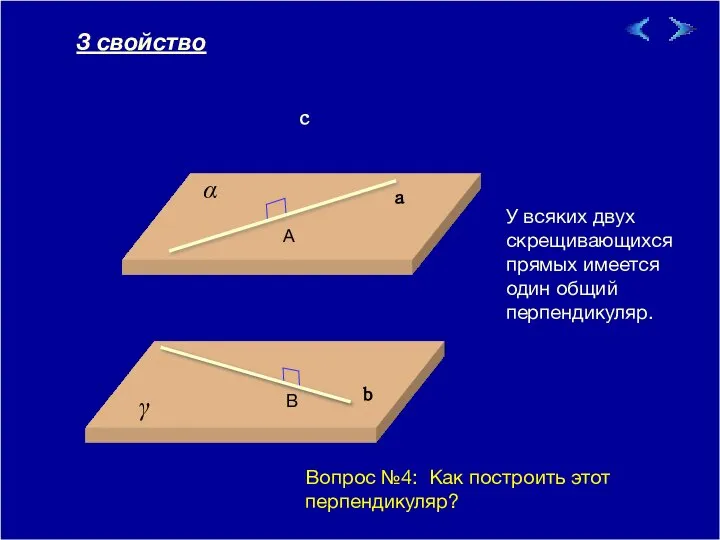
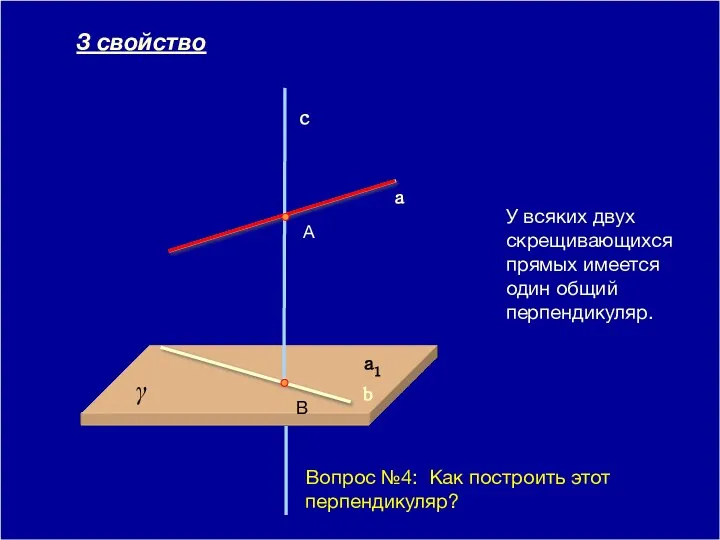
- 7. 09/01/2023 У всяких двух скрещивающихся прямых имеется один общий перпендикуляр. γ α a b c A
- 8. 09/01/2023 У всяких двух скрещивающихся прямых имеется один общий перпендикуляр. γ a b c A B
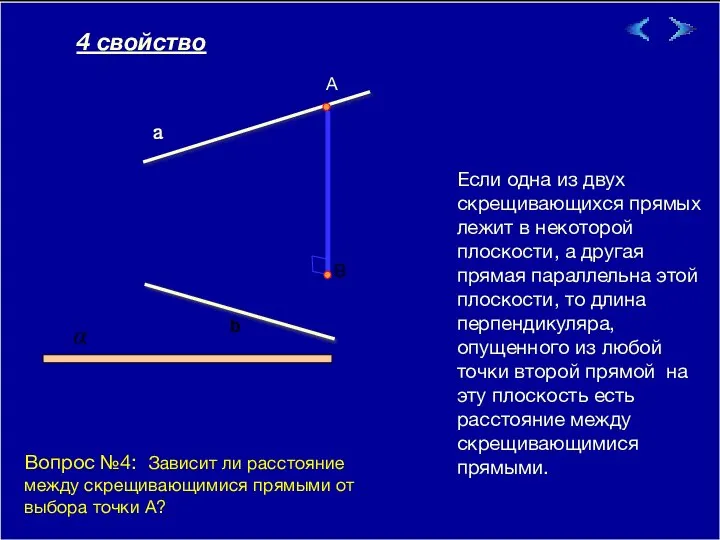
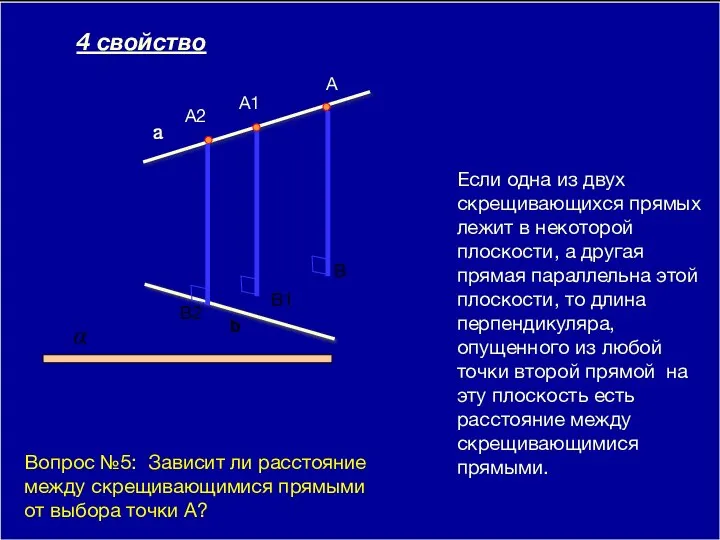
- 9. 09/01/2023 Если одна из двух скрещивающихся прямых лежит в некоторой плоскости, а другая прямая параллельна этой
- 10. 09/01/2023 Если одна из двух скрещивающихся прямых лежит в некоторой плоскости, а другая прямая параллельна этой
- 11. 09/01/2023 Теперь вы догадываетесь, какие интересные конструкции можно составлять из скрещивающихся прямых. Без скрещивающихся ребер нет
- 12. 09/01/2023 Вы видите пары скрещивающихся ребер.
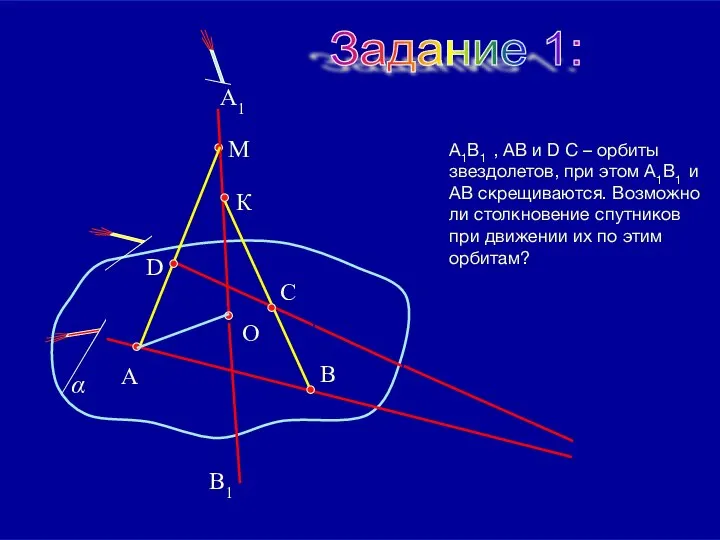
- 13. 09/01/2023 А1В1 , АВ и D С – орбиты звездолетов, при этом А1В1 и АВ скрещиваются.
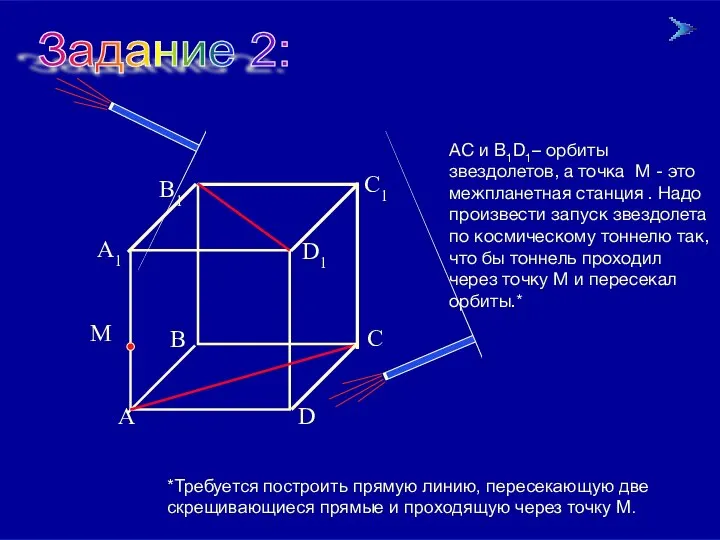
- 14. 09/01/2023 АС и В1D1– орбиты звездолетов, а точка М - это межпланетная станция . Надо произвести
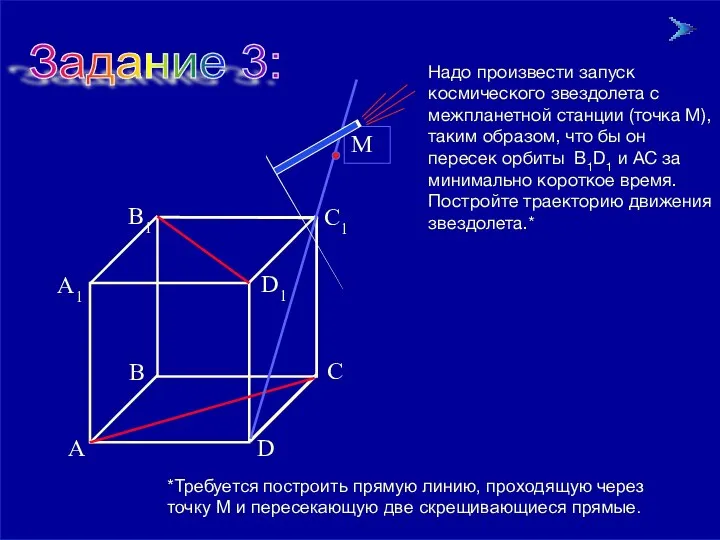
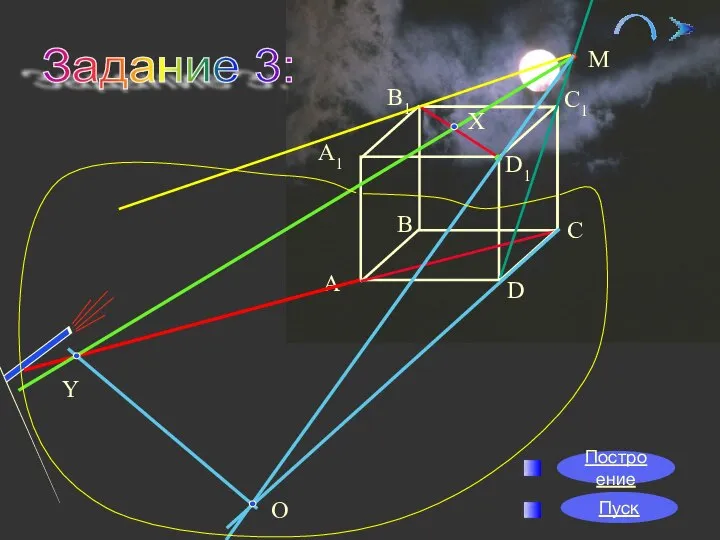
- 15. 09/01/2023 Задание 3: B1 Надо произвести запуск космического звездолета с межпланетной станции (точка М), таким образом,
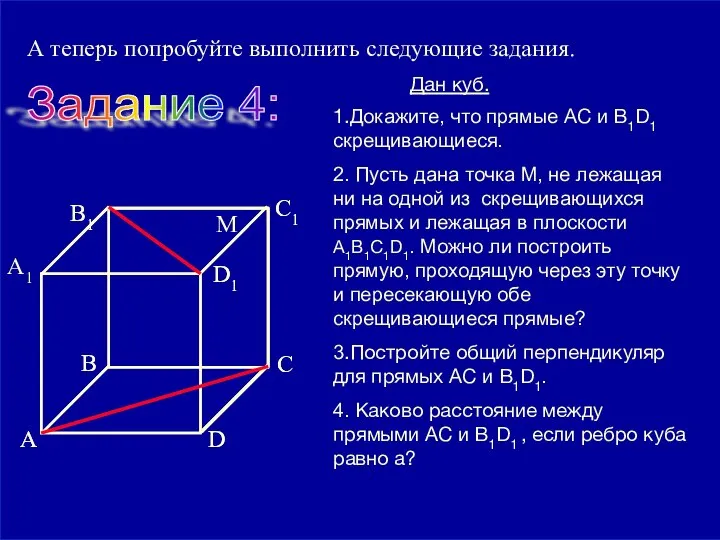
- 16. 09/01/2023 А теперь попробуйте выполнить следующие задания. Задание 4: 1.Докажите, что прямые АС и B1D1 скрещивающиеся.
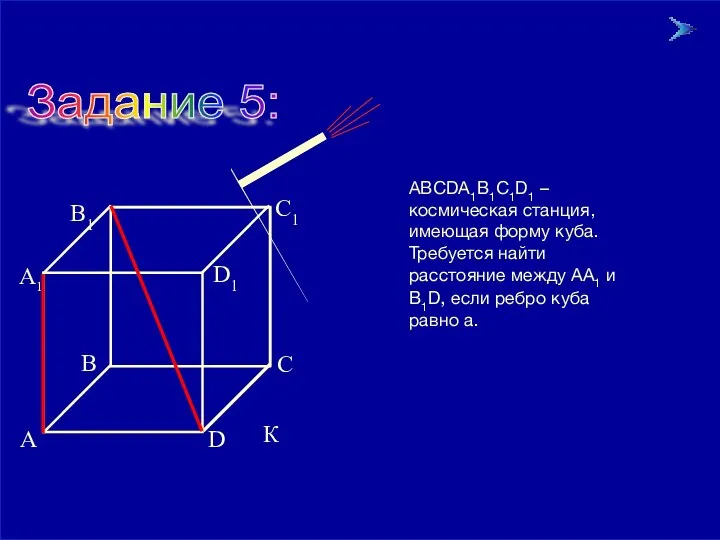
- 17. 09/01/2023 Задание 5: АВСDА1В1С1D1 – космическая станция, имеющая форму куба. Требуется найти расстояние между АА1 и
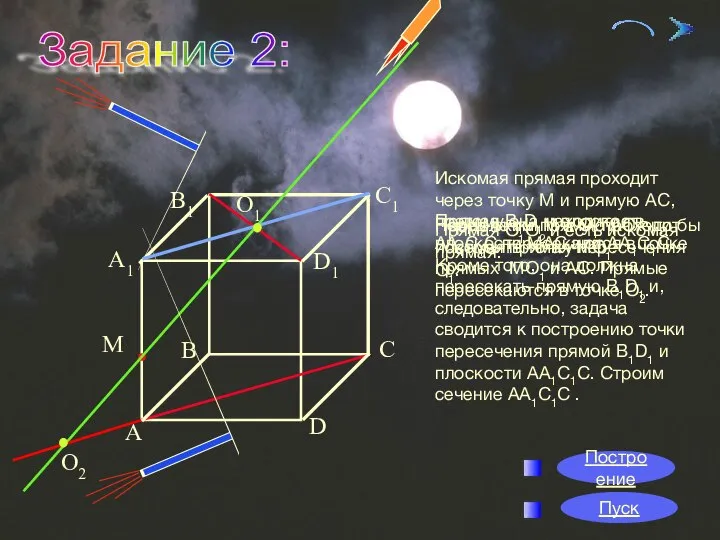
- 18. 09/01/2023 О1 О2 Задание 2: Искомая прямая проходит через точку М и прямую АС, поэтому она
- 19. 09/01/2023 Задание 3: C1 А B C D D1 A1 В1 М Y X Построение Пуск
- 20. 09/01/2023 Задание 5: О Построение Замечаем, что прямая В1D лежит в плоскости сечения ВВ1D1D, а прямая
- 21. 09/01/2023 Ответы: Т.к. прямые лежат в параллельных плоскостях, то они не пересекаются, а т.к. они не
- 23. Скачать презентацию





 Показательная функция
Показательная функция Векторы в пространстве. Понятие вектора
Векторы в пространстве. Понятие вектора Сотая часть
Сотая часть Направления геймификации современного образовательного процесса на уроках математики и информатики и во внеурочной деятельности
Направления геймификации современного образовательного процесса на уроках математики и информатики и во внеурочной деятельности Корреляционный анализ. (Тема 3)
Корреляционный анализ. (Тема 3) Понятие процента
Понятие процента Линейные функции
Линейные функции Особенности итогового повторения
Особенности итогового повторения Основы геометрии (5 класс)
Основы геометрии (5 класс) Презентация на тему "Взаимно обратные числа" 6 класс
Презентация на тему "Взаимно обратные числа" 6 класс  Многогранники, 10 класс
Многогранники, 10 класс Десятичные дроби
Десятичные дроби Применение теории графов
Применение теории графов Тригонометрические формулы
Тригонометрические формулы Площадь параллелограмма
Площадь параллелограмма Окружность и круг. Повторение 7 класс
Окружность и круг. Повторение 7 класс первые уроки геометрии
первые уроки геометрии Равенство фигур
Равенство фигур Конкурс капитанов
Конкурс капитанов Свойства показательной функции
Свойства показательной функции Применение графов
Применение графов Процентное содержание компонентов
Процентное содержание компонентов Презентация на тему Деление двузначного числа на однозначное
Презентация на тему Деление двузначного числа на однозначное  А-11 Триг функции и их свойства 29.09.22 - копия
А-11 Триг функции и их свойства 29.09.22 - копия Тригонометрические уравнения
Тригонометрические уравнения Габриэль Крамер
Габриэль Крамер Сумма углов треугольника. Решение задач
Сумма углов треугольника. Решение задач Графический диктант. Тема: Делимость чисел
Графический диктант. Тема: Делимость чисел