Содержание
- 2. Определение. Углом между прямыми называется меньший из двух углов между лучами, которые этим прямым соответственно параллельны.
- 3. Перпендикулярными будут называться любые две прямые, угол между которыми 90°, Определение. Прямая называется перпендикулярной плоскости, если
- 4. Верно ли, что прямая, перпендикулярная двум сторонам треугольника, перпендикулярна его третьей стороне?
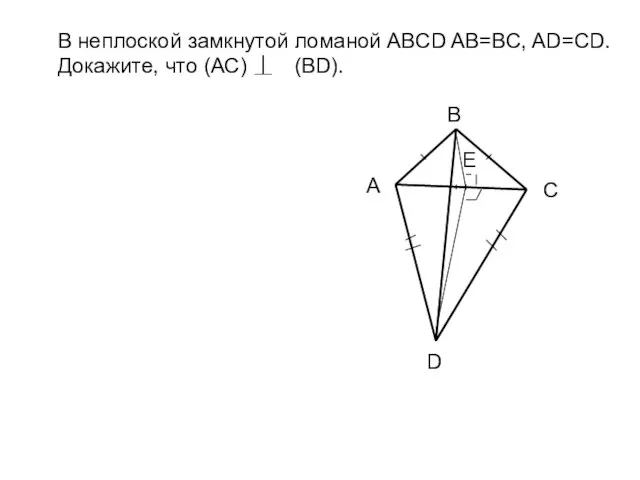
- 5. В неплоской замкнутой ломаной ABCD AB=BC, AD=CD. Докажите, что (АС) (BD). В А Е С D
- 6. Точка А не лежит на прямой а. Какую фигуру образуют все прямые, проходящие через точку А
- 7. Проверьте равносильность утверждений: Две прямые перпендикулярны Через каждую из них проходит плоскость, перпендикулярная другой прямой 2)
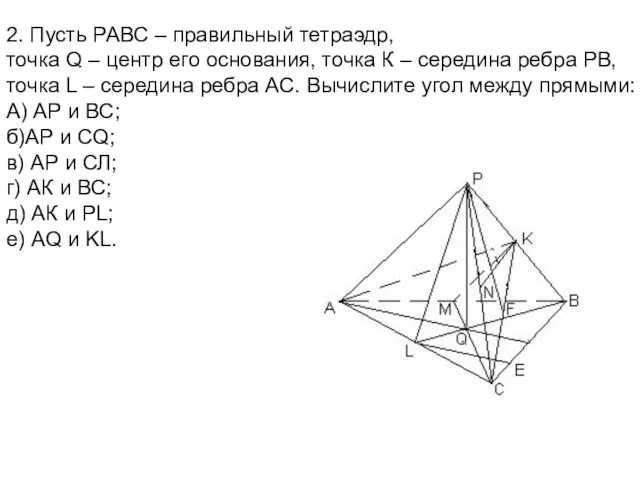
- 8. 2. Пусть РАВС – правильный тетраэдр, точка Q – центр его основания, точка К – середина
- 10. Скачать презентацию





 Случаи вычитания 11 -
Случаи вычитания 11 - Статистические графики
Статистические графики математика гр 32 парність-2.docx
математика гр 32 парність-2.docx Число та цифра 6
Число та цифра 6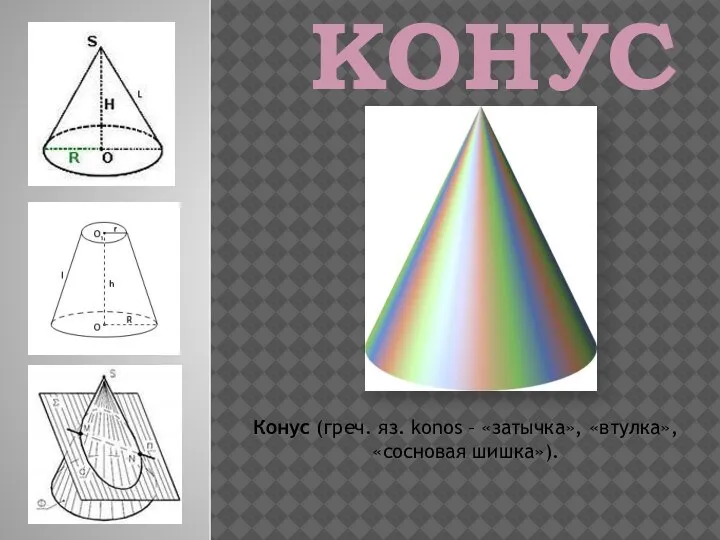 Конус. Виды конусов. Конусы в нашей жизни
Конус. Виды конусов. Конусы в нашей жизни Сечения в многогранниках
Сечения в многогранниках Уравнение линии на плоскости. Уравнение фигуры. Уравнение окружности
Уравнение линии на плоскости. Уравнение фигуры. Уравнение окружности Решение задач с помощью уравнений
Решение задач с помощью уравнений Решение задач на движение
Решение задач на движение Понятие спирали
Понятие спирали Геометрические построения
Геометрические построения Элементы теории вероятностей
Элементы теории вероятностей Проценты
Проценты Математические ребусы
Математические ребусы Площади. ОГЭ
Площади. ОГЭ Средняя линия треугольника (8 класс)
Средняя линия треугольника (8 класс) Текстовые задачи на движение по прямой
Текстовые задачи на движение по прямой Основное свойство дроби
Основное свойство дроби Две задачи на дроби
Две задачи на дроби Статистические гипотезы
Статистические гипотезы Собираем ягоды. Математика 1 класс. Итоговое повторение. Тренажёр
Собираем ягоды. Математика 1 класс. Итоговое повторение. Тренажёр Конструктивные объекты
Конструктивные объекты Математика: психология и нейронауки. Чем нейробиология и когнитивная психология могут помочь учителю математики?
Математика: психология и нейронауки. Чем нейробиология и когнитивная психология могут помочь учителю математики? Презентация по математике "Что такое понятие" -
Презентация по математике "Что такое понятие" -  Параллельность плоскостей
Параллельность плоскостей Экономический биатлон. “Экономика и математика”. Финал
Экономический биатлон. “Экономика и математика”. Финал Методичні основи ознайомлення здобувачів освіти з діями множення і ділення, зв'язком між ними
Методичні основи ознайомлення здобувачів освіти з діями множення і ділення, зв'язком між ними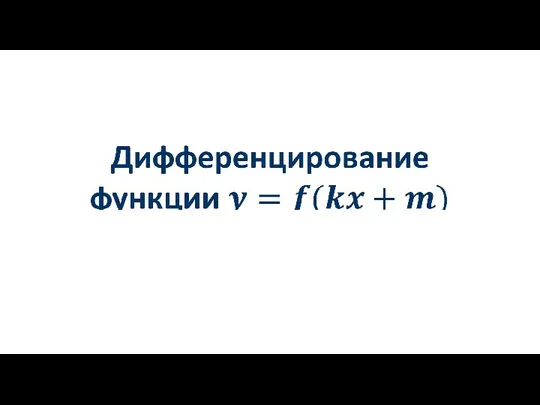 Дифференцирование функции y=f(kx+m)
Дифференцирование функции y=f(kx+m)