3_TEMA_3_Matematicheskaya_logika_1

1. Операции над высказываниями.
Определение. Под высказыванием мы будем понимать любое предложение, о котором можно судить истинно оно или ложно.
Примеры высказываний:
1. «Луна спутник Земли»,
2. «Волга впадает в Каспийское море»,
3. «Косинус 60 градусов равен 0,5»,
4. «Париж столица Англии»,
5. «Угол, вписанный в окружность равен дуге, на которую он опирается»
Пример 1. Какие из приведенных ниже предложений являются
высказываниями? Какие из этих высказываний истинны, а какие ложны?
1. Енисей является притоком Волги.
2. Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
3. Четырехугольник можно вписать в окружность тогда и только тогда, когда суммы его противоположных углов равны 180 градусов.
4. Диагонали параллелограмма всегда являются биссектрисами его углов.
5. Существуют внеземные цивилизации.

В примере 1 все 5 предложений являются высказываниями.
2-ое и 3-тье предложения – истинные высказывания,
1-ое и 4-ое предложения – ложные высказывания.
Предложения «Пейте пепси-колу», «Жуйте орбит без сахара» высказываниями не являются.
Высказывания мы будем обозначать маленькими буквами латинского алфавита: a, b, c, p, q, s и т.д.
Из высказываний, при помощи частицы «не», союзов «и», «или», слов «если-то», «тогда и только тогда, когда» могут образовываться новые высказывания.
Простейшей операцией над высказываниями является операция отрицания, которой соответствует частица «не».
Отрицание высказывания р обозначается . Если высказывание р истинно,
то -ложно.

Определение. Высказывание, составленное из данных высказываний p и q при помощи союза «и» называется конъюнкцией высказываний p и q.
Обозначается
Конъюнкция истинна только в случае, если оба высказывания p и q истинны.
Определение. Высказывание, составленное из данных высказываний p и q при помощи союза «или» называется дизъюнкцией высказываний p и q.
Обозначается
Дизъюнкция истинна , если хотя бы одно из двух высказываний p или q истинно.
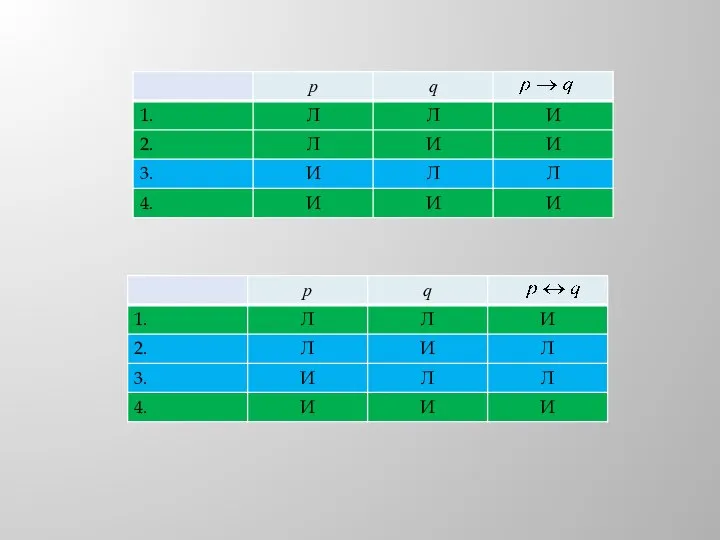
Определение. Высказывание, составленное из данных высказываний p и q при помощи слов «если…то» называется импликацией высказываний p и q. Обозначается При этом высказывание p называется условием, а q – заключением.
Импликация принимает значение ложно только если условие р- истинно, а заключение q- ложно. Из истинны не может следовать ложь. Если условие р – ложно, то импликация всегда принимает значение истинна, так как из лжи может следовать все, что угодно.

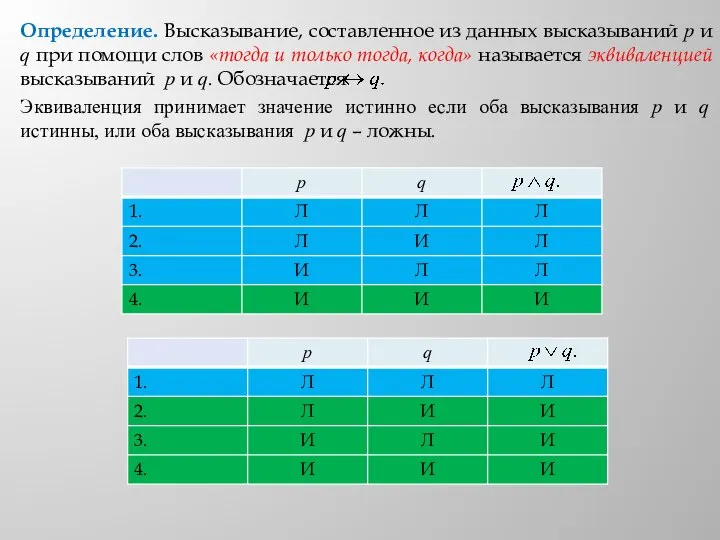
Определение. Высказывание, составленное из данных высказываний p и q при помощи слов «тогда и только тогда, когда» называется эквиваленцией высказываний p и q. Обозначается
Эквиваленция принимает значение истинно если оба высказывания p и q истинны, или оба высказывания p и q – ложны.

Пример 2. Составить таблицу истинности для высказывания
1.
2.
3.
4.

Пример 3. Составить таблицу истинности для высказывания
1.
2.
3.
4.
s- тождественно истинное высказывание.

Вместо И (истинна) мы будем писать 1, вместо Л (ложь) будем писать 0.
Законы логики высказываний.
Законы де Моргана.

Докажем закон поглощения Введем в рассмотрение высказывание
. Нам нужно доказать, что в таблице истинности для данного высказывания столбик s совпадает со столбиком р.
1.
2.
3.
4.
Столбец s совпадает со столбцом р