Методы решения логарифмических уравнений. 11 класс

Цель урока:
1. Систематизировать и обобщить знания учащихся по теме « Методы решения логарифмических уравнений»
2. Закрепить навыки решения логарифмических уравнений
3. Выполнить контролирующую самостоятельную работу

Логарифмические уравнения
Функционально-графический метод
log2x = -x + 1
Алгоритм решения:
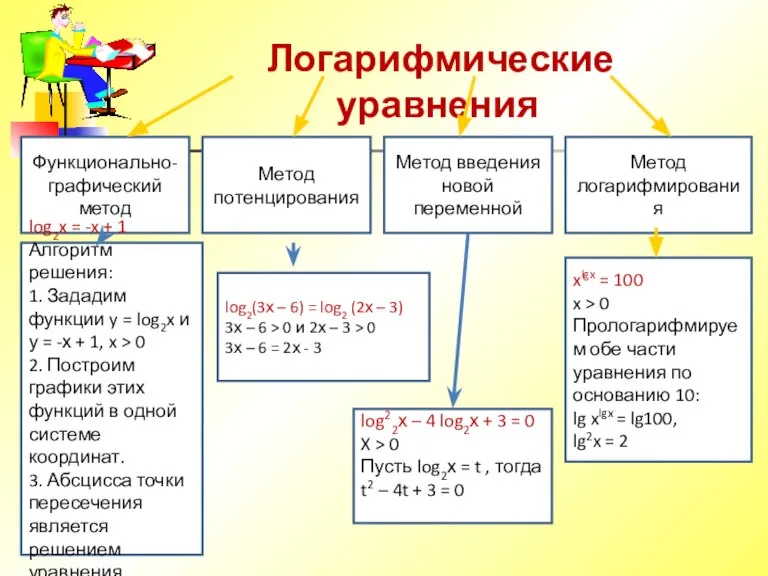
1. Зададим функции y = log2x и у = -х + 1, x > 0
2. Построим графики этих функций в одной системе координат.
3. Абсцисса точки пересечения является решением уравнения.
Метод потенцирования
log2(3х – 6) = log2 (2х – 3)
3х – 6 > 0 и 2х – 3 > 0
3х – 6 = 2х - 3
Метод введения новой переменной
log22х – 4 log2х + 3 = 0
X > 0
Пусть log2х = t , тогда t2 – 4t + 3 = 0
Метод логарифмирования
xlgx = 100
x > 0
Прологарифмируем обе части уравнения по основанию 10:
lg xlgx = lg100,
lg2x = 2