Случайные величины и их распределения

§3.1. Случайные величины
Случайной величиной называется величина (Х), которая в результате опыта может принимать одно из значений х1, х2,…, хi,…, хn, образующих полную группу несовместных событий, причем неизвестно заранее, какое именно.
Х= хi; Р(Х= хi)= рi
Дискретной (не непрерывной) случайной величиной называют случайную величину Х, которая принимает отдельные, изолированные возможные значения хi с определенными вероятностями рi.

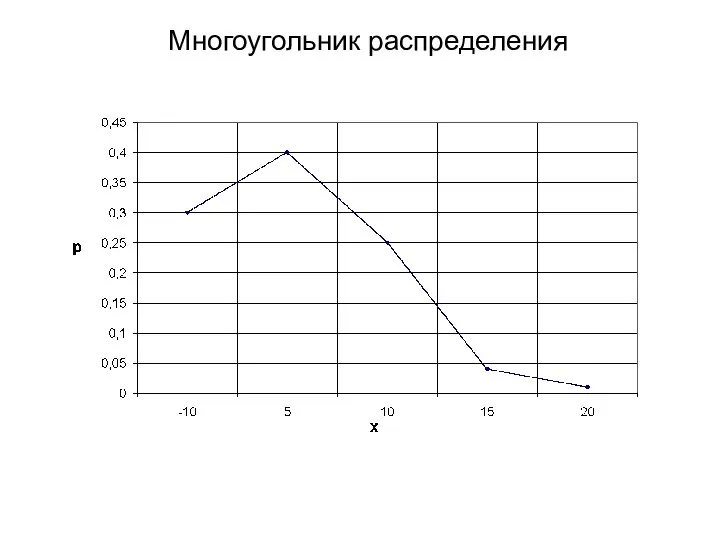
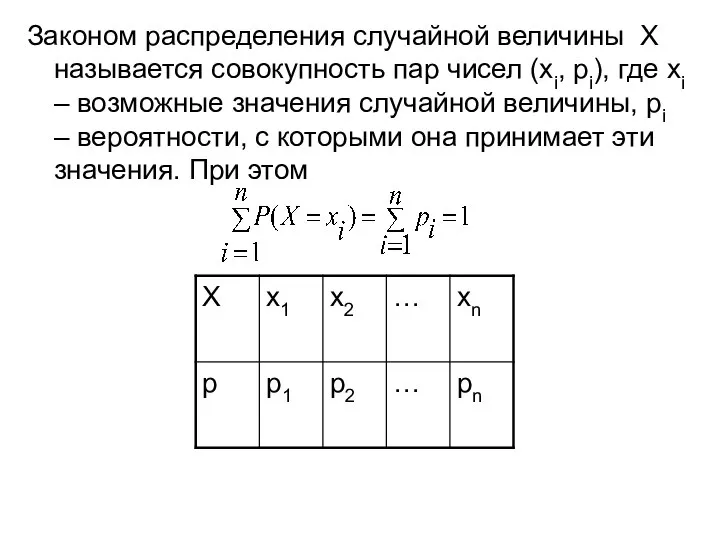
Законом распределения случайной величины Х называется совокупность пар чисел (хi, рi), где хi – возможные значения случайной величины, рi – вероятности, с которыми она принимает эти значения. При этом

Пример:

Многоугольник распределения

Непрерывной называют случайную величину, которая может принимать все значения из некоторого конечного или бесконечного промежутка. Число возможных значений случайной непрерывной величины бесконечно.
Числовая функция Х(ω) называется случайной величиной, если для любого ее возможного значения хi ∈ Ω = (-∞<хi<∞), где множество Ω есть множество элементарных событий ω, определена вероятность Р{X(ω)

§3.2. Числовые характеристики случайной внличины
В теории вероятностей числовые характеристики условно можно разделить на две группы:
– характеристики положения;
– характеристики рассеивания и вероятностных взаимодействий.

§3.2.1. Характеристики положения
Математическое ожидание, мода и медиана.
N независимых испытаний; СВ принимает определенные значения х1, х2,…, хi,…, хn.
Причем, х1 благоприятствовали m1 случаев, х2 - m2 случаев, далее хn - mn случаев.
Арифметическое значений СВ Х обозначим через М[X]:
М[X]=
где

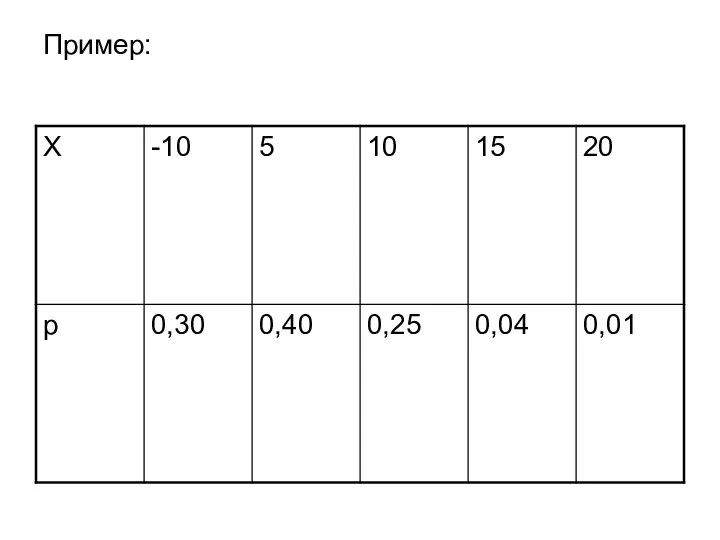
Если ряд сходится абсолютно и
, то М[X]=
Для дискретной СВ М[X]=
Для непрерывной СВ М[X]=
Свойства МО СВ:
1. М[C]=C;
2. M[CX]=CM[X];
3. M[X1+X2+… +Xn]= M[X1]+M[X2]+…+ M[Xn];
4. M[X1X2… Xn]= M[X1]M[X2]… M[Xn].

Кроме МО вводят такие характеристики, как мода (Мо) и медиана (Ме).
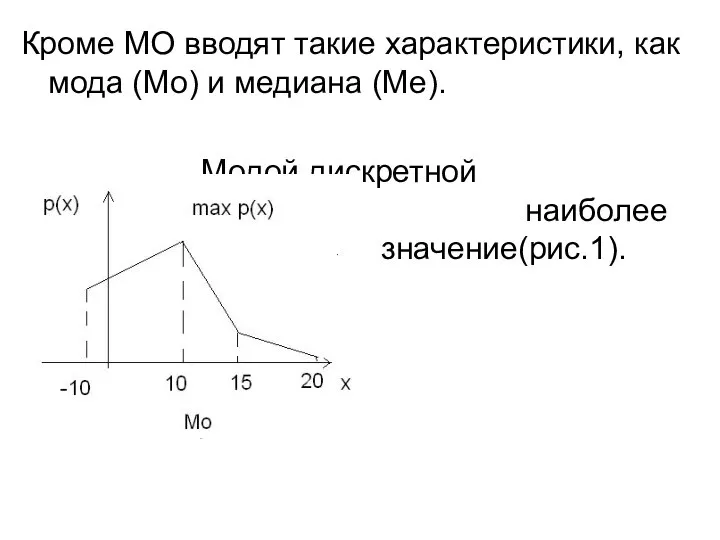
Модой дискретной СВ называется ее наиболее вероятное значение(рис.1).
Рис.1

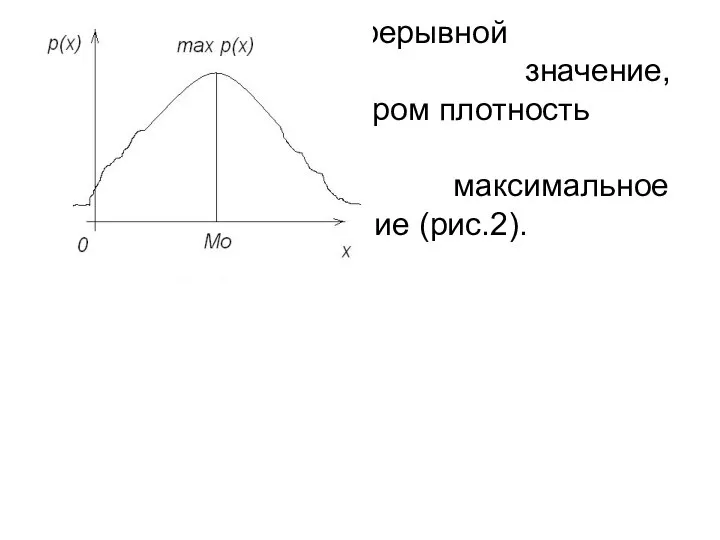
Модой непрерывной СВ называется ее значение, при котором плотность вероятности принимает максимальное Рис.2 значение (рис.2).

Медианой СВ называется такое ее значение Ме, для которого P(X
=P(X>Me)=0,5
(рис.3).
Рис.3
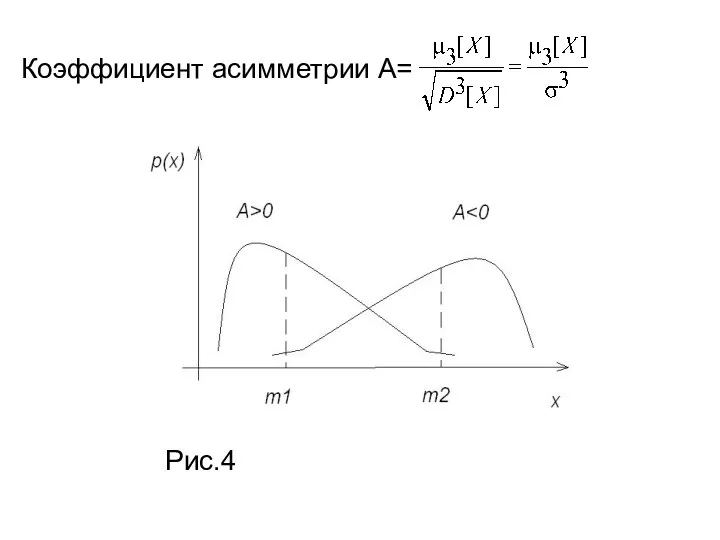
Симметричное распределение: M[X]=Mo=Me

§3.2.2. Характеристики рассеивания и взаимодействия
Моменты двух видов: начальные и центральные.
Начальным моментом k-го порядка αk[X] СВ Х называется МО k-ой степени от этой СВ, т.е. αk[X]=M[Xk].
Для дискретной СВ: αk[X]=
Для непрерывной СВ: αk[X]=

Центрированной СВ Х°, соответствующей СВ Х, называется отклонение СВ от ее МО M[X]=m, т.е. Х°=Х-m.
M[X°]=0.
Для дискретной СВ Х: M[X°]=M[X-m]=
=
Центральным моментом k-го порядка μk[X] СВ Х называется МО k-ой степени центрированной СВ X°, т.е. μk[X]= M[(X°)k]=M[(X-m)k].

Для дискретной СВ Х: μk[X]=
Для непрерывной СВ Х: μk[X]=
=
μ1[X]=M[X°]= M[X-m]=0.
μ2[X]= M[(X°)2]=M[(X-m)2]= =
=

μ2[X]=D[X]=Dx=σ2 .
Для дискретной СВ:D[X]= M[(X°)2]= M[(X-
-m)2]=
Для непрерывной СВ: D[X]=
=
Среднее квадратическое или стандартное отклонение СВ σ: σ=

Свойства дисперсии:
D[X]≥0. При Х=С : D[С]=0.
D[СX]=С2D[X].
D[X1+X2+… +Xn]= D[X1] + D[Х2] + …+ D[Хn].
D[С+Х]= D[Х].
D[Х-Y]= D[Х]+D[Y].
D[Х+Y]= D[Х]+D[Y]+2K(x,y).

Коэффициент асимметрии А=
Рис.4