Содержание
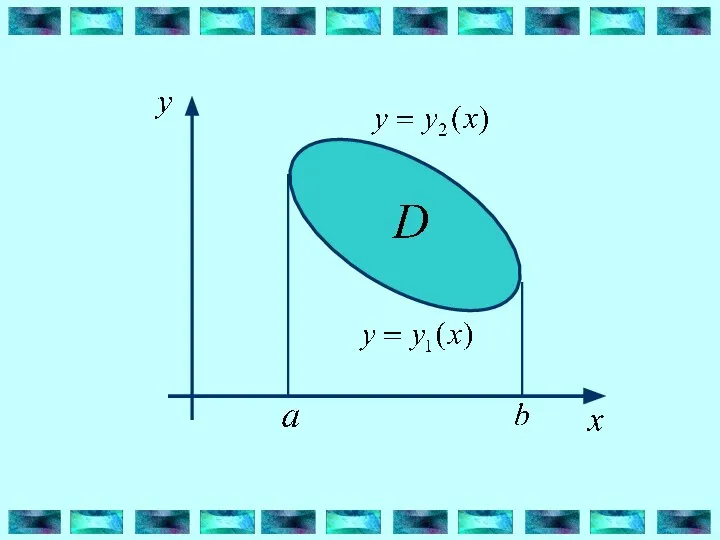
- 2. ТЕОРЕМА. Пусть функция z=f(x,y) определена и интегрируема в области D, ограниченную снизу и сверху двумя непрерывными
- 3. Тогда существует повторный интеграл и выполняется равенство:
- 6. Если D –прямоугольная область, т.е. тогда
- 7. ПРИМЕРЫ. 1 Вычислить двойной интеграл
- 8. РЕШЕНИЕ.
- 9. 2 Вычислить двойной интеграл где область D ограничена линиями
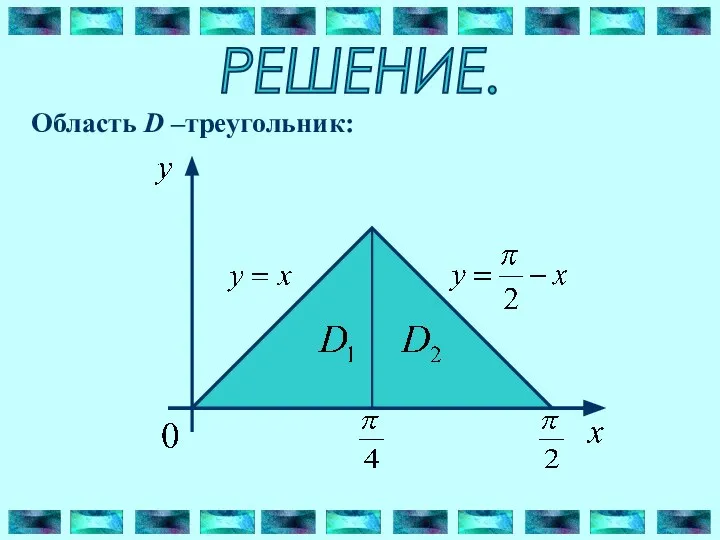
- 10. РЕШЕНИЕ. Область D –треугольник:
- 13. Скачать презентацию








 Векторный анализ
Векторный анализ Доверительные интервалы
Доверительные интервалы Таблицы данных с двумя переменными
Таблицы данных с двумя переменными Функция у-сосх, её свойства и график
Функция у-сосх, её свойства и график Вычисление интегралов средствами MathCad
Вычисление интегралов средствами MathCad Загадочные треугольники
Загадочные треугольники Смежные и вертикальные углы
Смежные и вертикальные углы Решение дифференциальных уравнений с разделяющимися переменными
Решение дифференциальных уравнений с разделяющимися переменными Действия над матрицами. Вычисление определителей второго и третьего порядков
Действия над матрицами. Вычисление определителей второго и третьего порядков Презентация на тему Разность и её значение (1 класс)
Презентация на тему Разность и её значение (1 класс)  Вычитание дробных чисел. 5 класс
Вычитание дробных чисел. 5 класс Презентация на тему Квадратные уравнения. Основные свойства
Презентация на тему Квадратные уравнения. Основные свойства  Теория игр 1819
Теория игр 1819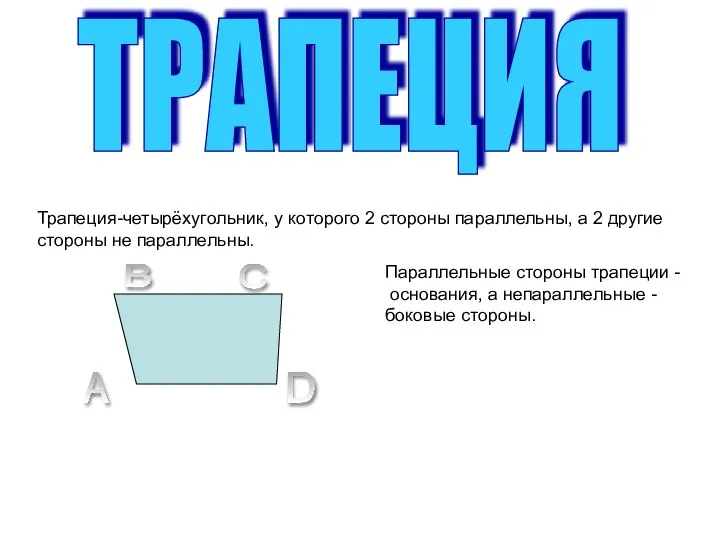 Трапеция
Трапеция Объемы многогранников и тел вращения. Устная работа
Объемы многогранников и тел вращения. Устная работа Решение уравнений
Решение уравнений Презентация на тему Элементы статистики
Презентация на тему Элементы статистики  Влияние личности педагога на формирование ключевых компетентностей и повышения познавательной активности обучающихся
Влияние личности педагога на формирование ключевых компетентностей и повышения познавательной активности обучающихся Измерение параллеппипеда
Измерение параллеппипеда Метод решётчатого умножения. Исследование
Метод решётчатого умножения. Исследование Решение задач
Решение задач Чертежи к уроку Вертикальные углы
Чертежи к уроку Вертикальные углы Практическое. Занятие № 7. Численные методы решения задачи коши
Практическое. Занятие № 7. Численные методы решения задачи коши Решение систем неравенств (8 класс)
Решение систем неравенств (8 класс) Производная. Что это? Зачем это?
Производная. Что это? Зачем это? Буквенная запись свойств действий над числами
Буквенная запись свойств действий над числами Задачи по геометрии
Задачи по геометрии Нахождение неизвестного вычитаемого
Нахождение неизвестного вычитаемого