Содержание
- 2. Задача. Дана система уравнений. Найти значения корней x и y. Перейдём к общему виду системы и
- 3. Метод Крамера основан на вычислении определителя матрицы.
- 4. Для доказательства формул выполним следующие преобразования:
- 5. Аналогичные преобразования выполним для вычисления корня y.
- 6. Составим алгоритм решения. Описать необходимые переменные. 1. Начало 2. Ввести значения матрицы с клавиатуры 3. Вычислить
- 7. Самостоятельно составьте программу на языке TurboPascal. С её помощью найдите корни двух следующих систем уравнений: Предъявите
- 9. Скачать презентацию






 Многоугольники
Многоугольники Показательные уравнения
Показательные уравнения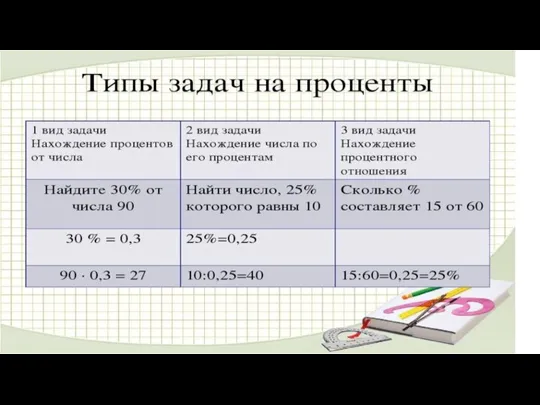 Задачи на проценты
Задачи на проценты Иррациональные уравнения и их системы. Иррациональные неравенства
Иррациональные уравнения и их системы. Иррациональные неравенства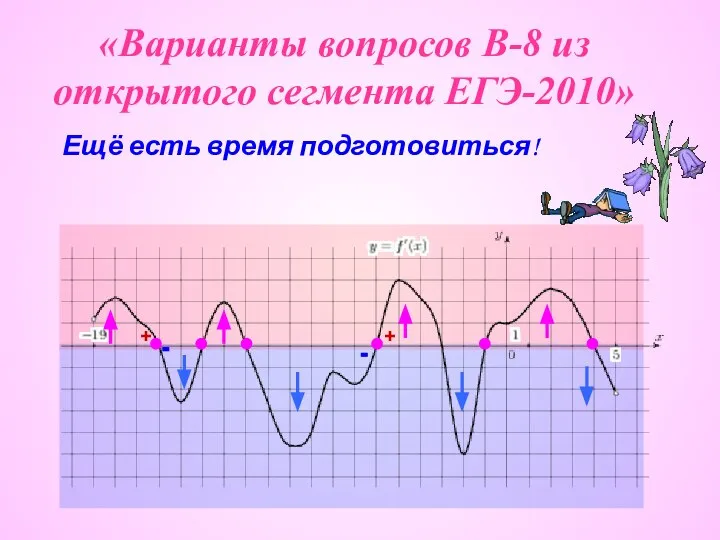 Варианты вопросов В-8 из открытого сегмента ЕГЭ-2010
Варианты вопросов В-8 из открытого сегмента ЕГЭ-2010 Случаи вычитания 11-
Случаи вычитания 11-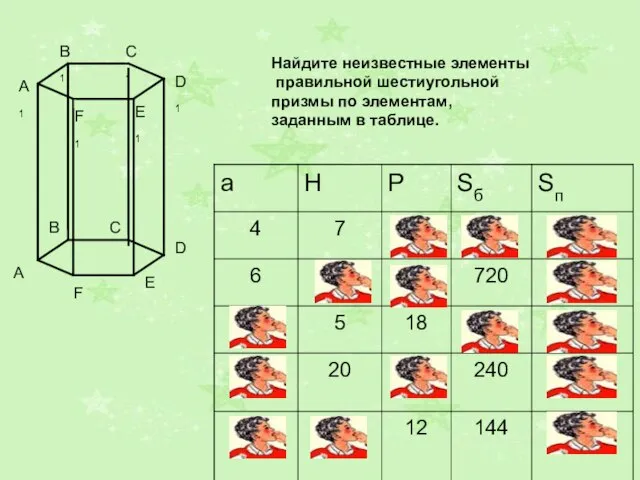 Задачи по призме
Задачи по призме Производная сложной функции
Производная сложной функции Возрастание и убывание функций
Возрастание и убывание функций Десятичные и натуральные логарифмы
Десятичные и натуральные логарифмы Что в центре круга (1 класс)
Что в центре круга (1 класс) Соседи числа
Соседи числа мощность множеств Леонгардт
мощность множеств Леонгардт Ромб. Квадрат
Ромб. Квадрат Логарифмы вокруг нас
Логарифмы вокруг нас Способы решения систем линейных уравнений
Способы решения систем линейных уравнений Проценты. 5 класс
Проценты. 5 класс Решение задач
Решение задач Тригонометрические тождества. Преобразование тригонометрических выражений
Тригонометрические тождества. Преобразование тригонометрических выражений Построение сечений многогранников с применением графического редактора Paint. Интегрированный урок
Построение сечений многогранников с применением графического редактора Paint. Интегрированный урок Все действия с десятичными дробями
Все действия с десятичными дробями Геометрический смысл производной. Практическая работа
Геометрический смысл производной. Практическая работа Уравнение прямой
Уравнение прямой Функция
Функция Длина окружности
Длина окружности Презентация на тему ПОСТРОЕНИЕ ГРАФИКА КВАДРАТИЧНОЙ ФУНКЦИИ
Презентация на тему ПОСТРОЕНИЕ ГРАФИКА КВАДРАТИЧНОЙ ФУНКЦИИ  Тригонометрические уравнения. Найди пару
Тригонометрические уравнения. Найди пару Нахождение числа по его процентам
Нахождение числа по его процентам