Содержание
- 2. Группы, составленные из каких –либо элементов, называются соединениями. Различают три основных вида соединений: размещения, перестановки и
- 3. Комбинаторные задачи делятся на группы: Задачи на перестановки Задачи на размещение Задачи на сочетание
- 4. Перестановки Перестановкой из n элементов называется любое упорядоченное множество, в которое входят по одному разу все
- 5. Запись n! читается так:«эн факториал» Факториал - это произведение всех натуральных чисел от 1 до n
- 6. Размещения Число размещений из n по m находится по формуле: Размещением из n элементов по m
- 7. Сочетания Сочетанием из n элементов по m называется любое подмножество из m элементов, которые принадлежат множеству,
- 8. Особая примета комбинаторных задач – вопрос, который можно сформулировать так, чтобы он начинался словами «Сколькими способами…»
- 10. Скачать презентацию






 Международный день головоломки
Международный день головоломки Серединный перпендикуляр
Серединный перпендикуляр Контрольная работа. Логарифм, логарифмическая функция
Контрольная работа. Логарифм, логарифмическая функция В мире рациональных уравнений
В мире рациональных уравнений Деление на 2
Деление на 2 Теорема о прямой, перпендикулярной к плоскости
Теорема о прямой, перпендикулярной к плоскости Асимптоты. Вертикальная асимптота
Асимптоты. Вертикальная асимптота Задачи и примеры. 1 класс
Задачи и примеры. 1 класс Презентация на тему Письменное умножение на двузначное число (4 класс)
Презентация на тему Письменное умножение на двузначное число (4 класс) 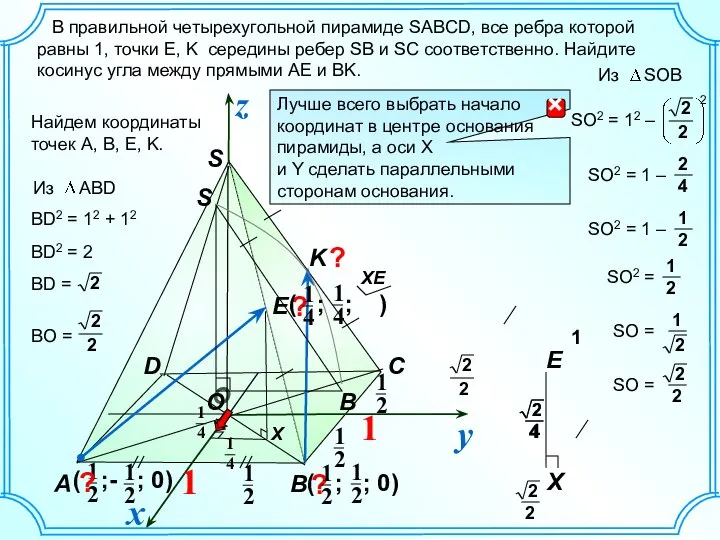 Пирамиды. Решение задач. C 12
Пирамиды. Решение задач. C 12 Таблица истинности
Таблица истинности Предмет и метод статистики
Предмет и метод статистики Урок по геометрии
Урок по геометрии Уравнения, приводимые к квадратным
Уравнения, приводимые к квадратным Кривые второго порядка
Кривые второго порядка Арккосинус. Решение уравнения cos t = a
Арккосинус. Решение уравнения cos t = a Геометрический диктант
Геометрический диктант Множества
Множества Умножение и деление на 3
Умножение и деление на 3 Экономические задачи VI. Задания 1-4, ЕГЭ
Экономические задачи VI. Задания 1-4, ЕГЭ Теория вероятностей в задачах ЕГЭ
Теория вероятностей в задачах ЕГЭ Подготовка к ВПР
Подготовка к ВПР Движение. Осевая симметрия
Движение. Осевая симметрия Презентация на тему Измерение длин отрезков
Презентация на тему Измерение длин отрезков  Построение графиков тригонометрических функций
Построение графиков тригонометрических функций Решите примеры
Решите примеры Математическое обеспечение и администрирование информационных систем
Математическое обеспечение и администрирование информационных систем Математические игры
Математические игры