Содержание
- 2. Литература С.М. Никольский «Алгебра и начала анализа: Учебник для 10 класса общеобразовательных учреждений» §2 п. 2.7
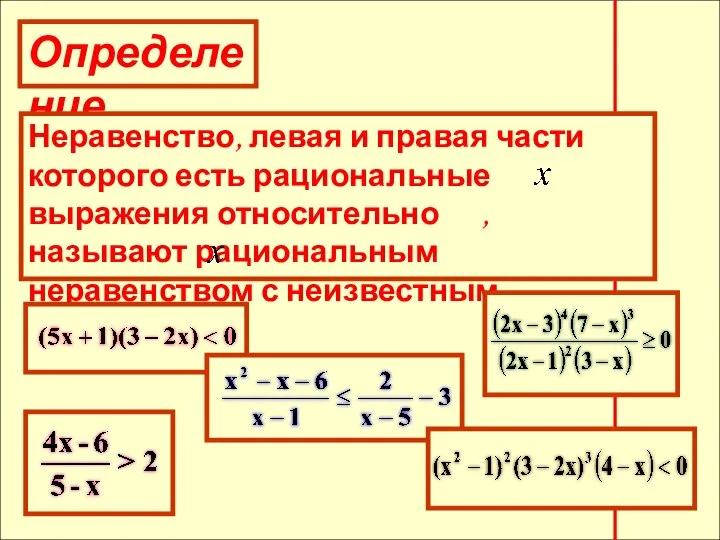
- 4. Определение
- 7. + - + - +
- 9. Метод интервалов для решения неравенств вида , , , , где , , , то есть
- 10. 3. Над промежутком справа от наибольшего нуля многочлена поставить знак «+», так как на этом промежутке
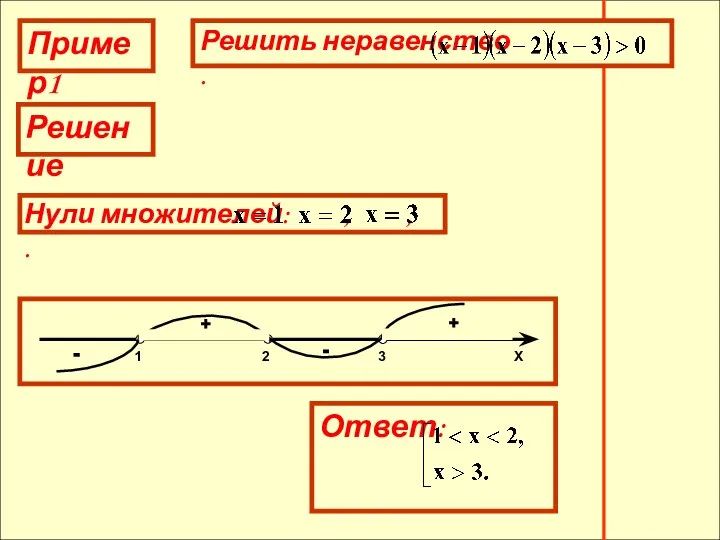
- 11. Пример1 Решение + - + -
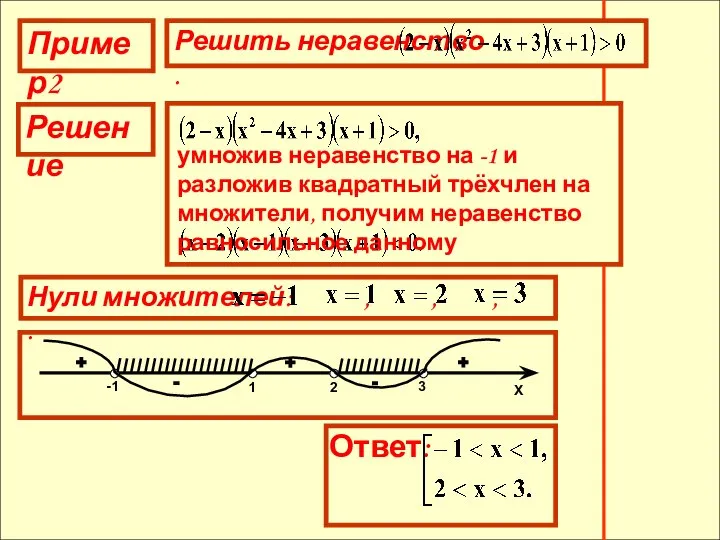
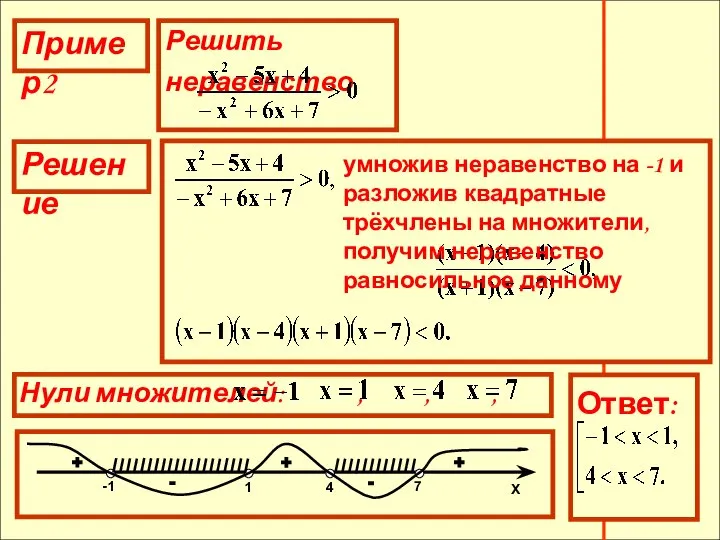
- 12. Пример2 Решение умножив неравенство на -1 и разложив квадратный трёхчлен на множители, получим неравенство равносильное данному
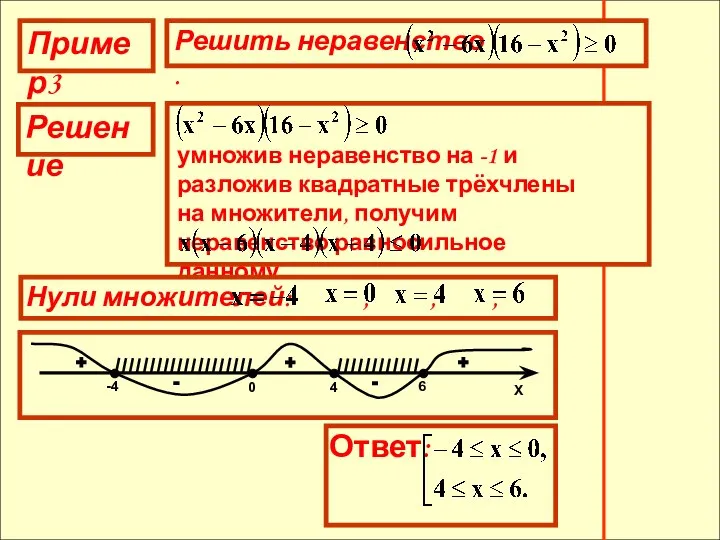
- 13. Пример3 Решение умножив неравенство на -1 и разложив квадратные трёхчлены на множители, получим неравенство равносильное данному
- 14. Пример4 Решение Нули множителей: , , , , , . + + + + - -
- 15. Общий метод интервалов для решения неравенств вида , , , ,где , если не все различны.
- 16. Общий метод интервалов для решения неравенств вида , , , ,где , если не все различны.
- 17. Решение Нули множителей: , , , . + + - - +
- 18. + - - +
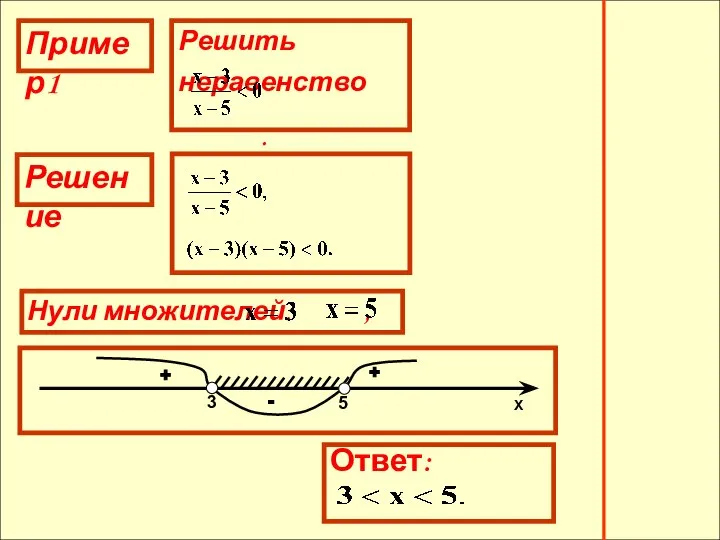
- 20. Нули множителей: , . + + -
- 21. умножив неравенство на -1 и разложив квадратные трёхчлены на множители, получим неравенство равносильное данному Нули множителей:
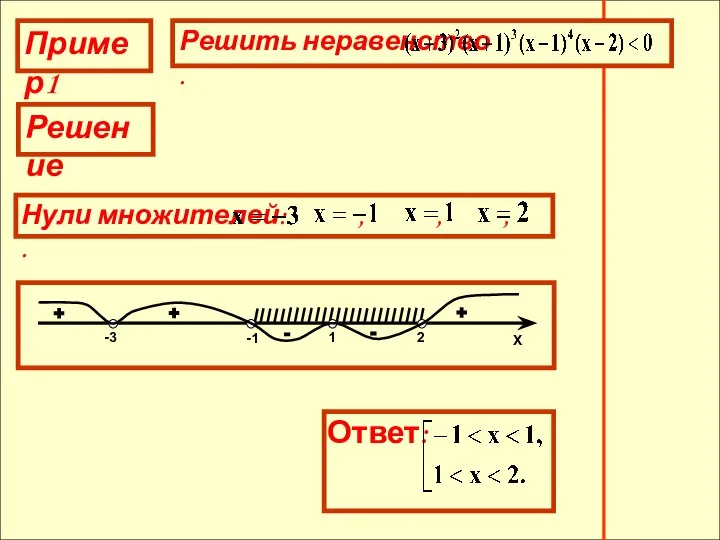
- 22. Нули множителей: , , , . + - + - +
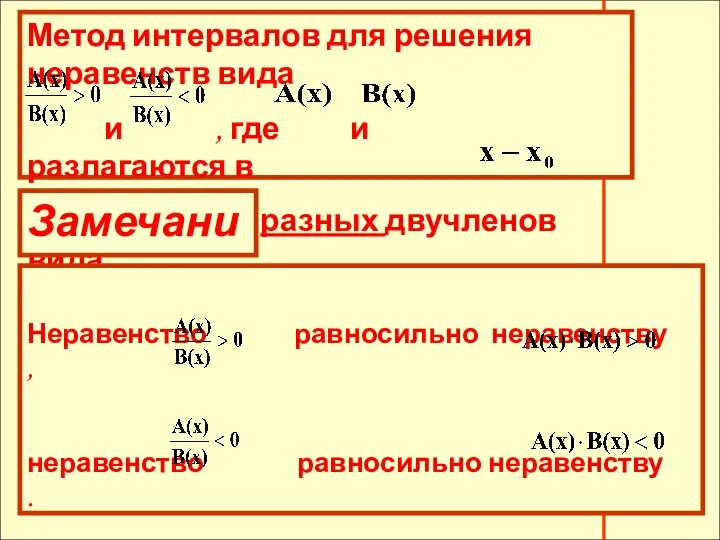
- 23. Метод интервалов для решения неравенств вида и , где и разлагаются в произведения двучленов, где в
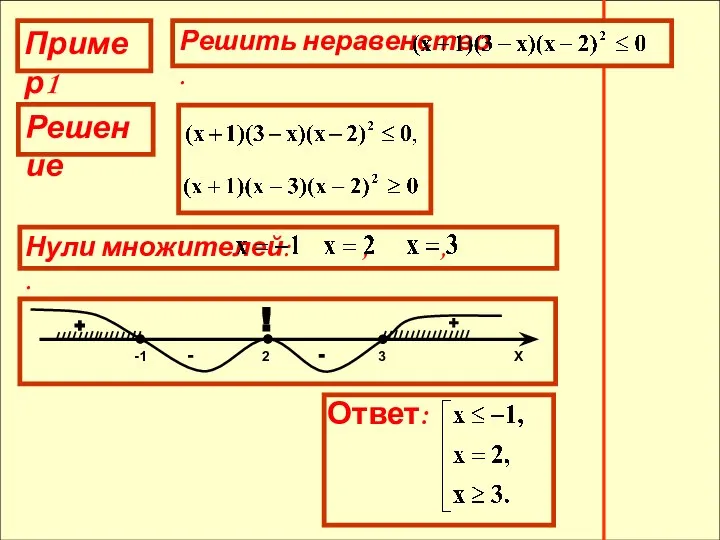
- 24. Нули множителей: , , . + - - +
- 27. Нули числителя: , . Нули знаменателя: , , . + + + - - -
- 29. Скачать презентацию

















 Дифференцирование показательной и логарифмической функций
Дифференцирование показательной и логарифмической функций В стране геометрических фигур (форма, размер, цвет)
В стране геометрических фигур (форма, размер, цвет) Арифметический квадратный корень
Арифметический квадратный корень Натуральные числа и дроби. Урок 1
Натуральные числа и дроби. Урок 1 Круговая окружность
Круговая окружность Среднее арифметическое
Среднее арифметическое Презентация на тему Перевод целых чисел в 2, 8, 16-ую системы счисления
Презентация на тему Перевод целых чисел в 2, 8, 16-ую системы счисления  Устно. Вычисления
Устно. Вычисления Презентация на тему Умножение и деление десятичной дроби на 10, 100, 1000 и т.д.
Презентация на тему Умножение и деление десятичной дроби на 10, 100, 1000 и т.д.  lobachevsky
lobachevsky Сложение и вычитание положительных десятичных дробей
Сложение и вычитание положительных десятичных дробей Золотое сечение
Золотое сечение Арифметическая прогрессия
Арифметическая прогрессия Взаимно обратные числа
Взаимно обратные числа Теорема Пифагора
Теорема Пифагора Статистические графики
Статистические графики ложение комплексных чисел. Вычитание комплексных чисел
ложение комплексных чисел. Вычитание комплексных чисел Булева алгебра
Булева алгебра Зимующие птицы. Дети 5 лет
Зимующие птицы. Дети 5 лет Числа от 1 до 100. Умножение и деление. Закрепление
Числа от 1 до 100. Умножение и деление. Закрепление Задания по математике (5 класс, часть 7)
Задания по математике (5 класс, часть 7) Геометрический смысл производной
Геометрический смысл производной Векторы на плоскости
Векторы на плоскости Интерактивный тренажёр. Сложение и вычитание в пределах первого десятка. 3 уровень
Интерактивный тренажёр. Сложение и вычитание в пределах первого десятка. 3 уровень Синус, косинус и тангенс угла
Синус, косинус и тангенс угла Курс по математике ОГЭ 2021
Курс по математике ОГЭ 2021 Проценты (1)
Проценты (1) Деление обыкновенных дробей
Деление обыкновенных дробей