Слайд 2Комбинации
Определение.
Различные группы, составленные из каких- либо элементов (предметов) и отличающиеся одна

от другой либо числом элементов, либо самими элементами, либо их порядком, называют комбинациями
Слайд 4Правило суммы
Если некоторый объект А может быть выбран из совокупности объектов m

способами, а другой объект В может быть выбран n способами, то выбрать либо А, либо В можно m+n способами.
Слайд 5Пример 1
В качестве призов для участников школьного вернисажа решено было купить акварельные

краски и наборы фломастеров, чтобы наградить каждого участника либо набором акварельных красок, либо набором фломастеров. В магазине в продаже оказалось 7 различных наборов красок и 12 различных наборов фломастеров. Сколько различных подарков можно сделать при имеющемся ассортименте?
Слайд 6Решение
Число выборов набора красок m=7, число выборов набора фломастеров n=12, тогда число

выборов либо набора красок, либо набора фломастеров равно m+n=7+12=19.
Ответ: 19.
Слайд 7При использовании правила суммы
в приведенной формулировке нужно следить, чтобы ни один из

способов выбора объекта А не совпадал со способом выбора объекта В. Если такие совпадения есть, то число способов выбора либо А, либо В составляет m+n-k, где k- число совпадений
Слайд 8Пример 2
Все ученики класса занимаются двумя видами спорта- легкой атлетикой и волейболом.

Волейболом занимаются 12 учеников, а легкой атлетикой- 19, причем 5 учеников, занимающихся легкой атлетикой, занимаются также и волейболом. Сколько учеников в классе?
Слайд 9Решение:
Число учеников, занимающихся волейболом m=12, число учеников, занимающихся легкой атлетикой n=19, число

учеников, занимающихся обоими видами спорта k=5, значит число учеников класса равно m+n-k=12+19-5=26
Ответ: 26.
Слайд 10Правило произведения
Если объект А можно выбрать из совокупности объектов m способами и

после каждого такого выбора объект В можно выбрать n способами, то пара объектов (А, В) в указанном порядке может быть выбрана mn способами
Слайд 11Пример 3
В качестве призов для участников школьного вернисажа решено было купить акварельные

краски и наборы фломастеров, чтобы наградить каждого участника одним набором акварельных красок и одним набором фломастеров. В магазине в продаже оказалось 7 различных наборов красок и 12 различных наборов фломастеров. Сколько различных подарков можно сделать при имеющемся ассортименте?
Слайд 12Решение
Число выборов набора красок m=7, число выборов набора фломастеров n=12, тогда число

выборов одного набора красок и одного набора фломастеров равно m∙n=7∙12=84.
Ответ: 84.
Слайд 13Задача 4
Имеется 6 пар перчаток различных цветов. Сколькими способами можно выбрать из

них одну перчатку на левую руку, а одну на правую руку так, чтобы перчатки были разных цветов?
Слайд 14Задача 5
Сколькими способами можно выбрать одну гласную и одну согласную буквы из

слова «тропа»?
Слайд 15Размещения
- это комбинации, составленные из n различных элементов по m элементов

в каждой и отличающиеся одна от другой либо составом элементов, либо порядком следования элементов.
Слайд 16Пример 4
Сколько различных комбинаций можно создать из букв А, В и С

по 2 буквы в каждой?
Слайд 17Решение:
АВ, АС, ВА, ВС, СА,СВ
Ответ: 6.

Слайд 19Пример 5
В классе 10 учебных предметов и 5 разных уроков в день.

Сколькими способами могут быть распределены уроки в день?
Слайд 20Пример 6
Научное общество состоит из 25 человек. Надо выбрать президента общества, вице-

президента, ученого секретаря и казначея. Сколькими способами может быть сделан этот выбор, если каждый член общества может занимать лишь один пост?
Слайд 21Перестановки
- это комбинации, состоящие из одних и тех же n различных элементов

и отличающиеся только порядком их расположения.
Слайд 22Пример 7
Сколько трехзначных чисел можно составить из цифр 1, 2, 3, если

каждая цифра входит в изображение числа только один раз?
Слайд 23Решение:
123, 132, 213, 231, 312,321
Ответ: 6.

Слайд 25Пример 8
Сколько девятизначных чисел можно написать девятью разными цифрами 1, 2, 3,

4, 5, 6, 7, 8, 9.
Слайд 26Пример 9
Сколькими способами можно разместить 12 лиц за столом, на котором поставлено

12 приборов?
Слайд 27Сочетания
- это комбинации, составленные из n различных элементов по m элементов в

каждой и отличающиеся одна от другой хотя бы одним элементом
Слайд 28Пример 10
Сколькими способами можно выбрать две детали из ящика содержащего 5 деталей?

Слайд 29Решение:
Пусть детали пронумерованы:
1, 2, 3, 4, 5. Тогда возможны следующие исходы
12,

13, 14, 15, 23, 24, 25, 34, 35, 45.
Ответ: 10.
















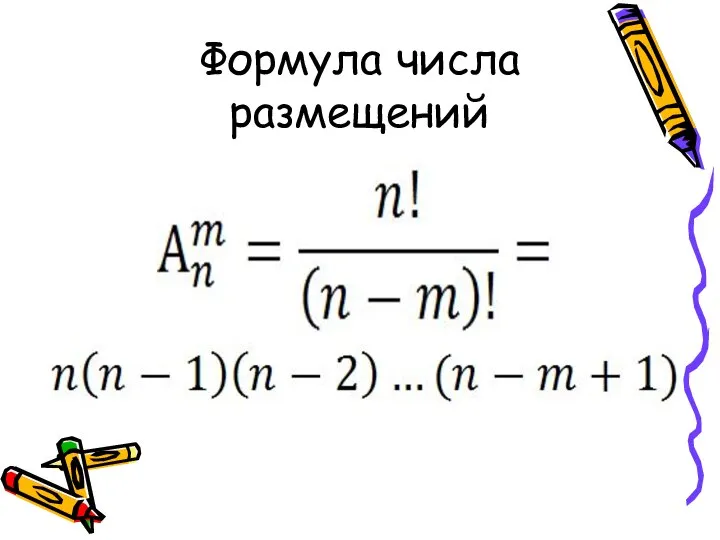





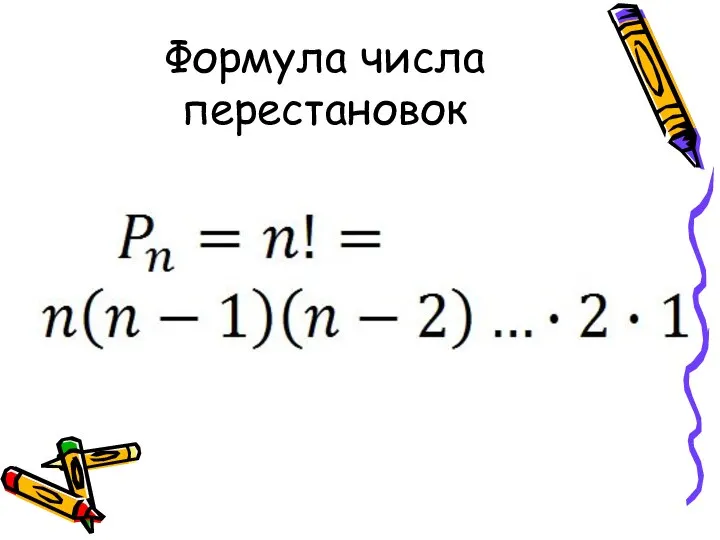





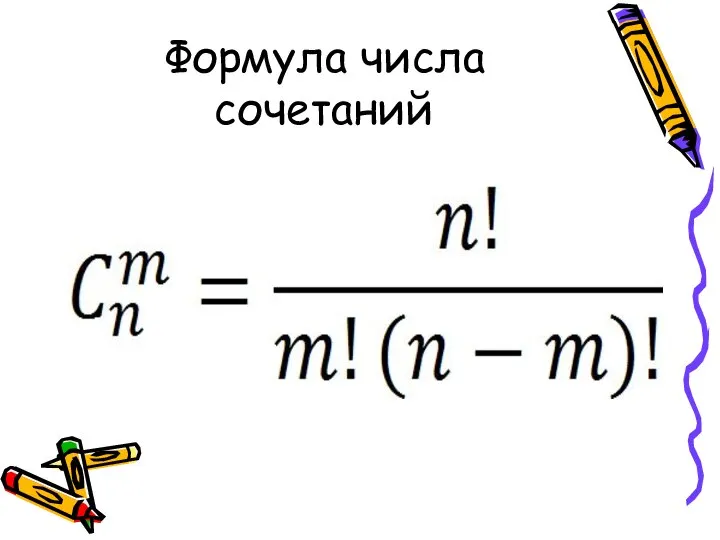
 Векторы. 9 класс
Векторы. 9 класс Задачи на построение сечений
Задачи на построение сечений Взаимно-обратные операции
Взаимно-обратные операции Уменьшаемое, вычитаемое, разность
Уменьшаемое, вычитаемое, разность Конус, его элементы и виды конусов
Конус, его элементы и виды конусов Многоугольники. Параллелограмм. 8 класс
Многоугольники. Параллелограмм. 8 класс Математическая разминка
Математическая разминка Прибавление числа 6 с переходом через десяток
Прибавление числа 6 с переходом через десяток Линейные неравенства. 8 класс
Линейные неравенства. 8 класс Чтение и запись многозначных чисел. Класс миллионов. Класс миллиардов
Чтение и запись многозначных чисел. Класс миллионов. Класс миллиардов Случаи вычитания
Случаи вычитания Окружность. Задачи на построение
Окружность. Задачи на построение Логарифм числа
Логарифм числа Уменьшаемое, вычитаемое, разность
Уменьшаемое, вычитаемое, разность Правильные многоугольники
Правильные многоугольники Проценты. Три задачи
Проценты. Три задачи Векторы в пространстве
Векторы в пространстве Решение логических задач с помощью нескольких таблиц. Вычислительные таблицы
Решение логических задач с помощью нескольких таблиц. Вычислительные таблицы Проценты
Проценты 1.3. Определители
1.3. Определители Простые и составные числа (дистант)
Простые и составные числа (дистант) Обобщенный эвристический алгоритм
Обобщенный эвристический алгоритм Общие приемы решения уравнений
Общие приемы решения уравнений Тест по теме функция
Тест по теме функция Презентация на тему Решение неравенств с одной переменной (11 класс)
Презентация на тему Решение неравенств с одной переменной (11 класс)  Решение систем неравенств с одной переменной. 8 класс
Решение систем неравенств с одной переменной. 8 класс Целые числа. Рациональные числа
Целые числа. Рациональные числа Вычисление объемов тел вращения
Вычисление объемов тел вращения