Слайд 2 Многогранник или полиэдр — поверхность, составленная из многоугольников, которые ограничивают некоторое пространство.

Слайд 3 Цель ─ расширить представление о геометрических фигурах на примере невыпуклых многогранников.

Задачи:
1.Выявить признак невыпуклости многогранников.
2.Определить основные свойства невыпуклых многогранников.
3.Выяснить, каково применение невыпуклых многогранников в повседневной жизни.
Гипотетический вопрос:
Возможно ли создать что-то полезное в виде невыпуклого многогранника?
Слайд 4 Невыпуклые многогранники обладают такими гранями, плоскости которых разделяют фигуру на две

части, расположенные по обе стороны данной плоскости.
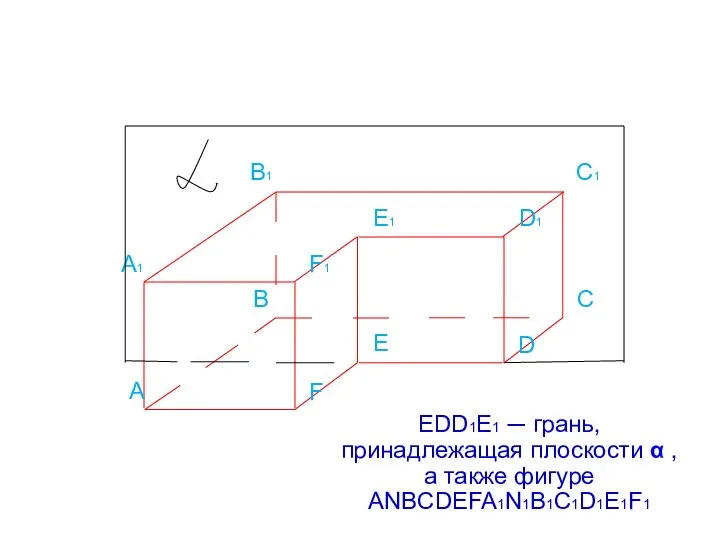
Слайд 5А
B
С
D
E
F
A1
B1
C1
D1
E1
F1
EDD1E1 ─ грань, принадлежащая плоскости α , а также фигуре ANBCDEFA1N1B1C1D1E1F1
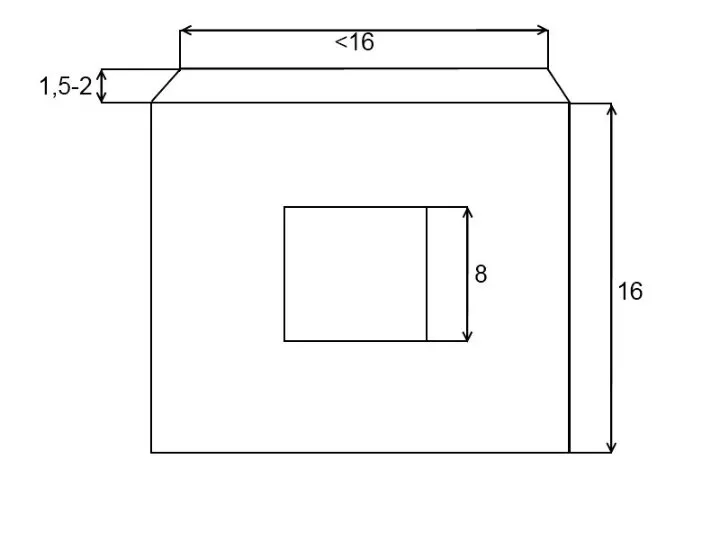
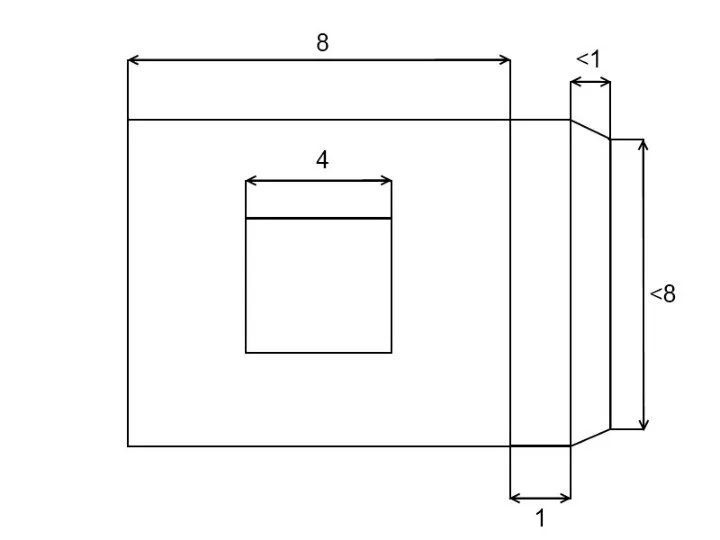
Слайд 23 Затраченный материал:
1) 8 листов для черчения формата А4
2) клей

Расчётная площадь поверхности:
Sполн. пов. = Sпов. куба. + Sотв.
Слайд 24Выводы:
1.Признак невыпуклости многогранника
доказан.
2.Невыпуклые многогранники являются своеобразными геометрическими фигурами.
3.В форме невыпуклых

многогранников существует множество предметов повседневной жизни.
Слайд 25Заключение.
В нашем мире существует много примеров воплощения креативных, интересных и полезных

идей в жизнь и быт человека. Одним из таких примеров может служить невыпуклый многогранник, в виде которого на сегодняшний день существует немало объектов повседневной жизни.




















 Скрипт параллелограм
Скрипт параллелограм Компьютерное решение задач по теме Арифметическая прогрессия
Компьютерное решение задач по теме Арифметическая прогрессия Составные задачи
Составные задачи Средняя линия треугольника
Средняя линия треугольника Комплексные числа и действия над ними
Комплексные числа и действия над ними Не итерируемые или неизменяемые объекты
Не итерируемые или неизменяемые объекты Математический магазин
Математический магазин В мире треугольников. (1) 7 класс
В мире треугольников. (1) 7 класс Примеры использования OpenMP. Вычисление определенного интеграла
Примеры использования OpenMP. Вычисление определенного интеграла Решение тригонометрических уравнений
Решение тригонометрических уравнений Презентация на тему Деление обыкновенных дробей
Презентация на тему Деление обыкновенных дробей  Математика. Фигуры
Математика. Фигуры Параллельные прямые
Параллельные прямые Умножение обыкновенных дробей
Умножение обыкновенных дробей Презентация на тему Применение решения задач на проценты
Презентация на тему Применение решения задач на проценты  Деление обыкновенных дробей
Деление обыкновенных дробей Площади и объемы
Площади и объемы Урок математики по теме: Сложение и вычитание в пределах 20
Урок математики по теме: Сложение и вычитание в пределах 20 Презентация на тему История возникновения геометрии
Презентация на тему История возникновения геометрии  Математические шифровки
Математические шифровки Вторая производная и ее физический смысл
Вторая производная и ее физический смысл Свойства равнобедренного треугольника. Решение задач
Свойства равнобедренного треугольника. Решение задач Подготовка к контрольной работе. Изображение промежутков и запись их в виде неравенств
Подготовка к контрольной работе. Изображение промежутков и запись их в виде неравенств Презентация на тему Нахождение значений тригонометрических функций с помощью таблиц Брадиса
Презентация на тему Нахождение значений тригонометрических функций с помощью таблиц Брадиса  Производная и первообразная
Производная и первообразная Презентация на тему Счёт предметов (1 класс)
Презентация на тему Счёт предметов (1 класс)  Применение теоремы Пифагора
Применение теоремы Пифагора Презентация на тему Десятичные дроби (5 класс)
Презентация на тему Десятичные дроби (5 класс)