Статистическая обработка массива однородных величин. Практическое занятие 2

По статистическим данным определяем хср – среднее значение и S – среднее квадратичное отклонение для всего массива статистических данных рассчитываются по общим формулам:
; (4)
На основании условий и признаков, при которых следует ожидать появление того или иного закона распределения, а также по виду графика эмпирической функции распределения, производится предварительный выбор закона распределения исследуемой случайной величины.
Наиболее распространенные в теории надежности законы распределения случайных величин
нормальный закон распределения
закон распределения Вейбулла
экспоненциальный закон распределения

В зависимости от принятого закона распределения случайных величин производиться расчет его параметров:
для двухпараметрического закона нормального распределения а = хср, σ = S;
для двухпараметрического закона распределения Вейбулла по формуле
(5)
определяется параметр V и затем по таблице 1 находится величина m.
В случае отсутствия соответствующего значения в таблице задача может быть решена подбором значения m, преобразующего уравнение (5) в тождество.
Второй параметр λ определяется из уравнения:
для однопараметрического экспоненциального закона распределения при хср ≈ S ,

Таблица 1.
Зависимость между параметрами V и m для распределения Вейбулла
V m V m V m V m
0,36 3,03 0,58 1,78 0,80 1,26 1,50 0,68
0,38 2,85 0,60 1,72 0,85 1,18 1,60 0,64
0,40 2,70 0,62 1,66 0,90 1,11 1,80 0,59
0,42 2,55 0,64 1,60 0,95 1,05 2,00 0,54
0,44 2,42 0,66 1,54 1,00 1,00 2,20 0,50
0,46 2,31 0,68 1,49 1,05 0,95 2,40 0,47
0,48 2,20 0,70 1,45 1,10 0,91 2,60 0,45
0,50 2,10 0,72 1,41 1,15 0,87 3,00 0,41
0,52 2,01 0,74 1,37 1,20 0,84 3,50 0,37
0,54 1,93 0,76 1,33 1,30 0,78 4,00 0,35
0,56 1,85 0,78 1,29 1,40 0,73 5,00 0,31

Проверка соответствия выбранного закона распределения случайных величин имеющимся статистическим данным
Для проверки соответствия выбранного закона распределения случайных
величин имеющимся статистическим данным необходимо произвести проверку графическим способом, по критерию Колмогорова или по критерию χ2 (хи – квадрат).
Во всех случаях для проверки необходимо определить теоретические значения количества отказов для каждого из интервалов.
Расчет производиться по формуле
Расчет производиться для середины соответствующего интервала
хр = ti ср

Проверка соответствия выбранного закона распределения случайных величин имеющимся статистическим данным
Наиболее прост и нагляден графический способ проверки.
На графике изменения частостей (гистограмме или полигоне распределения), построенном по статистическим данным, строиться аналогичный график по полученным теоретическим данным. Совпадение графиков свидетельствует о правильности выбора закона распределения.
Проверка по критерию Колмогорова производиться в следующей последовательности:
1. Для всех интервалов определяются значения модуля разности между эмпирическими и теоретическими накопленными частотами по формуле
2. Определяется максимальное значение di max и величина λк:
, где

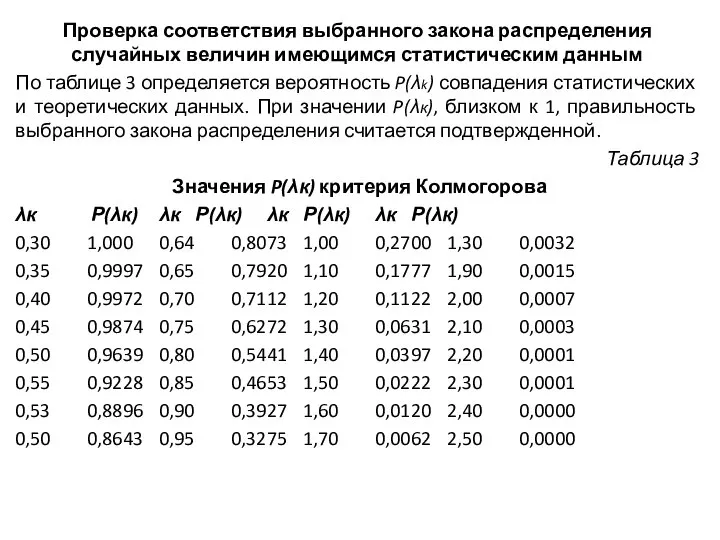
Проверка соответствия выбранного закона распределения случайных величин имеющимся статистическим данным
По таблице 3 определяется вероятность P(λk) совпадения статистических и теоретических данных. При значении P(λк), близком к 1, правильность выбранного закона распределения считается подтвержденной.
Таблица 3
Значения P(λк) критерия Колмогорова
λк Р(λк) λк Р(λк) λк Р(λк) λк Р(λк)
0,30 1,000 0,64 0,8073 1,00 0,2700 1,30 0,0032
0,35 0,9997 0,65 0,7920 1,10 0,1777 1,90 0,0015
0,40 0,9972 0,70 0,7112 1,20 0,1122 2,00 0,0007
0,45 0,9874 0,75 0,6272 1,30 0,0631 2,10 0,0003
0,50 0,9639 0,80 0,5441 1,40 0,0397 2,20 0,0001
0,55 0,9228 0,85 0,4653 1,50 0,0222 2,30 0,0001
0,53 0,8896 0,90 0,3927 1,60 0,0120 2,40 0,0000
0,50 0,8643 0,95 0,3275 1,70 0,0062 2,50 0,0000

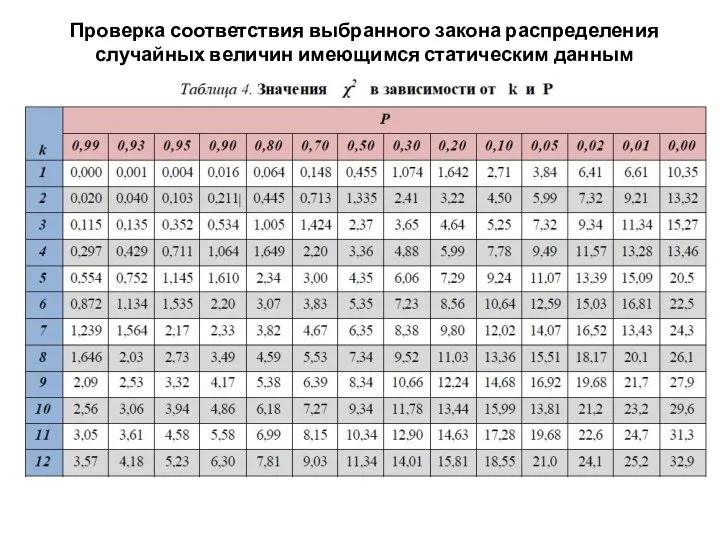
Проверка соответствия выбранного закона распределения случайных величин имеющимся статистическим данным
Критерий согласия хи-квадрат применяется при большом количестве опытных данных и в случаях, если теоретические значения параметров функции распределения неизвестны. Сравнение статистических данных с теоретическими значениями функции распределения производиться следующим образом:
Производиться группировка (объединение) интервалов таким образом, чтобы в каждом из интервалов было бы не менее 4-6 отказов.
2. Определяется мера расхождения χ2 по формуле
Определяется число степеней свободы k по формуле
k = r – m – 1,
где r – количество интервалов после группировки;
m – количество параметров в законе распределения (для распределения Вейбулла - λ и m).

Проверка соответствия выбранного закона распределения случайных величин имеющимся статическим данным
3. По найденным значениям χ2 и k по таблице 4 находиться вероятность Р того, что величина, имеющая распределение хи – квадрат с k степенями свободы, превзойдет полученное значение χ2.
Если эта вероятность мала (0,1-0,2), то принятое теоретическое распределение должно быть отвергнуто как неправдоподобное. Большие значения вероятности (больше 0,7-0,8) свидетельствуют, что допущены какие-то систематические ошибки или погрешности при предварительной обработке статистических данных.
Таким образом, при 0,2 ≤ Р ≤ 0,7 считается, что принятая гипотеза распределения отказов, определенных по принятой теории распределения, соответствует статистическим данным.

Проверка соответствия выбранного закона распределения случайных величин имеющимся статическим данным

Пример (продолжение)
Задание: Произвести статистическую обработку массива однородных экс- периментальных данных об отказах УЭЦН.
Исходные данные (наработка, сут):
340 774 279 517 470 934 76 397
570 221 679 983 756 701 277 498
824 432 386 506 597 641 209 214
272 384 411 729 689 682 540 650
561 716 404 575 88 189 124 721

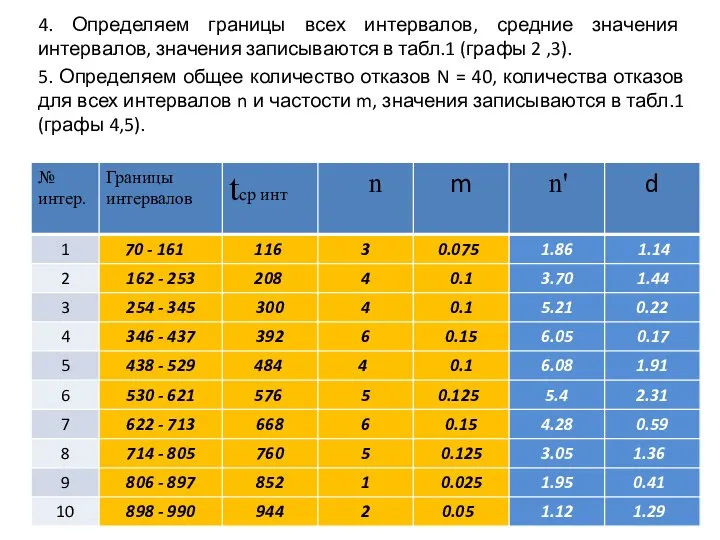
4. Определяем границы всех интервалов, средние значения интервалов, значения записываются в табл.1 (графы 2 ,3).
5. Определяем общее количество отказов N = 40, количества отказов для всех интервалов n и частости m, значения записываются в табл.1 (графы 4,5).
табл.1

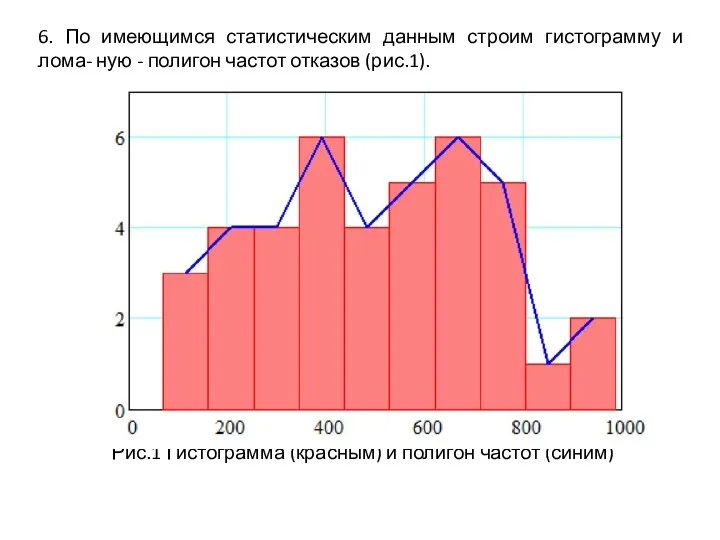
6. По имеющимся статистическим данным строим гистограмму и лома- ную - полигон частот отказов (рис.1).
Рис.1 Гистограмма (красным) и полигон частот (синим)

7. Определяем величину среднего значения
, tср = 500,4 сут.
8. Определяем величины среднего значения среднеквадратичного отклонения S:
, S = 228,7 сут.
9. Исходя из рис. 1 выбираем закон распределения Вейбулла
и определяем его параметр.
Вводим вспомогательный параметр V, численное значение которого находим через
tср и S.
V = S / tср = 0,457
По таблице зависимости между параметрами V и m распределения Вейбулла определяем m = 2,3 .

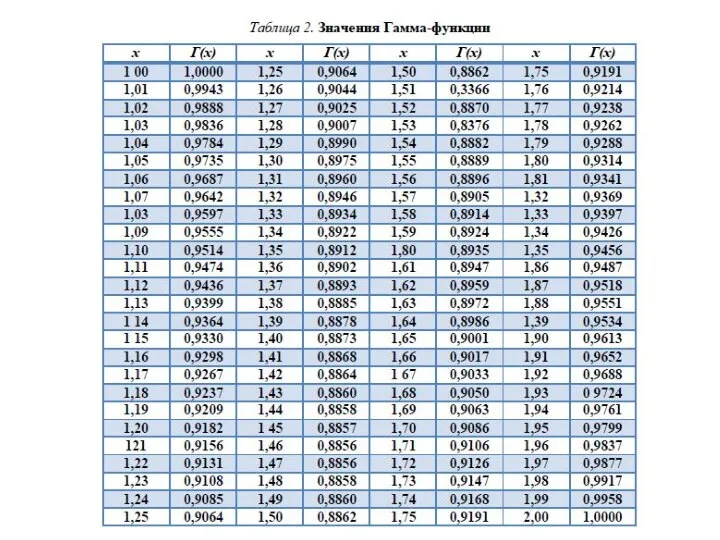
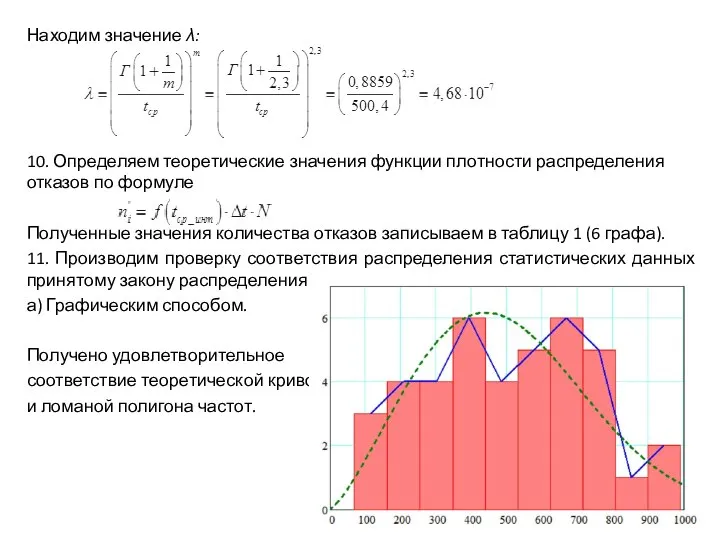
Находим значение λ:
10. Определяем теоретические значения функции плотности распределения отказов по формуле
Полученные значения количества отказов записываем в таблицу 1 (6 графа).
11. Производим проверку соответствия распределения статистических данных принятому закону распределения.
а) Графическим способом.
Получено удовлетворительное
соответствие теоретической кривой
и ломаной полигона частот.

б) По критерию Колмогорова. Определяем накопленное количество отказов для каждого интервала по статистическим и теоретическим данным, а также d- модули их разности.
Результаты записываются в табл.1 (графа 7).
По справочникам определяется вероятность P(λk) = 0.9985.
Полученное значение близко к единице, что подтверждает правильность выбранного теоретического закона распределения.