Системы линейных уравнений СЛУ

3.1.2. Метод Крамера
i
Из предыдущего имеем:

3.1.3. Метод Гаусса
Последовательно исключаем переменные, используя элементарные преобразования, пока не приведем матрицу А к диагональному виду

Пример

Пример (метод Крамера)

Пример (метод Гаусса)

4.1. Виды систем линейных уравнений.
4. Исследование системы линейных уравнений
Решение системы — любой вектор-столбец X, для которого выполняется равенство AX=B.
Как определить
<= Теорема Кронекера-Капелли
но сначала…

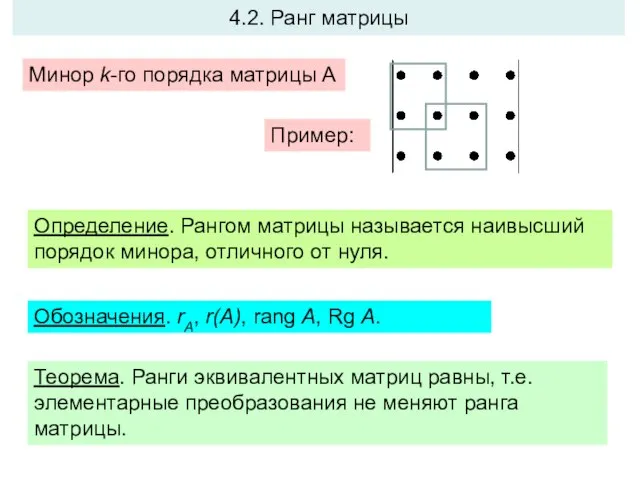
4.2. Ранг матрицы
Минор k-го порядка матрицы А
Пример:
Определение. Рангом матрицы называется наивысший порядок минора, отличного от нуля.
Обозначения. rA, r(A), rang A, Rg A.
Теорема. Ранги эквивалентных матриц равны, т.е. элементарные преобразования не меняют ранга матрицы.

Теорема. Ранг матрицы равен наибольшему числу её линейно независимых строк или столбцов.

r(A)=min{k, l}, где
k — максимальное число линейно независимых строк А,
l — максимальное число линейно независимых столбцов А.
Следствия для квадратной матрицы.
Если определитель квадратной матрицы равен нулю, то её строки (или столбцы) линейно зависимы.
Если строки (или столбцы) квадратной матрицы линейно зависимы, то её определитель равен нулю.
Способы вычисления ранга матрицы.
Метод окаймляющих миноров.
Метод элементарных преобразований.

Метод элементарных преобразований.
С помощью элементарных преобразований получить в левом верхней углу единичную (или треугольную) матрицу.
Нулевые строки переставлять вниз, а нулевые столбцы - вправо.
Ранг матрицы равен порядку полученной единичной или треугольной матрицы.
Пример:

4.3. Теорема Кронекера-Капелли
Пусть АХ=В некоторая СЛУ, A-nxm тогда
1) Если r(A)=r(A|B), то система совместная
1а) Если r(A)=r(A|B)=m, то система совместная и определенная
1б) Если r(A)=r(A|B)
2) Если r(A)
Нет строк типа 0=5
Сколько неизвестных, столько и разных уравнений => решение единственное
Неизвестных больше, чем уравнений => решение общее, зависит от С
ЕСТЬ строки типа 0=5

Замечания об однородной системе AX = 0.
Она всегда совместна (всегда есть нулевое решение).
Нулевое решение существует, только если r(A) < n, или det A = 0.
Порядок исследования системы линейных уравнений.
1. Исследование совместности:
(а) однородная - неоднородная?
(б) теорема Кронекера-Капелли.
2. Исследование неопределённости:
(а) r(A) = n?

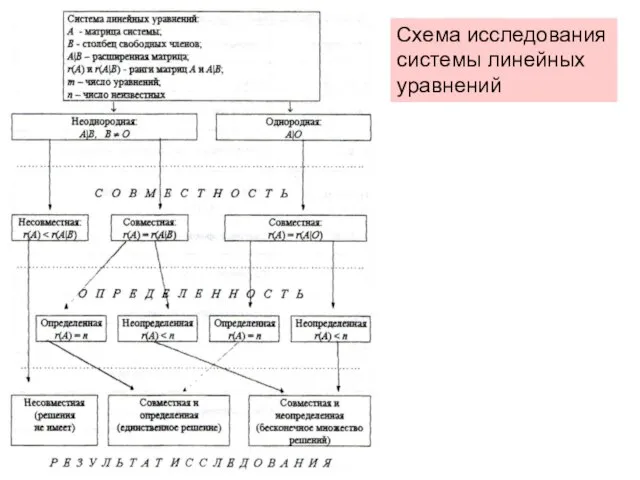
Схема исследования системы линейных уравнений

Пример
Проверяем на совместность. Если совместна, то решаем
r(A) = 2, r(A|B) = 3, r(A) ≠ r(A|B) => система несовместна и решения не имеет.

Ещё пример
r(A) = 3, r(A|B) = 3, n = 3 => система совместная и определённая. Продолжаем…
(2; 3; -1)