Слайд 2Базовые понятия
Определения
Правильная пирамида — это пирамида, у которой боковые рёбра равны, а

в основании лежит правильный n-угольник
Правильный тетраэдр — это треугольная пирамида, все рёбра которой равны.
Объём пирамиды вычисляется по формуле: V = 1/3 Sh, где S — площадь основания, h — высота пирамиды
Прямая призма — это призма, боковые рёбра которой перпендикулярны плоскостям оснований.
Правильная n-угольная призма — это прямая призма, основанием которой служит правильный n-угольник.
Параллелепипед — это призма, основанием которой служит параллелограмм.
Объём призмы вычисляется по формуле: V = Sh, где S — площадь основания призмы, h — её высота.
Слайд 5Как будем это рисовать?
Алгоритм
1) рисуем основание пирамиды;
2) строим центр основания, проводя

медианы треугольника или диагонали квадрата;
3) из центра ведём вверх высоту и отмечаем на ней вершину пирамиды;
4) соединяем вершину пирамиды с вершинами основания.
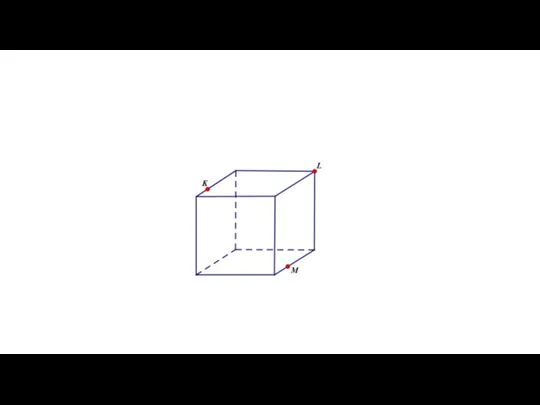
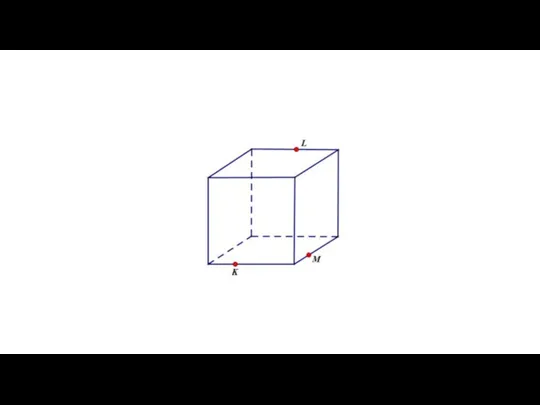
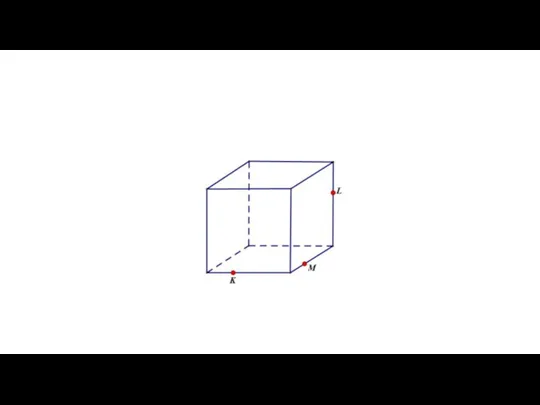
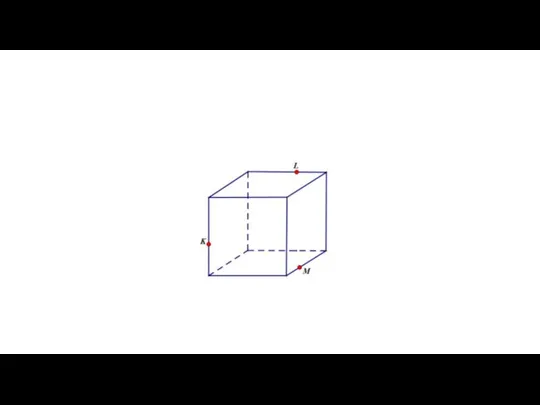
Слайд 6Взаимное расположение прямых в пространстве
Существует три варианта взаимного расположения двух прямых в

пространстве: прямые могут быть
пересекающимися,
параллельными
скрещивающимися.
Слайд 7Угол между скрещивающимися прямыми
Скрещивающиеся прямые не пересекаются. Можно ли в таком случае

говорить об угле между ними?
Слайд 10Параллельность прямой и плоскости
Как распознать случай параллельности прямой и плоскости?
Для этого

имеется замечательно простое утверждение.
Признак параллельности прямой и плоскости. Если прямая l параллельна некоторой прямой, лежащей в плоскости, то прямая l параллельна этой плоскости.
Слайд 11Давайте посмотрим, как работает этот признак.
Пусть ABCA1B1C1 — треугольная призма, в

которой проведена плоскость A1BC
Слайд 12ОЧЕНЬ ВАЖНАЯ ТЕОРЕМА
Теорема о пересечении двух плоскостей, одна из которых проходит через

прямую, параллельную другой плоскости.
Слайд 13Для чего она нужна?
Пример
В правильной четырёхугольной пирамиде ABCDS (с вершиной S) точка

M — середина ребра SC. Постройте сечение пирамиды плоскостью ABM
Слайд 14Перпендикулярность прямой и плоскости
Определение. Прямая называется перпендикулярной плоскости, если она перпендикулярна любой

прямой, лежащей в этой плоскости.
Слайд 15Мы же не будем перебирать все прямые?!
Признак перпендикулярности прямой и плоскости.
Если

прямая перпендикулярна двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна этой плоскости.
Слайд 16Пример
Докажите, что в правильной треугольной пирамиде скрещивающиеся рёбра перпендикулярны.

Слайд 20Задача
Докажите, что в правильной треугольной пирамиде скрещивающиеся рёбра перпендикулярны.

Слайд 22Задача
В правильном тетраэдре найдите угол между боковым ребром и плоскостью основания

Слайд 33Тоже оч важно
если две различные плоскости имеют общую точку, то они пересекаются

по прямой, проходящей через эту точку.
Слайд 35Задача
Найдите угол между двумя гранями правильного тетраэдра.























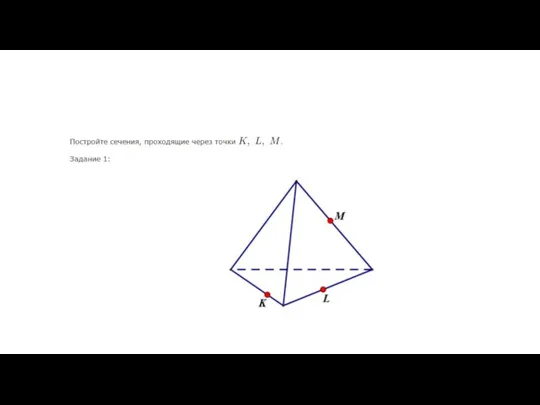
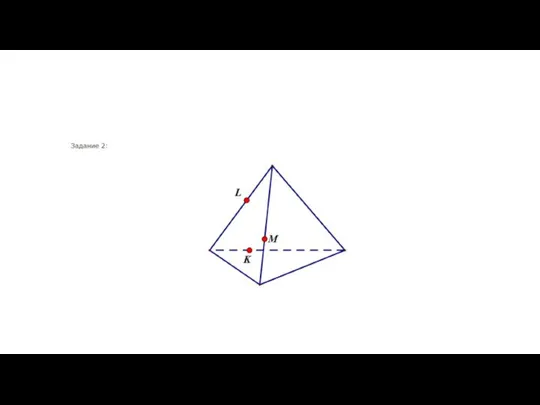
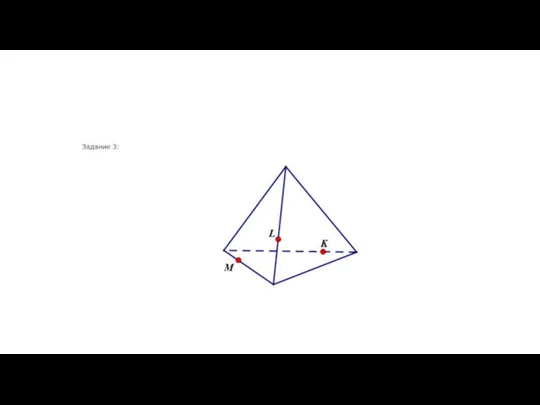
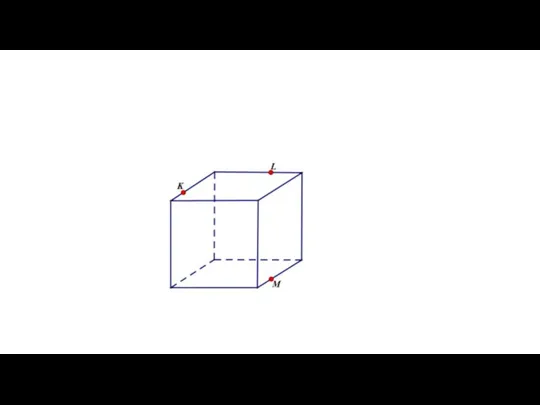




 Нумерационные случаи сложения и вычитания чисел второго десятка
Нумерационные случаи сложения и вычитания чисел второго десятка Массивы. Работа с массивами
Массивы. Работа с массивами Виды треугольников. 5 класс
Виды треугольников. 5 класс Сложение и вычитание многочленов
Сложение и вычитание многочленов Интегрирование на подмножествах (Кратный интеграл)
Интегрирование на подмножествах (Кратный интеграл)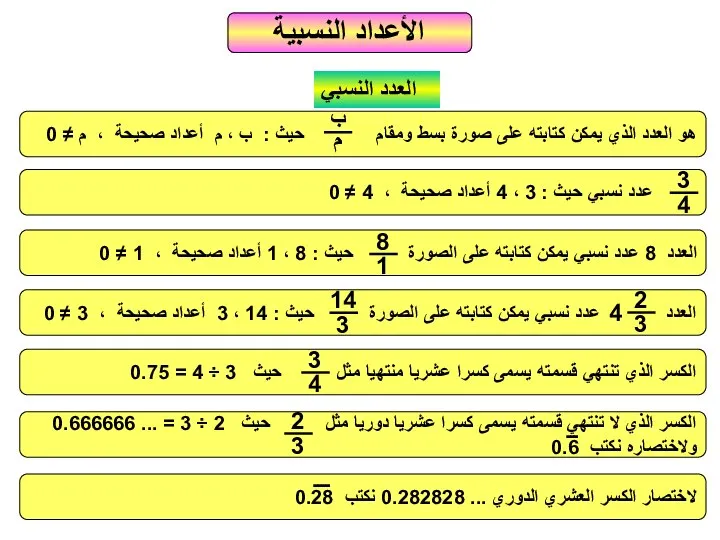 الأعداد انسبية
الأعداد انسبية Решение неравенств методом интервалов
Решение неравенств методом интервалов Интегрирование некоторых классов функций
Интегрирование некоторых классов функций Презентация на тему Среднее арифметическое (5 класс)
Презентация на тему Среднее арифметическое (5 класс)  Специальная теория относительности
Специальная теория относительности Применение производной для исследования функции на монотонность и экстремумы
Применение производной для исследования функции на монотонность и экстремумы Геометрическая прогрессия
Геометрическая прогрессия Математическая викторина (начальная школа)
Математическая викторина (начальная школа) Сокращение дробей
Сокращение дробей Алгоритмы в нашей жизни
Алгоритмы в нашей жизни Выражения с переменными
Выражения с переменными Л11 Производная функции
Л11 Производная функции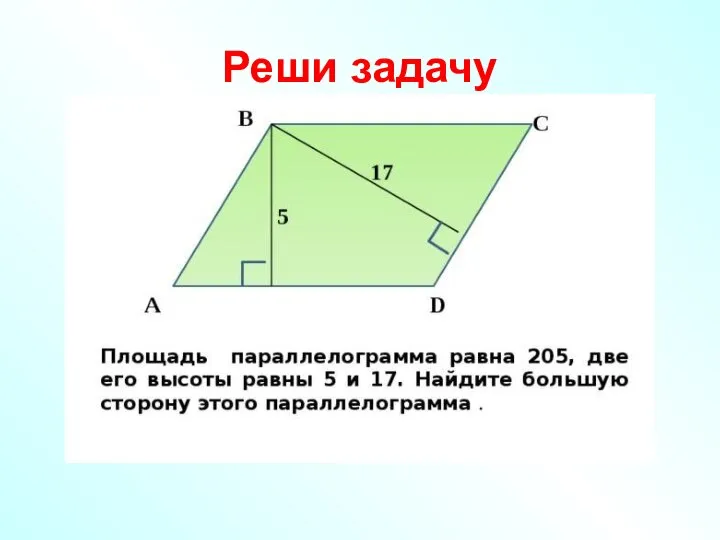 Решение задач на площадь параллелограмма
Решение задач на площадь параллелограмма Действительные числа и преобразования алгебраических выражений (домашнее задание)
Действительные числа и преобразования алгебраических выражений (домашнее задание) Графическое решение уравнений
Графическое решение уравнений Презентация на тему Векторы в пространстве
Презентация на тему Векторы в пространстве  Коэффициент корреляции
Коэффициент корреляции Прибавление числа 6 с переходом через десяток
Прибавление числа 6 с переходом через десяток Решение задач
Решение задач Математический калейдоскоп
Математический калейдоскоп Музей геометрии
Музей геометрии Своя Игра! Математика
Своя Игра! Математика Прямая и обратная пропорциональные зависимости
Прямая и обратная пропорциональные зависимости