Решение задач. Определение по графикам формулы функций

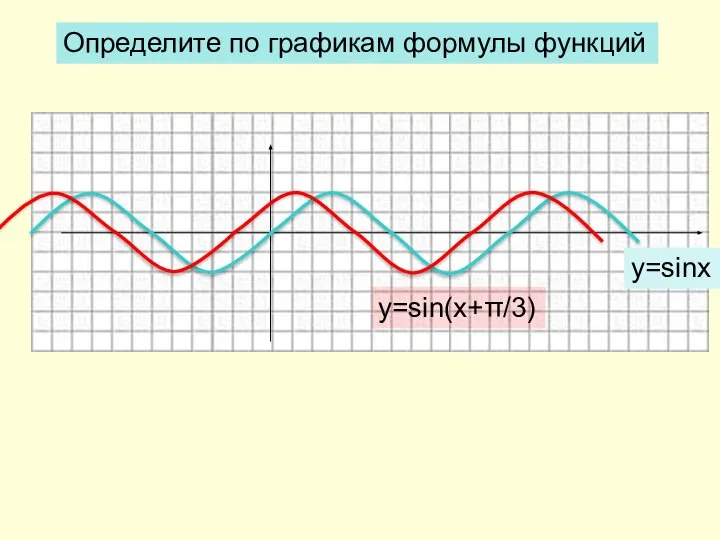
Определите по графикам формулы функций
y=sinx
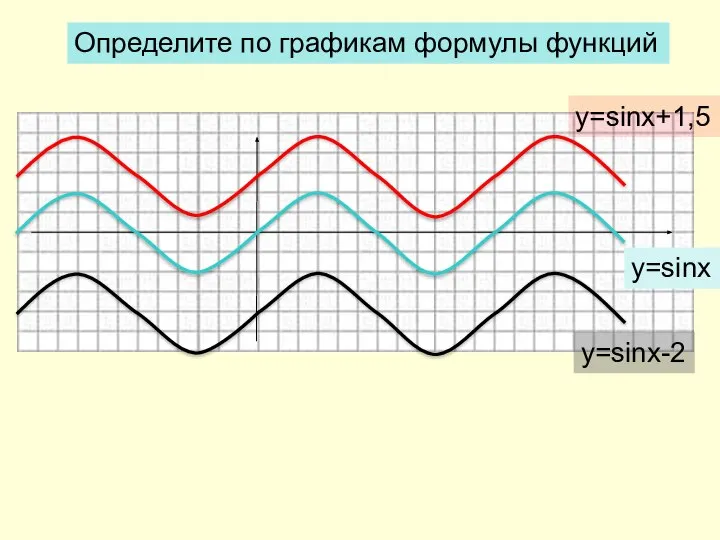
y=sin(x+π/3)

Определите по графикам формулы функций
y=sinx
y=sinx+1,5
y=sinx-2

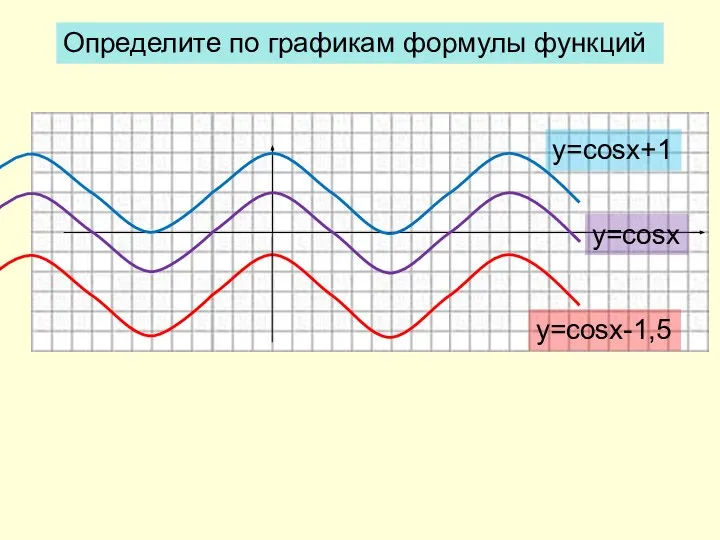
Определите по графикам формулы функций
y=cosx
y=cosx+1
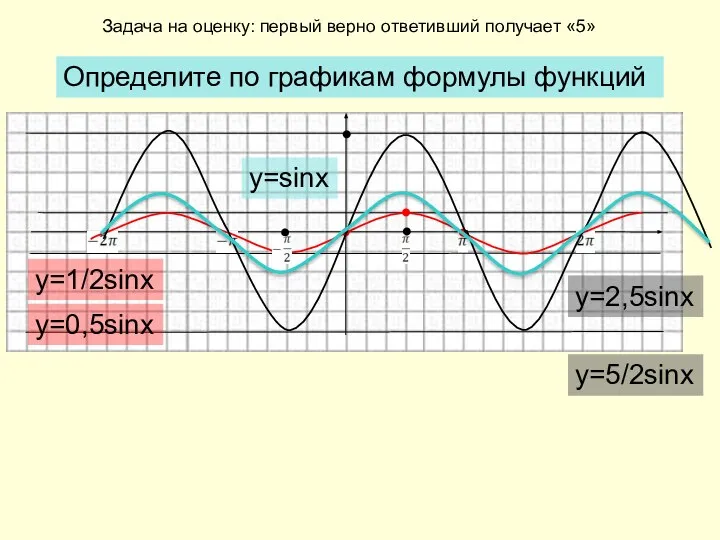
y=cosx-1,5

Определите по графикам формулы функций
y=1/2sinx
y=2,5sinx
y=sinx
Задача на оценку: первый верно ответивший получает «5»
y=0,5sinx
y=5/2sinx

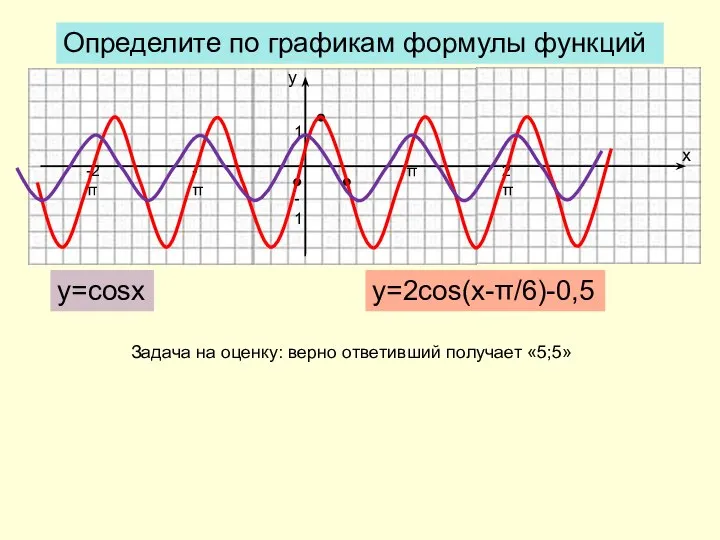
Определите по графикам формулы функций
y=cosx
y=2cos(x-π/6)-0,5
Задача на оценку: верно ответивший получает «5;5»

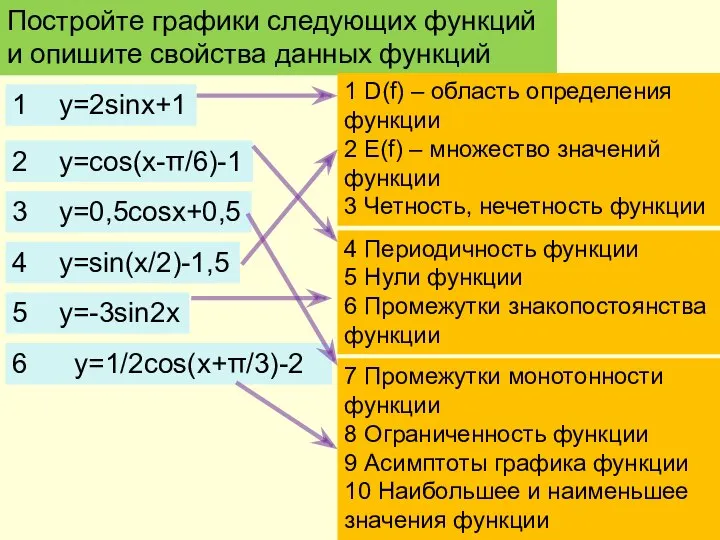
Постройте графики следующих функций и опишите свойства данных функций
1 D(f) – область определения функции
2 E(f) – множество значений функции
3 Четность, нечетность функции
4 Периодичность функции
5 Нули функции
6 Промежутки знакопостоянства функции
7 Промежутки монотонности функции
8 Ограниченность функции
9 Асимптоты графика функции
10 Наибольшее и наименьшее значения функции

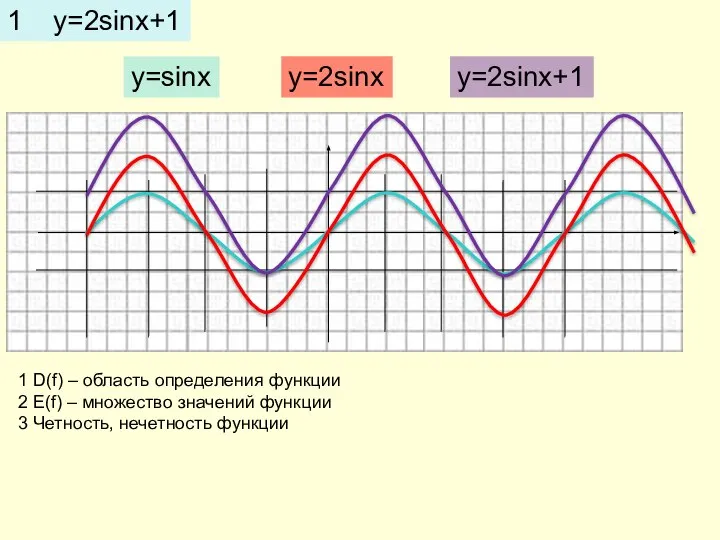
1 y=2sinx+1
y=2sinx
y=sinx
y=2sinx+1
1 D(f) – область определения функции
2 E(f) – множество значений функции
3 Четность, нечетность функции

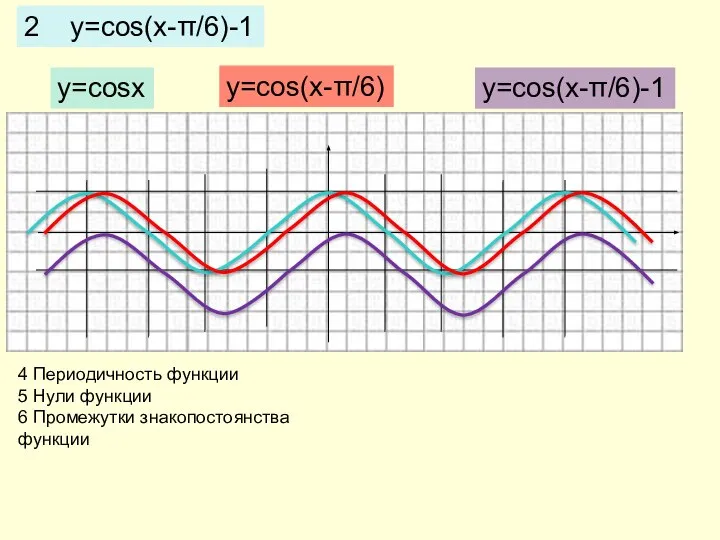
2 y=cos(x-π/6)-1
y=cosx
y=cos(x-π/6)
y=cos(x-π/6)-1
4 Периодичность функции
5 Нули функции
6 Промежутки знакопостоянства функции

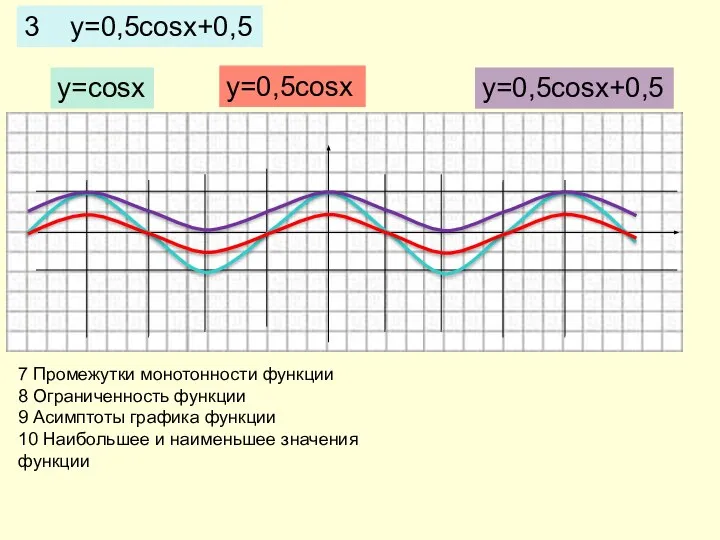
3 y=0,5cosx+0,5
y=cosx
y=0,5cosx
y=0,5cosx+0,5
7 Промежутки монотонности функции
8 Ограниченность функции
9 Асимптоты графика функции
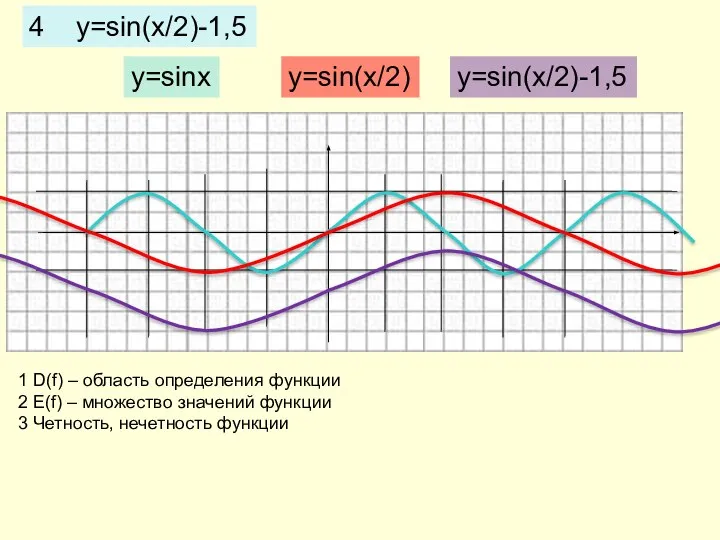
10 Наибольшее и наименьшее значения функции

4 y=sin(x/2)-1,5
y=sinx
y=sin(x/2)
y=sin(x/2)-1,5
1 D(f) – область определения функции
2 E(f) – множество значений функции
3 Четность, нечетность функции

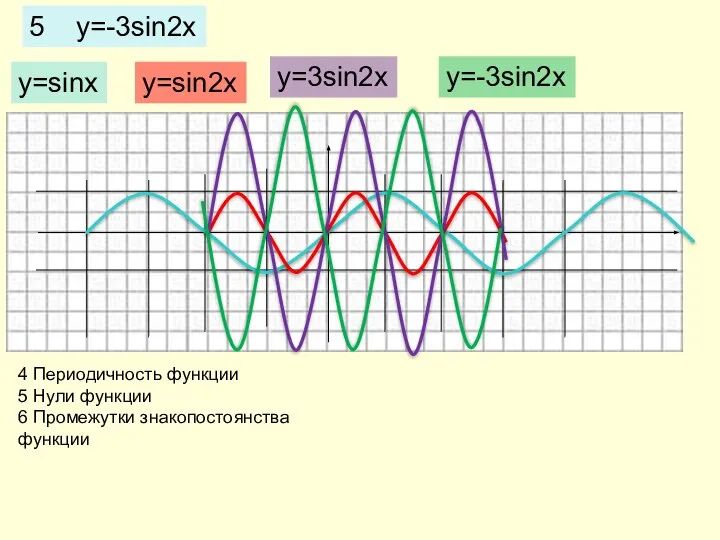
5 y=-3sin2x
y=sinx
y=sin2x
y=3sin2x
y=-3sin2x
4 Периодичность функции
5 Нули функции
6 Промежутки знакопостоянства функции

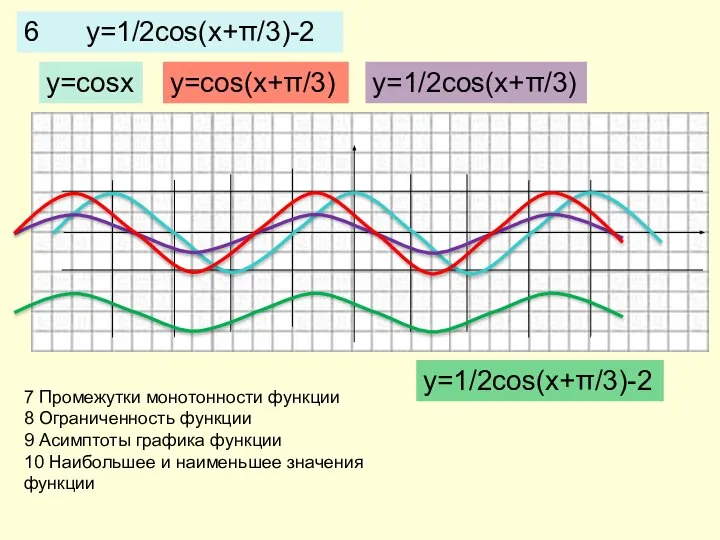
6 y=1/2cos(x+π/3)-2
y=cosx
y=cos(x+π/3)
y=1/2cos(x+π/3)
y=1/2cos(x+π/3)-2
7 Промежутки монотонности функции
8 Ограниченность функции
9 Асимптоты графика функции
10 Наибольшее и наименьшее значения функции