Слайд 2ПЛАН.
Посмотреть задания которые встречаются на ОГЭ
Решение.
Сложно-ли?

Слайд 4ЗАДАЧА №1.
Какое наименьшее количество дуг нужно заказать, чтобы расстояние между соседними дугами

было не более 60 см?
Длина теплицы составляет 4 м = 400 см. Рассчитаем количество дуг для теплицы, соблюдая условие: расстояние между соседними дугами меньше или равно 60 см. Разделим 400 на 60. Получится 6 дуг и в остатке 40 см. Учитывая две крайние дуги, получается:6 + 2 = 8 (дуг).
Слайд 5ЗАДАНИЕ №2.
Сколько упаковок плитки необходимо купить для дорожек между грядками, если она

продается в упаковках по 6 штук?
Из условия задачи имеем, что грядок в теплице планируется 3. Дорожек будет 2. Длина дорожки совпадает с длиной теплицы, то есть 4 м = 400 см. Ширина дорожки — 40 см. Найдем площадь двух дорожек. 2 * 40 * 400 = 32000 (кв. см).
Площадь одной плитки: 20 * 20 = 400 (кв. см).
32000 : 400 = 80 (штук) плиток нужно купить для двух дорожек.
80 :6 = 13 (остаток 2).
Понадобится 13 + 1 = 14 упаковок плитки.
Слайд 6ЗАДАНИЕ №3.
Найдите ширину теплицы. Ответ дайте в метрах с точностью до десятых.
Дуги
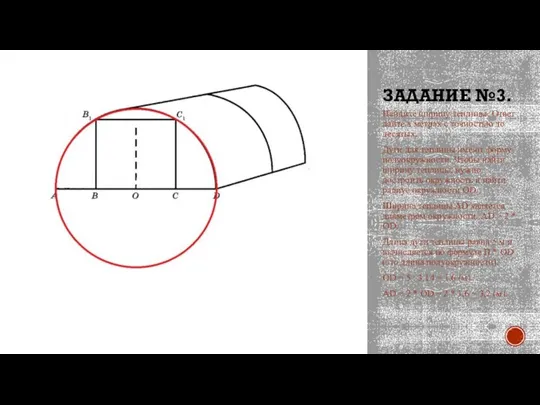
для теплицы имеют форму полуокружности. Чтобы найти ширину теплицы, нужно достроить окружность и найти радиус окружности OD.
Ширина теплицы AD является диаметром окружности. AD = 2 * OD.
Длина дуги теплицы равна 5 м и вычисляется по формуле П * OD (это длина полуокружности).
OD = 5 : 3,14 = 1,6 (м).
AD = 2 * OD = 2 * 1,6 = 3,2 (м).
Слайд 7ЗАДАНИЕ №4.
Найдите ширину центральной грядки, если она в два раза больше ширины

узкой грядки. Ответ дайте в сантиметрах с точностью до десятых.
Ширина теплицы 3,2 м = 320 см. В теплице есть 2 дорожки по 40 см и три грядки. Пусть ширина узкой грядки х см, тогда широкой грядки — 2х см.
Составим уравнение 2х + х + х + 2 * 40 = 320 и решим его.
4х + 80 = 320,
4х = 320 — 80,
4х = 240,
х = 60 (см) — ширина узкой грядки.
Найдем ширину центральной грядки (широкой). 2х = 2 * 60 = 120 (см).
Слайд 8ЗАДАНИЕ №5
Найдите высоту входа в теплицу. Ответ дайте в сантиметрах.
Чтобы найти высоту
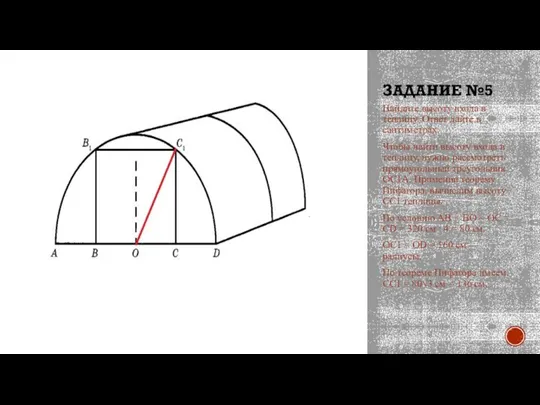
входа в теплицу, нужно рассмотреть прямоугольный треугольник OC1A. Применив теорему Пифагора, вычислим высоту CC1 теплицы.
По условию AB = BO = OC = CD = 320 см : 4 = 80 см.
ОС1 = OD = 160 см — радиусы.
По теореме Пифагора имеем: СС1 = 80√3 см = 136 см.
Слайд 9СЛОЖНО-ЛИ?
Разобрав эту задачу, мы поняли , что ничего сложного в этом нет.









 Обращение обыкновенной дроби в десятичную
Обращение обыкновенной дроби в десятичную Векторный порядок. Дифференциальные операции второго порядка
Векторный порядок. Дифференциальные операции второго порядка ДУ и численные методы. Системы дифференциальных уравнений. 2 семестр. Лекция 8
ДУ и численные методы. Системы дифференциальных уравнений. 2 семестр. Лекция 8 Методы оптимальных решений
Методы оптимальных решений Презентация на тему Решение неравенств методом интервалов (9 класс)
Презентация на тему Решение неравенств методом интервалов (9 класс)  Презентация на тему Многочлены
Презентация на тему Многочлены  Представьте в виде неправильной дроби
Представьте в виде неправильной дроби Логарифмические неравенства
Логарифмические неравенства Презентация на тему Понятие одночлена стандартный вид одночлена (7 класс)
Презентация на тему Понятие одночлена стандартный вид одночлена (7 класс)  Расстояния и углы
Расстояния и углы Задача на тему Прогрессия
Задача на тему Прогрессия Бесконечно убывающая геометрическая прогрессия
Бесконечно убывающая геометрическая прогрессия Площадь. Площадь прямоугольника. 5 класс
Площадь. Площадь прямоугольника. 5 класс ЛЕКЦИЯ_6
ЛЕКЦИЯ_6 Презентация на тему Двугранный угол
Презентация на тему Двугранный угол  Виды углов. Измерение углов
Виды углов. Измерение углов Циклоида, эпициклоида
Циклоида, эпициклоида Килограмм. Математика. 1 класс
Килограмм. Математика. 1 класс Решение квадратных уравнений
Решение квадратных уравнений Квадратные уравнения. Устная разминка
Квадратные уравнения. Устная разминка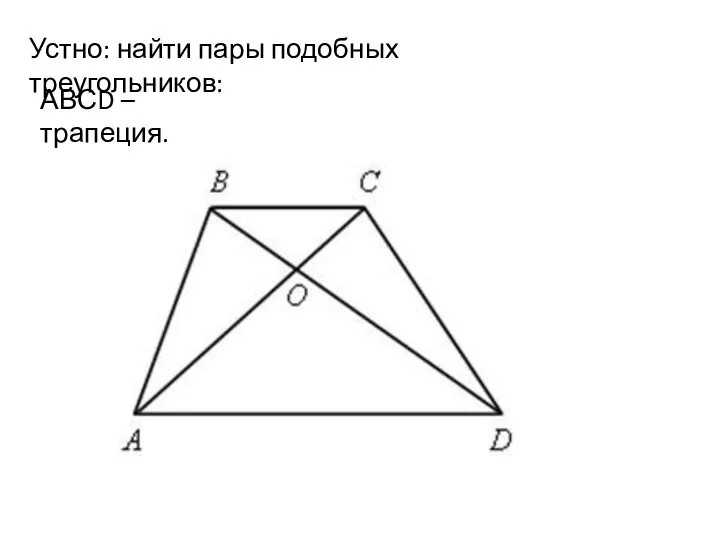 Признак подобия треугольников. Урок 32
Признак подобия треугольников. Урок 32 Как помочь ребенку понять математику. Вебинар 2
Как помочь ребенку понять математику. Вебинар 2 Применение интеграла к решению практических задач
Применение интеграла к решению практических задач Исследование функций и построение графиков
Исследование функций и построение графиков Презентация на тему Решение задач по теме "Пирамида" 10 класс
Презентация на тему Решение задач по теме "Пирамида" 10 класс  Объём произвольного тела вращения
Объём произвольного тела вращения Планиметрия. Что такое геометрия?
Планиметрия. Что такое геометрия? Окружность. Задачи на построение
Окружность. Задачи на построение