Содержание
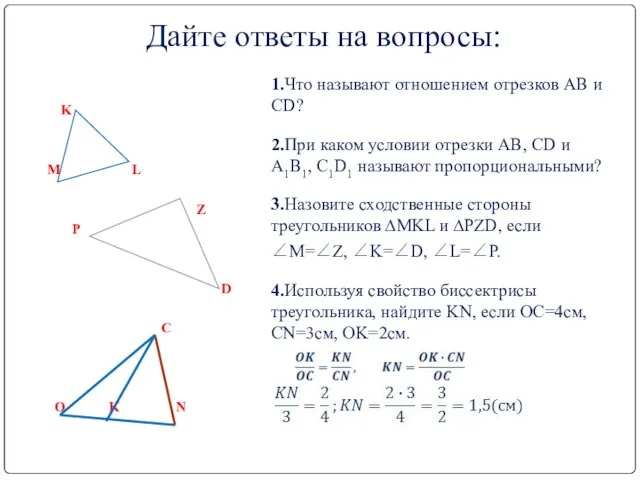
- 2. Дайте ответы на вопросы: 1.Что называют отношением отрезков AB и CD? 2.При каком условии отрезки AB,
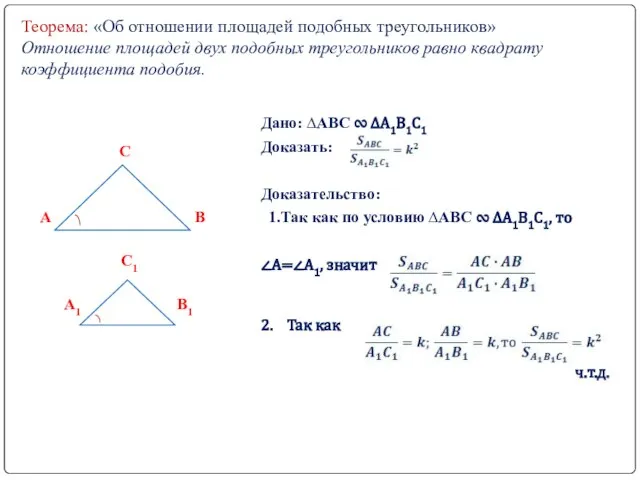
- 3. Теорема: «Об отношении площадей подобных треугольников» Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия. Дано:
- 4. Закрепление. № 544 Дано: ∆ABC ∾ ∆A1B1C1, Найти: AC Решение: 1.Так как по условию то по
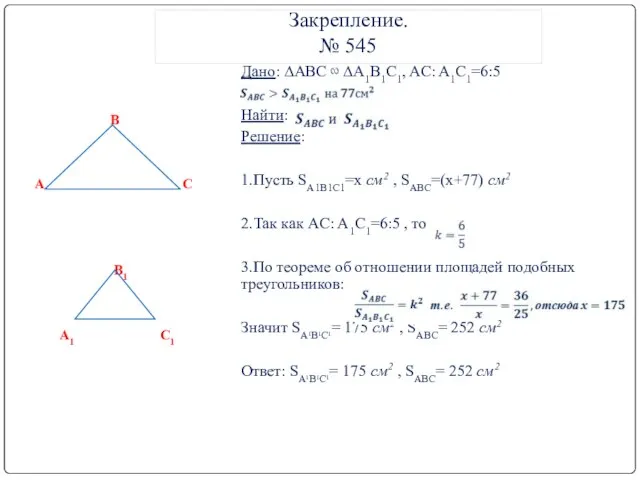
- 5. Закрепление. № 545 Дано: ∆ABC ∾ ∆A1B1C1, AC: A1C1=6:5 Найти: Решение: 1.Пусть SA1B1C1=x см2 , SABC=(x+77)
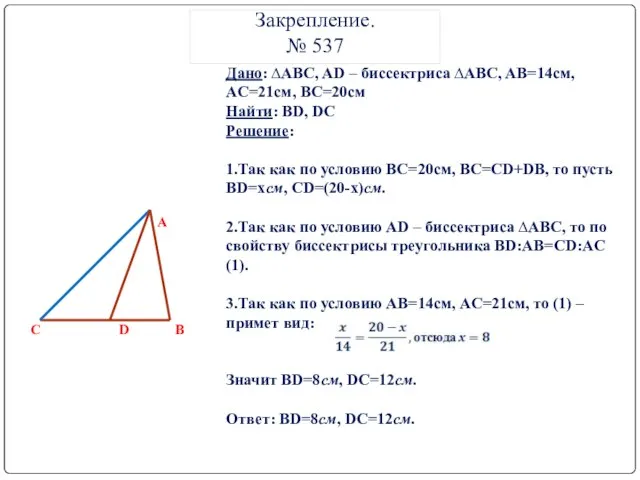
- 6. Закрепление. № 537 Дано: ∆ABC, AD – биссектриса ∆ABC, AB=14см, AC=21см, BC=20см Найти: BD, DC Решение:
- 7. Домашнее задание: Глава VII, § 1, п56-п58; вопросы 1-4 (стр 160); № 538 – «3» №
- 8. Самопроверка домашнего задания по образцу № 538 Дано: ∆ABC, AD – биссектриса ∆ABC, CD=4,5см, BD=13,5см, PABC=42см.
- 9. Самопроверка домашнего задания по образцу № 547 Дано: ∆ABC ∾ ∆A1B1C1 Доказать: Доказательство: 1.Так как по
- 11. Скачать презентацию




 Дискретная математика. Основные понятия и определения графа и его элементов
Дискретная математика. Основные понятия и определения графа и его элементов Старинный способ решения задач на смеси и сплавы
Старинный способ решения задач на смеси и сплавы Поняття та призначення функцій
Поняття та призначення функцій Математика
Математика Векторное исчисление
Векторное исчисление История возникновения геометрии как науки
История возникновения геометрии как науки Смежные и вертикальные углы. Решение задач
Смежные и вертикальные углы. Решение задач Формулы сокращенного умножения
Формулы сокращенного умножения Описание линейной дискретной системы в частотной области (ЛДС). Частотные характеристики ЛДС
Описание линейной дискретной системы в частотной области (ЛДС). Частотные характеристики ЛДС Единицы времени. Час. минута
Единицы времени. Час. минута Презентация на тему Дифференцирование частного и степени
Презентация на тему Дифференцирование частного и степени  Простейшие векторные операции и их реализация на языке MATLAB
Простейшие векторные операции и их реализация на языке MATLAB Теория вероятности в жизни пчел
Теория вероятности в жизни пчел Теорема Пифагора
Теорема Пифагора Задачи на проценты. ОГЭ
Задачи на проценты. ОГЭ Презентация на тему Осевая симметрия
Презентация на тему Осевая симметрия  Прибавить и вычесть 3. Решение текстовых задач. Урок №57
Прибавить и вычесть 3. Решение текстовых задач. Урок №57 Презентация на тему Иррациональные уравнения
Презентация на тему Иррациональные уравнения 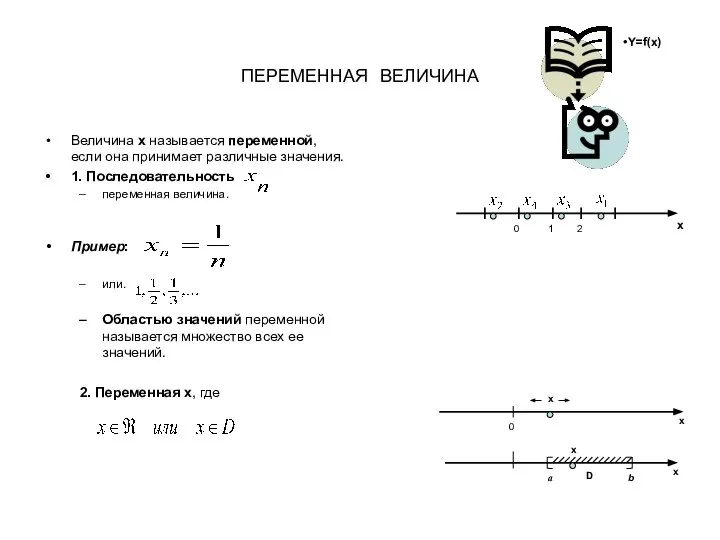 Понятие функции, предел
Понятие функции, предел Иррациональные уравнения
Иррациональные уравнения Путешествие в страну математики. Дидактическая игра Веселые цифры
Путешествие в страну математики. Дидактическая игра Веселые цифры Презентация на тему График квадратичной функции. Неравенства с одной переменной
Презентация на тему График квадратичной функции. Неравенства с одной переменной  Тема урока: «Аксиомы стереометрии и их следствия. Решение задач»
Тема урока: «Аксиомы стереометрии и их следствия. Решение задач» Прямоугольник, ромб, квадрат
Прямоугольник, ромб, квадрат Умножение числа на произведение
Умножение числа на произведение Графическое решение уравнений
Графическое решение уравнений Морской бой
Морской бой Круглые числа
Круглые числа