Свойства функций

Линейная функция.
1.D (f) = (- ∞;∞)
2.E (f) = ( - ∞;∞)
3.f (x) = 0 ,при x= -0.5
4.f (x) > 0, если x > -0,5
5.f (x) < 0, если x < -0,5
6.f (x) возрастает на всей области определения
8.f (x)наиб. не сущ.
9.f (x)наим. не сущ.
10.Функция не является ни четной, ни нечетной.
Пергамент знаний.
Ссылка на источник.
У
Х
Пример:
f (x)= 2x + 1
а) Графиком функции является прямая,
б)График функции проходит через точки (-0,5;0) и (0;1)
-0.5
1
II
I
III
IV

Прямая пропорциональность.
Пример:
f (x) = kx, k>0
а)Графиком функции является прямая;
б)График функции проходит через точку (0;0)
в)График функции расположен в I и III координатных четвертях.
1.D (f) = (- ∞; ∞)
2.Е (f) = ( - ∞; ∞)
3.f (x) = 0, при х = 0
4.f (x) > 0, при x > 0
5.f (x) < 0, при x < 0
6.f (x) возрастает в промежутке
(- ∞; ∞), т.е. на всей числовой прямой.
7.f (x)наиб.- не сущ.
8.f (x)наим.- не сущ.
9.f (-x) = - f (x)
Функция является нечетной.
Пергамент знаний.
Ссылка на источник.
III
IV
II
I
У
Х

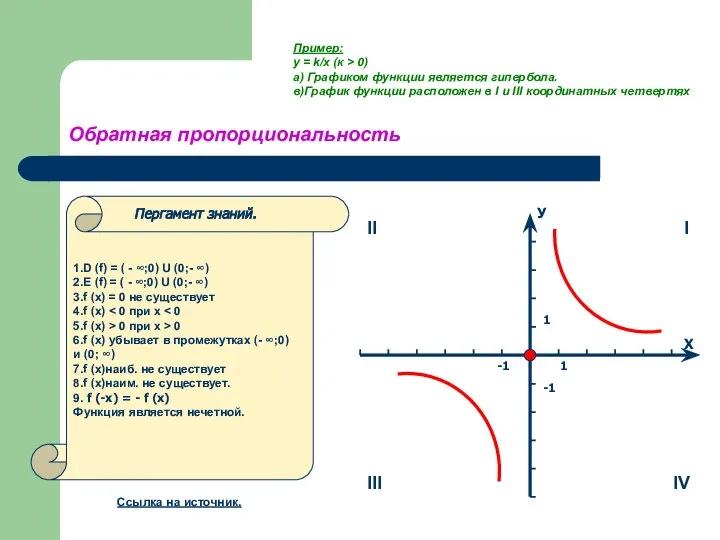
Обратная пропорциональность
1.D (f) = ( - ∞;0) U (0;- ∞)
2.E (f) = ( - ∞;0) U (0;- ∞)
3.f (x) = 0 не существует
4.f (x) < 0 при х < 0
5.f (x) > 0 при x > 0
6.f (x) убывает в промежутках (- ∞;0)
и (0; ∞)
7.f (x)наиб. не существует
8.f (x)наим. не существует.
9. f (-x) = - f (x)
Функция является нечетной.
Пергамент знаний.
Ссылка на источник.
Пример:
y = k/x (к > 0)
а) Графиком функции является гипербола.
в)График функции расположен в I и III координатных четвертях
У
Х
II
III
I
IV
1
-1
1
-1

Пример построения графика линейной функции
y
x
1
2
0
5
Пример: y=2x+1
Если x=0, то y=2 • 0+1=1
Если x=2, то y=2•2+1=5

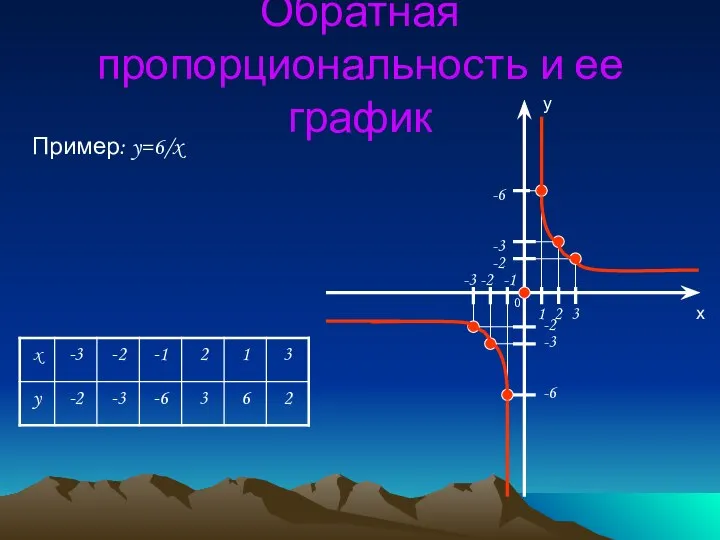
Обратная пропорциональность и ее график
Пример: y=6/x
-2
-3
-6
-1
-2
-3
-6
-2
-3
1
2
3
y
x
0