Содержание
- 2. 2.1. Маршруты, цепи, циклы
- 3. Маршруты
- 4. Цепи и циклы
- 5. Лемма. Всякий маршрут графа содержит хотя бы одну простую цепь, соединяющую ту же пару вершин. Доказательство
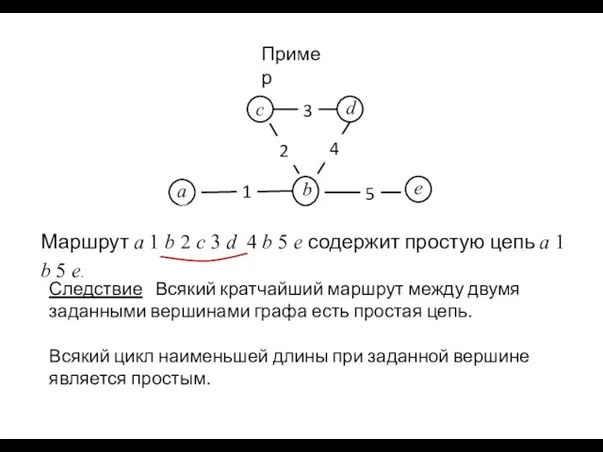
- 6. Пример Маршрут a 1 b 2 c 3 d 4 b 5 e содержит простую цепь
- 7. Если маршрут рассматривать с учетом ориентации ребер (может быть и по звеньям), то получим соответствующие определения:
- 8. Задачи о маршрутах В теории рассматривается ряд задач и алгоритмов определения свойств маршрутов: существование маршрутов заданной
- 9. Существование маршрутов Рассматривается неориентированный (маршрут не предполагает ориентации) униграф (важен лишь факт смежности вершин). Такой граф
- 10. и вершины xk и xj смежны. Для маршрутов других видов задаются соответствующие матрицы смежности.
- 11. Нахождение маршрутов Длина 1 a1a a2b b2a b3c b4c c3b c4b Длина 2 a1a1a a1a2b a2b2a
- 12. Число маршрутов
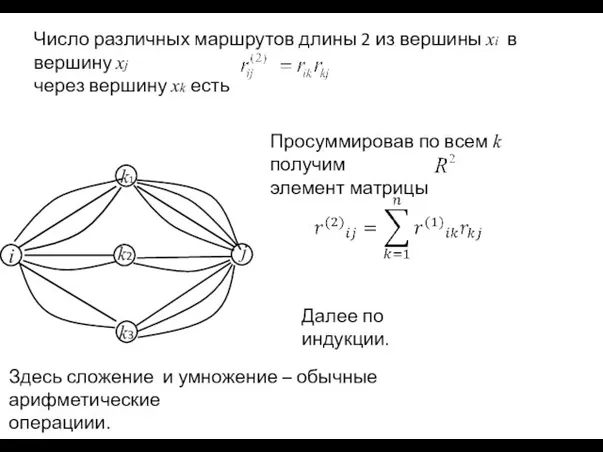
- 13. Число различных маршрутов длины 2 из вершины xi в вершину xj через вершину xk есть Далее
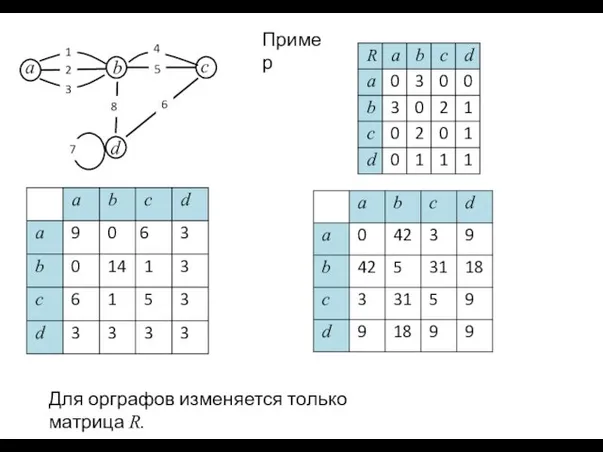
- 14. Пример Для орграфов изменяется только матрица R.
- 15. c
- 16. Достижимость
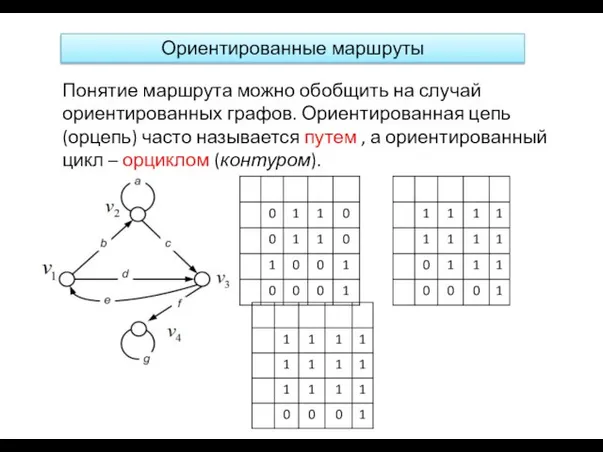
- 17. Ориентированные маршруты Понятие маршрута можно обобщить на случай ориентированных графов. Ориентированная цепь (орцепь) часто называется путем
- 18. 2.2. Компоненты связности
- 19. Компоненты и бикомпоненты
- 20. Отношение «быть в одной компоненте » для ребер – эквивалентность, как и для вершин.
- 21. Для ориентированных графов
- 22. Граф называется сильно связным, если он состоит из единственной бикомпоненты. Множество вершин, достижимых из вершины x,
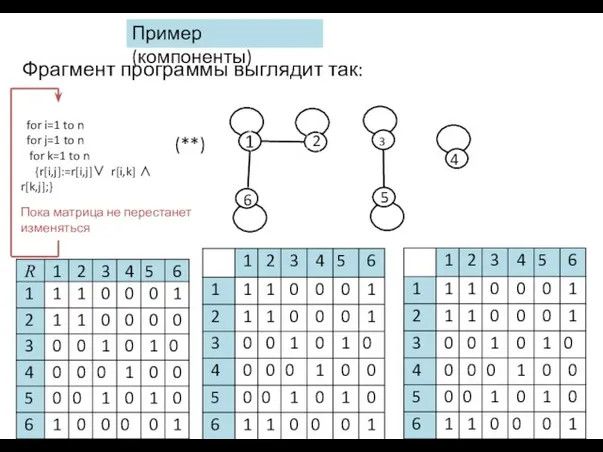
- 26. Фрагмент программы выглядит так: Пример (компоненты) 1 2 3 4 5 6 (**)
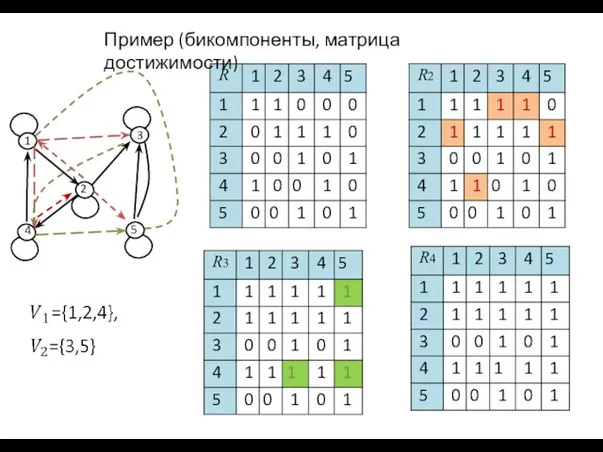
- 28. Пример (бикомпоненты, матрица достижимости) 1 2 3 5 4
- 29. Фрагмент программы: for k=1 to n for i=1 to n (***) for j=1 to n {r[i,j]:=r[i,j]∨r[i,k]
- 30. Ахо А., Хопкрофт Д., Ульман Д. (стр. 194-195) Структуры данных и алгоритмы. : Пер. с англ.
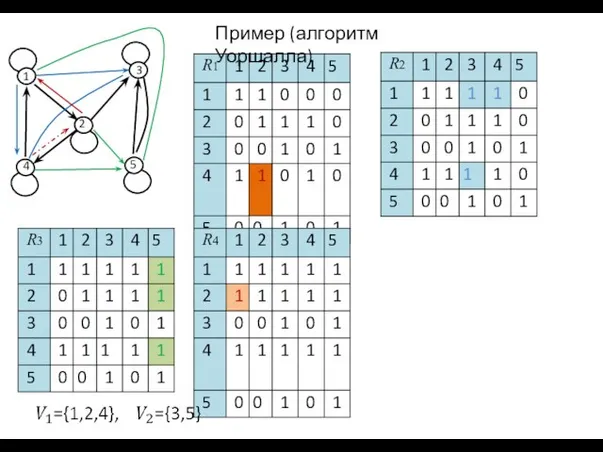
- 31. Пример (алгоритм Уоршалла)
- 32. Warshall Stephen (1935 – 2006) https://en.wikipedia.org/wiki/Stephen_Warshall Warshall carried out research and development in operating systems, compiler
- 33. 2.3. Кратчайшие цепи
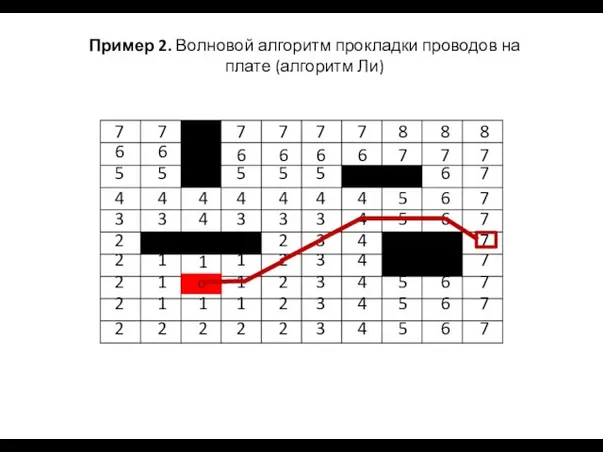
- 34. Волновой алгоритм
- 36. 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2
- 37. Взвешенный граф
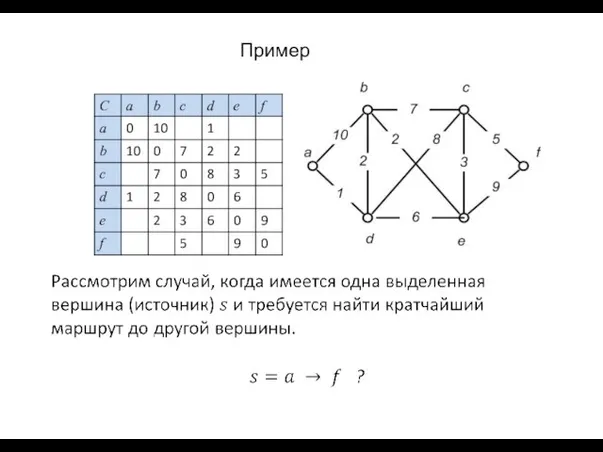
- 38. Пример
- 39. Алгоритм Беллмана - Форда
- 42. +
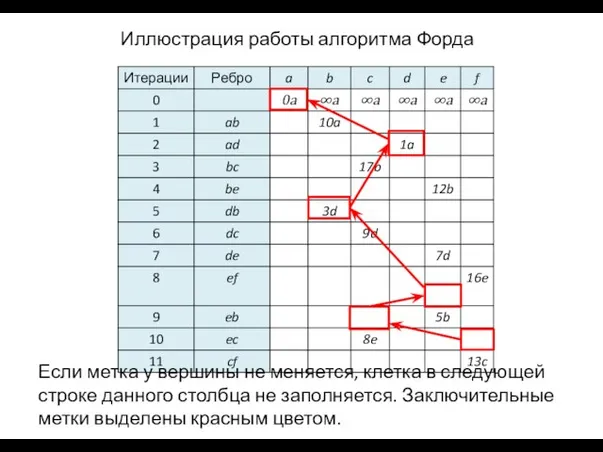
- 43. 0a ∞a ∞a 10 a ∞a ∞a ∞a 1 a 17b 12b 3 d 9 d
- 44. Если метка у вершины не меняется, клетка в следующей строке данного столбца не заполняется. Заключительные метки
- 45. В таком представлении алгоритм Беллмана — Форда более пригоден для «ручного» исполнения. Пусть вершины пронумерованы V={1,2,…,n}
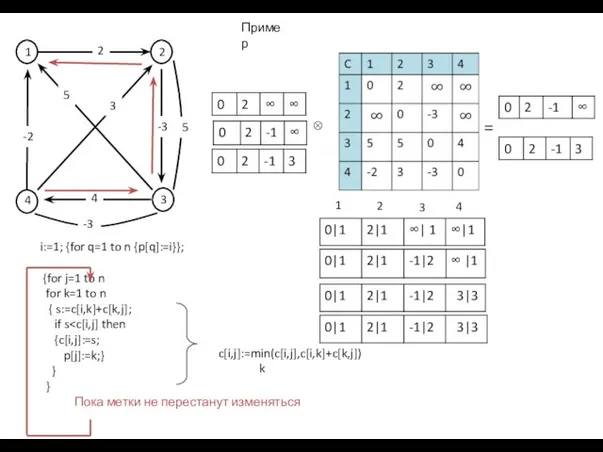
- 46. Пример 1 2 3 4 ⊗ =
- 47. БЕЛЛМАН, Ричард (1920- 1984) – «отец «динамического программирования» - американский математик. Опубликовал 619 статей и 39
- 48. Алгоритм Дейкстры
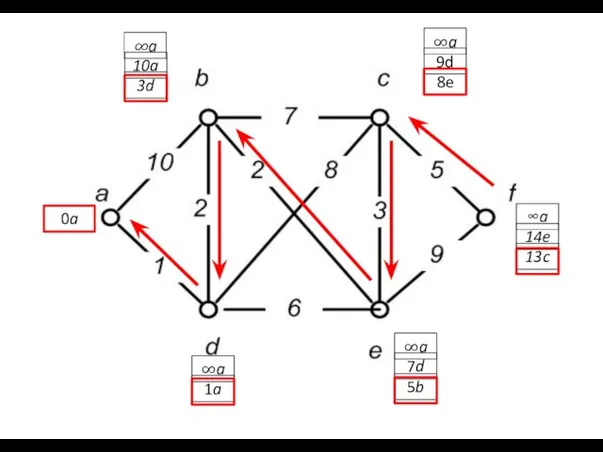
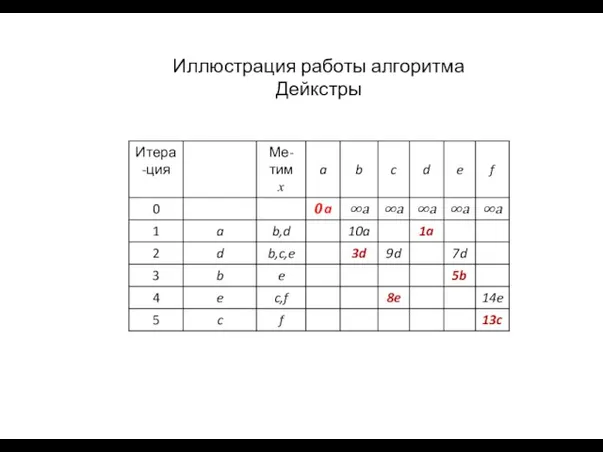
- 51. 0a ∞a ∞a ∞a ∞a ∞a 10a 1a 3d 9d 7d 5b 8e 14e 13c
- 52. Иллюстрация работы алгоритма Дейкстры
- 53. в
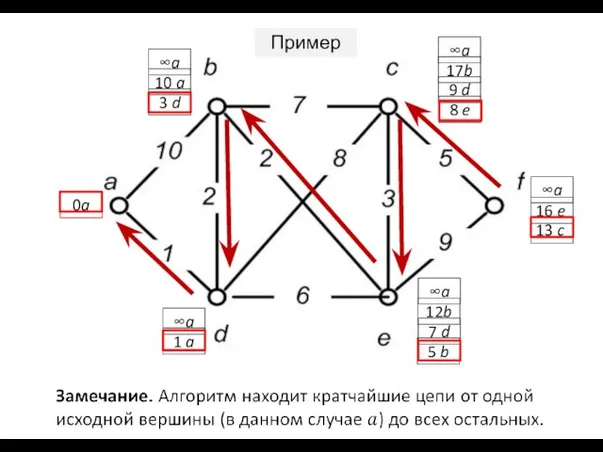
- 54. Обобщения 1. Алгоритмы Беллмана – Форда и Дейкстры легко распространяются на случай ориентированных (частично ориентированных) графов,
- 55. ДЕЙКСТРА, Эдсгер (Edsger Dijkstra, 1930-2002). Нидерландский учёный, труды которого оказали большое влияние на развитие информатики; один
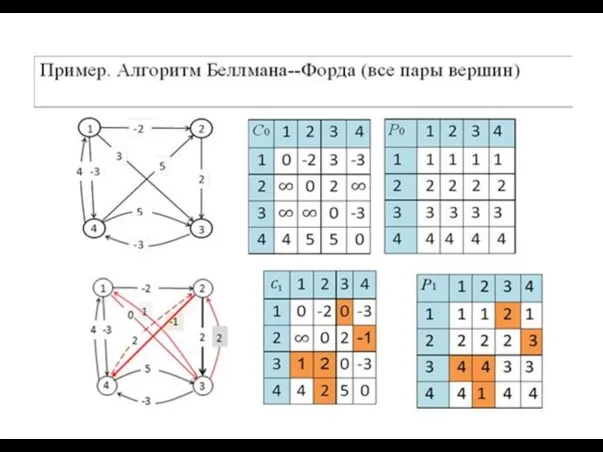
- 56. Алгоритм Беллмана--Форда 2 (все пары вершин)
- 57. А. Шимбел предложил такую операцию умножения матриц: суммирование заменяется на min, умножение на арифметическое сложение
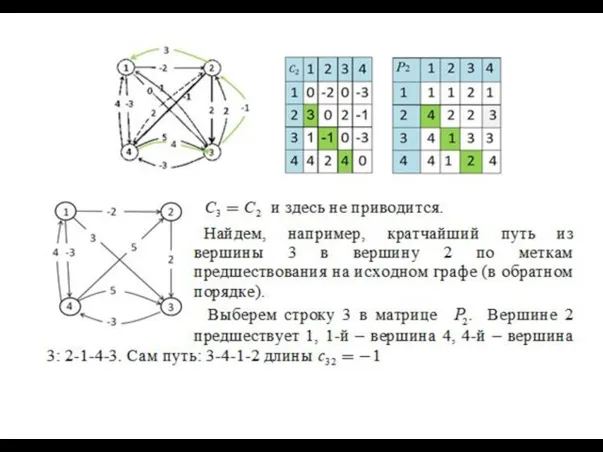
- 66. Элемент, например, матрицы будет Это означает, что при при просмотре троек вершин с нашлась такая вершина
- 67. Алгоритм Флойда Замечание. В алгоритме Флойда, так же как и в алгоритме Беллмана – Форда, нет
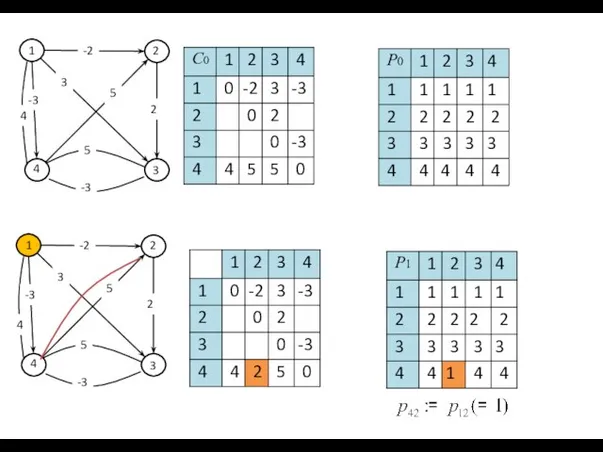
- 68. for i=1 to n for j=1 to n p[i,j]:=i; Инициализация Основной цикл Алгоритм работает «на месте»:
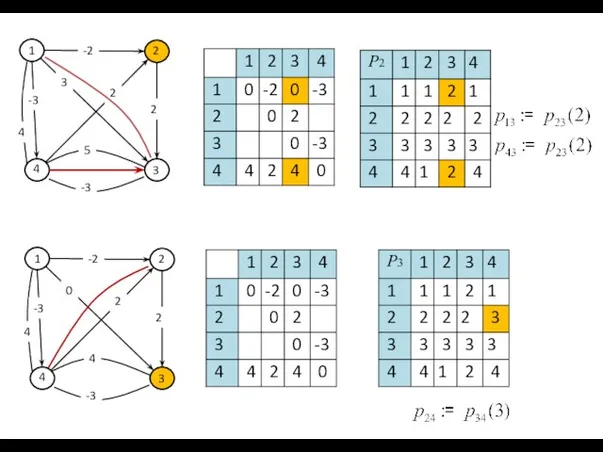
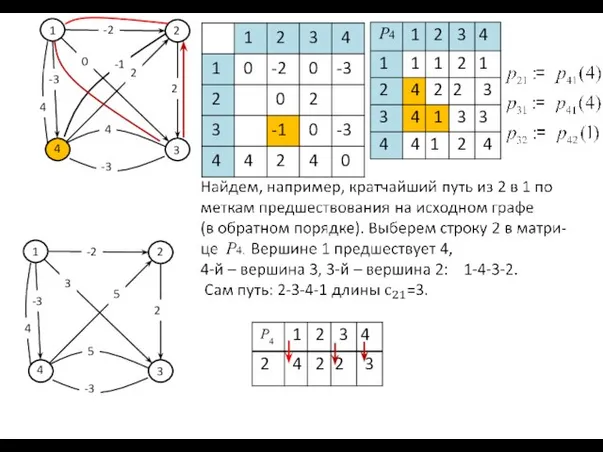
- 69. Фрагмент программы: for k=1 to n for i=1 to n for j=1 to n { s:=c[i,k]+c[k,j];
- 70. 4 4
- 71. 4 4
- 72. -1 4 4
- 73. Замечание. Алгоритмы Беллмана – Форда и Флойда работают кор- ректно, если в графе нет циклов отрицательной
- 75. ФЛОЙД, Роберт В (Robert W Floyd, 1936 – 2001) — американский учёный в области теории вычислительных
- 77. Скачать презентацию

















































![for i=1 to n for j=1 to n p[i,j]:=i; Инициализация Основной цикл](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/878733/slide-67.jpg)




 Коллинеарные векторы
Коллинеарные векторы Линейные неравенства
Линейные неравенства Правила дифференцирования
Правила дифференцирования Графики тригонометрических функций. 10 класс
Графики тригонометрических функций. 10 класс Логарифмические неравенства
Логарифмические неравенства Параллелепипед. Куб
Параллелепипед. Куб Симметрия в пространстве
Симметрия в пространстве Знакомьтесь, открытые задачи. Мастер-класс
Знакомьтесь, открытые задачи. Мастер-класс Случаи вычитания 12 -
Случаи вычитания 12 - Введение декартовых координат в пространстве. Формулы середины отрезка и расстояния между двумя точками
Введение декартовых координат в пространстве. Формулы середины отрезка и расстояния между двумя точками Измерение углов поворота в радианах. Алгебра 9 класс
Измерение углов поворота в радианах. Алгебра 9 класс Основы алгебры логики
Основы алгебры логики Деление
Деление Презентация на тему Прикладные задачи на экстремумы
Презентация на тему Прикладные задачи на экстремумы  Презентация на тему Квадратные уравнения. Основные свойства
Презентация на тему Квадратные уравнения. Основные свойства  Тригонометрические уравнения. Устный счет
Тригонометрические уравнения. Устный счет Сложение и вычитание чисел с переходом через десяток
Сложение и вычитание чисел с переходом через десяток Построение и анализ графиков в среде Живая геометрия. 9 класс
Построение и анализ графиков в среде Живая геометрия. 9 класс Умножение обыкновенных дробей
Умножение обыкновенных дробей Презентация на тему АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ ПРОИЗВОЛЬНЫХ СТЕПЕНЕЙ
Презентация на тему АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ ПРОИЗВОЛЬНЫХ СТЕПЕНЕЙ  Свойства сложения и умножения - Презентация_
Свойства сложения и умножения - Презентация_ Линии и углы в окружности
Линии и углы в окружности Презентация_к_уроку_Сложение_и_вычитание_алгебраических_дробей_с
Презентация_к_уроку_Сложение_и_вычитание_алгебраических_дробей_с Формулы преобразования суммы и разности тригонометрических функций в произведение
Формулы преобразования суммы и разности тригонометрических функций в произведение Индивидуальное задание №8. Построение линии пересечения тора и конуса
Индивидуальное задание №8. Построение линии пересечения тора и конуса Задачи на построение
Задачи на построение Геометрия с Дракошей (2 класс)
Геометрия с Дракошей (2 класс) Таблица умножение числа 5
Таблица умножение числа 5