Слайд 2Задача.
Построить треугольник по данной стороне, углу, к ней прилежащему, и сумме двух

других его сторон.
Слайд 3
Цель:
1) Получить более полное представление о методе спрямления;
2) Изучить применение метода

в решении различных задач на построение.
Основные задачи:
1) Проанализировать литературу по данной теме;
2) Выделить опорные задачи в зависимости от условий;
3) Научиться использовать их при решении более сложных задач.
Слайд 4
Гипотеза.
Существуют ли опорные задачи рассматриваемого метода.
Методы работы.
Поисковый метод;
Метод декомпозиции;
Работа

с дополнительной литературой.
Слайд 5Метод спрямления состоит в том, что некоторую ломаную линию в чертеже заменяют

прямой. После решения новой задачи определяют, в какой точке надо согнуть выпрямленную прямую и таким образом перейти к первоначальной задаче. Особенно этот метод применим в тех задачах, условия которых содержат данную сумму или разность частей некоторой ломаной.
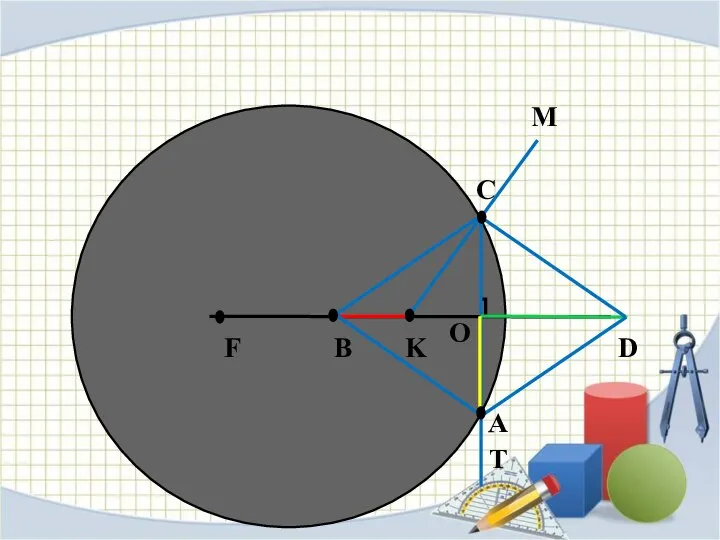
Слайд 6ЗАДАЧА №1
Построить треугольник по данной стороне, углу, к ней прилежащему, и
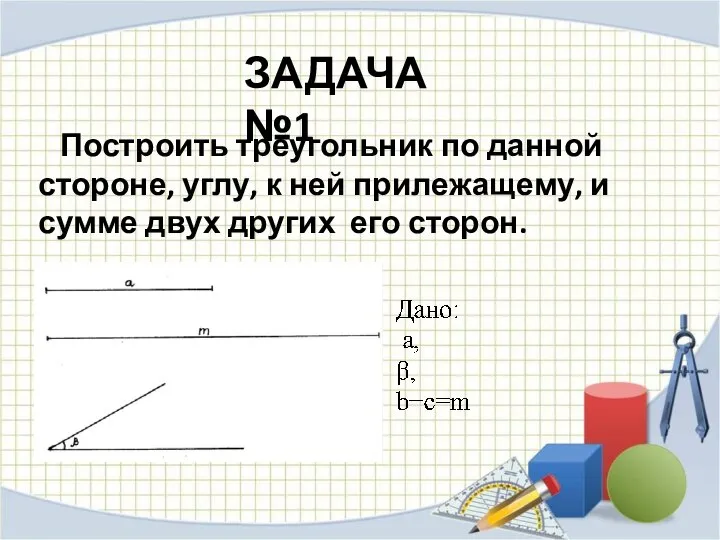
сумме двух других его сторон.
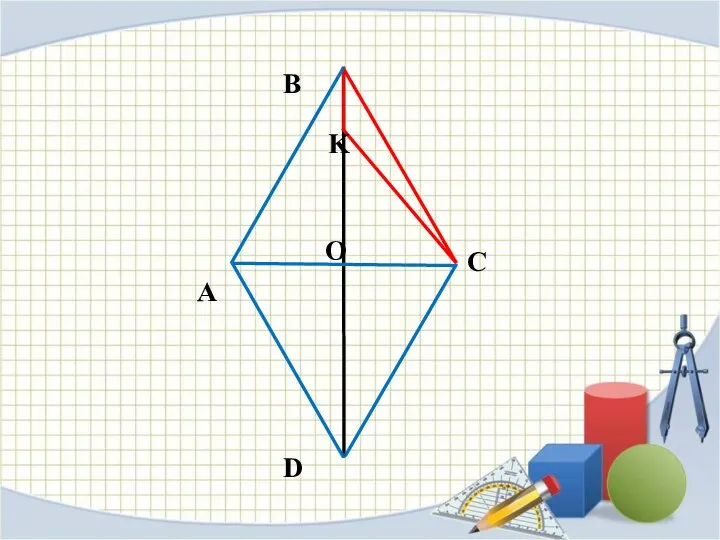
Слайд 10ЗАДАЧА №2
Построить ромб по разности диагоналей и стороне.
Дано:
а
m

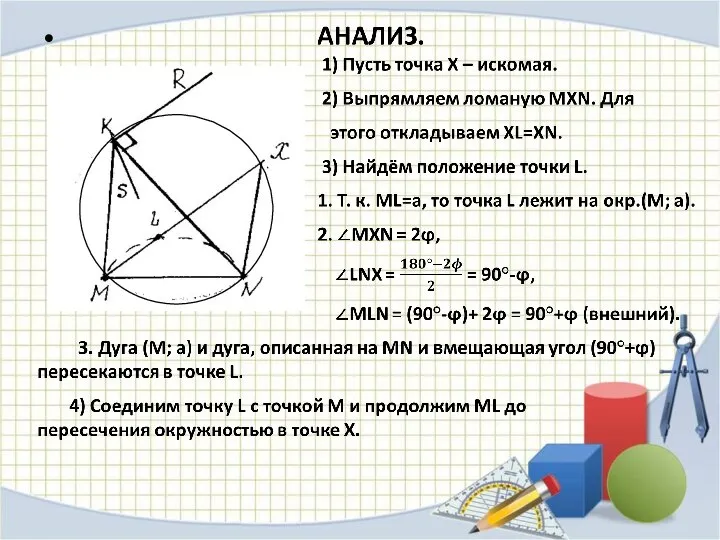
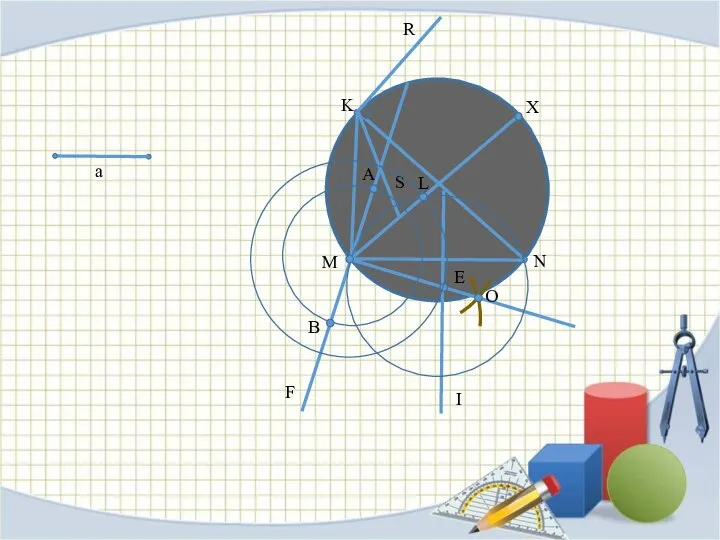
Слайд 13 ЗАДАЧА №3.
Дана окружность и на ней точки M и N. Найти
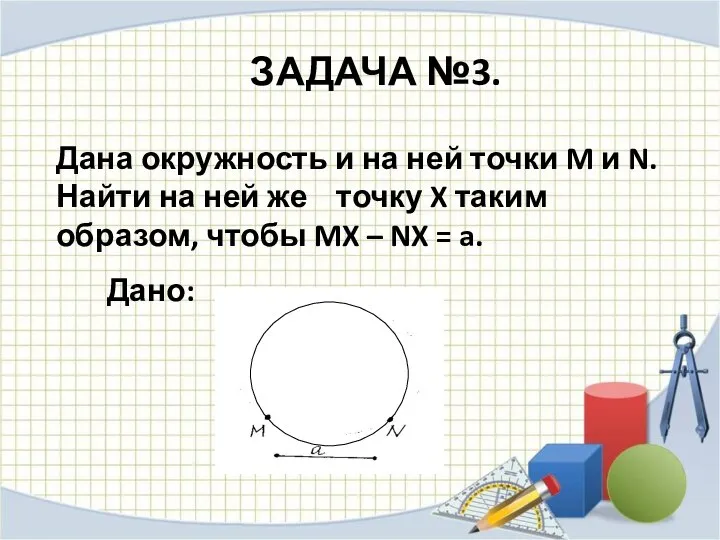
на ней же точку X таким образом, чтобы MX – NX = a.
Дано:
Слайд 16
Заключение
Работая над представленной темой, мы:
исследовали решения различных задач;
проанализировали литературу по данному вопросу

и обобщили полученные результаты;
убедились, что выдвинутая нами гипотеза подтверждается – существуют опорные задачи для треугольников и четырехугольников;
смогли применить полученные знания на уроках черчения и поделились опытом со своими одноклассниками на уроках геометрии по теме «Решение задач на построение».









 Знакомство с линиями чертежа Замкнутая, незамкнутая
Знакомство с линиями чертежа Замкнутая, незамкнутая Презентация по математике "Решение задач с помощью систем уравнений второй степени" -
Презентация по математике "Решение задач с помощью систем уравнений второй степени" -  Площадь прямоугольника
Площадь прямоугольника Геометрическая прогрессия
Геометрическая прогрессия Производная функции
Производная функции Числоа 6, 7. Письмо цифры 6
Числоа 6, 7. Письмо цифры 6 Измерительные работы
Измерительные работы Своя игра 1
Своя игра 1 Решение уравнений и неравенств заданий С3
Решение уравнений и неравенств заданий С3 Неопределенный интеграл
Неопределенный интеграл Пустое множество
Пустое множество Методы отбора единиц наблюдения для выборочной совокупности. Возможные типы систематических ошибок оценки в исследованиях
Методы отбора единиц наблюдения для выборочной совокупности. Возможные типы систематических ошибок оценки в исследованиях Подготовка к ПА
Подготовка к ПА Асимптотические методы. Граничные условия на горизонтальной скважине. (Лекция 3)
Асимптотические методы. Граничные условия на горизонтальной скважине. (Лекция 3) Математический диктант
Математический диктант Математическая статистика
Математическая статистика Математический турнир Степень и ее свойства. 7 класс
Математический турнир Степень и ее свойства. 7 класс Тригонометрические функции
Тригонометрические функции Деление десятичной дроби на натуральное число
Деление десятичной дроби на натуральное число Прибавление числа 6 с переходом через десяток
Прибавление числа 6 с переходом через десяток Дифференциальное исчисление функций нескольких переменных
Дифференциальное исчисление функций нескольких переменных Линейное уравнение с двумя переменными
Линейное уравнение с двумя переменными krivye-vtorogo-poryadka (1)
krivye-vtorogo-poryadka (1) Геометрический и физический смысл производной. Решение задач
Геометрический и физический смысл производной. Решение задач Основное свойство дроби
Основное свойство дроби Информационная безопасность. Базовые логические элементы, применяемые в вычислительной технике
Информационная безопасность. Базовые логические элементы, применяемые в вычислительной технике Круги Эйлера в решении задач
Круги Эйлера в решении задач Учимся писать цифры
Учимся писать цифры