Технология подготовки учащихся к овладению функциональными методами решения задач с параметрами. Занятие №2
Содержание
- 2. Содержание курса 2
- 3. Содержание О функциональном методе решения задач с параметрами ЕГЭ 2014-2015 (было и предлагают в материалам методических
- 4. О функциональном методе решения задач с параметрами Функциональный метод решения задач с параметрами является составной частью
- 5. ЕГЭ 2010-2014 (функциональный метод, задачи)
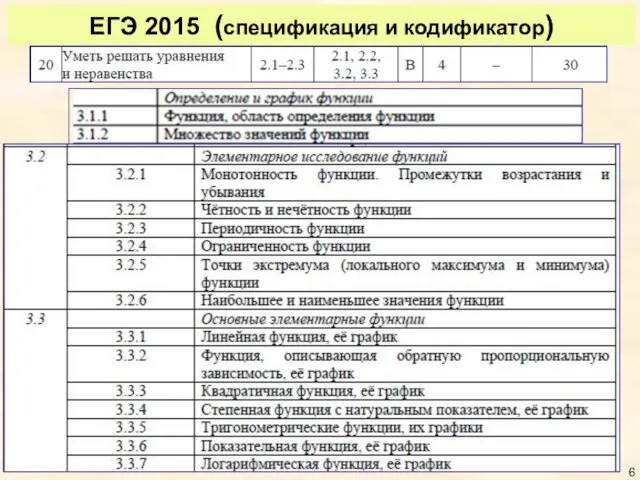
- 6. ЕГЭ 2015 (спецификация и кодификатор)
- 7. Литература для подготовки по заданию 20 ЕГЭ 2015 профильного уровней
- 8. Литература для подготовки по заданию 20 ЕГЭ 2015 профильного уровней
- 9. Функциональные методы решения в электронных пособиях Прокофьева А.А. и Корянова А.Г. Адреса: http://alexlarin.net/ege/2012/C5-2012.http://alexlarin.net/ege/2012/C5-2012. html и http://www.alexlarin.net/ege/2011/c52011.html
- 10. Классификация задач, решаемых функциональными методами
- 11. С чего следует начать? Начать следует с повторения свойств функций (пункт 3.2 кодификатора к ЕГЭ 2015)
- 12. Область определения функции Для решения задач этого типа следует знать и помнить области определения всех элементарных
- 13. Область определения функции (задачи)
- 14. Область определения функции (ответы)
- 15. Область значений функции Знание области значений функции оказывается полезным при решении уравнений и неравенств в следующих
- 16. Область значений функции Полезно знать и уметь находить область значений функций на все области определения и
- 17. Область значений функции Полезно знать и уметь находить область значений функций на все области определения и
- 18. Область значений функции Статья. Прокофьев А.А., Бардушкин В.В. Использование свойств функции при решении задач. «Математика в
- 20. Область значений функции
- 21. Область значений функции (задачи и ответы) Ответы:
- 22. Четность, нечетность функции
- 23. Четность, нечетность функции
- 24. Четность, нечетность функции
- 25. Четность, нечетность функции
- 26. Четность, нечетность функции (задачи)
- 27. Четность, нечетность функции (ответы)
- 28. Четность, нечетность функции Статья: Прокофьев А.А. Использование свойств симметрии выражений относительно переменных при решении задач. «Математика
- 29. Непрерывность функции (задачи и ответы) Ответы.
- 30. Использование обратной функции
- 31. Использование обратной функции
- 32. Использование обратной функции (задачи)
- 33. Использование обратной функции (ответы)
- 34. Использование ограниченности функции Метод оценки (минимаксные задачи) Идея метода минимаксов. Иначе говоря, уравнение можно переписать в
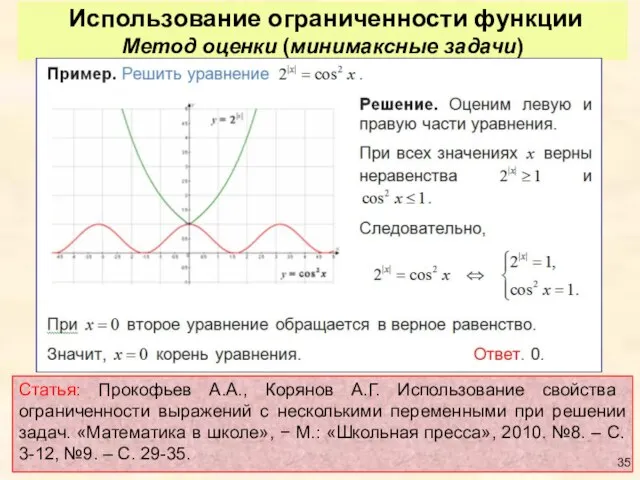
- 35. Использование ограниченности функции Метод оценки (минимаксные задачи) Статья: Прокофьев А.А., Корянов А.Г. Использование свойства ограниченности выражений
- 36. Использование ограниченности функции Метод оценки (минимаксные задачи)
- 37. Использование ограниченности функции Метод оценки (минимаксные задачи)
- 38. Использование ограниченности функции (использование неотрицательности функции) Найдите все пары действительных чисел a и b, при которых
- 39. Использование ограниченности функции (использование неотрицательности функции)
- 40. Использование ограниченности функции (наибольшее и наименьшее значения функции)
- 41. Наибольшее и наименьшее значения функции
- 42. В некоторых задачах для нахождения множества значений функции (нахождения наибольшего или наименьшего значений) удобно ввести параметр.
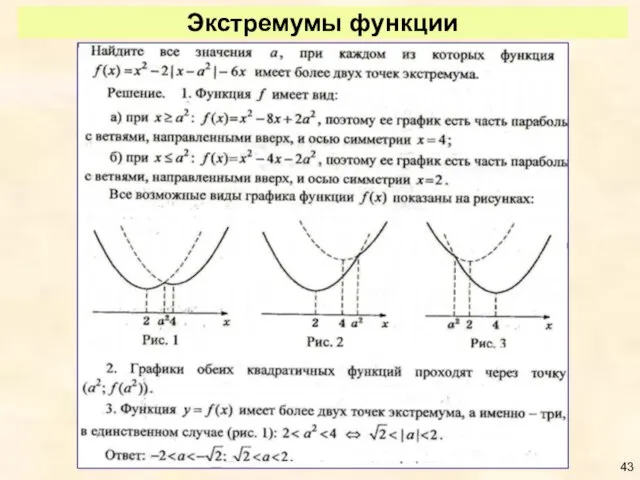
- 43. Экстремумы функции
- 44. Экстремумы функции
- 45. Наибольшие и наименьшие значения функции и экстремумы
- 46. Наибольшее и наименьшее значения функции (задачи)
- 47. Наибольшее и наименьшее значения функции (ответы)
- 48. Наибольшее и наименьшее значения функции (ответы)
- 49. Использование монотонности функции (монотонность функции на промежутке) Статья: Прокофьев А.А., Бардушкин В.В. и др. Композиция функций
- 50. Использование монотонности функции (монотонность функции на промежутке)
- 51. Использование монотонности функции (монотонность функции на множестве R)
- 52. Использование монотонности функции (монотонность функции на множестве R)
- 53. Монотонность функции (задачи)
- 54. Монотонность функции (ответы)
- 55. Монотонность функции (задачи и ответы)
- 56. Логарифмические уравнения и неравенства При решении логарифмических уравнений и неравенств используются следующие логические схемы, основанные на
- 57. Задание 20. Логарифмические уравнения
- 58. Логарифмические неравенства
- 59. Использование монотонности функции (функции разной монотонности)
- 60. Функции разной монотонности
- 61. Использование монотонности функции Задачи вида
- 62. Доказательство утверждения Задачи вида
- 63. Метод рационализации
- 64. Применение метода рационализации Сначала демонстрация применения метода для решения неравенства без параметра.
- 65. Применение метода рационализации
- 66. Периодические функции и параметр (задачи) Учебник. Шабунин М.И., Прокофьев А.А. Математика. Алгебра. Начала математического анализа. Профильный
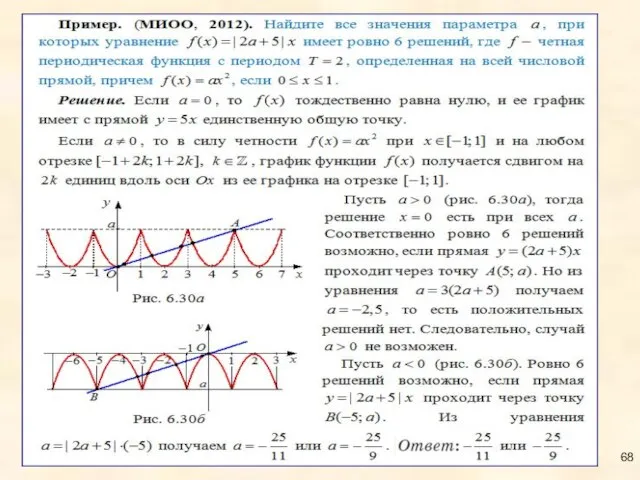
- 67. Периодические функции и параметр
- 69. Периодические функции и параметр (задачи)
- 70. Периодические функции и параметр (ответы)
- 71. Применение производной Статья: Прокофьев А.А., Корянов А.Г. Различные подходы к решению задач С5 ЕГЭ. «Математика», −
- 72. Применение производной
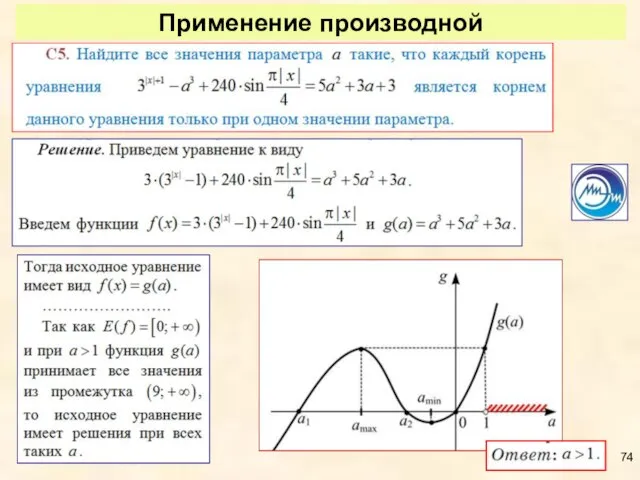
- 74. Применение производной
- 75. Печатные и электронные ресурсы Школьные учебники. Пособия для подготовки к ЕГЭ по математике. Журналы «Математика в
- 77. Скачать презентацию





































































 Векторы на плоскости
Векторы на плоскости Четырехугольники
Четырехугольники Векторы. Действия с векторами
Векторы. Действия с векторами Презентация на тему Число и цифра 3. Состав числа 3 (1 класс)
Презентация на тему Число и цифра 3. Состав числа 3 (1 класс)  Замечательные точки и линии треугольника. 9 класс
Замечательные точки и линии треугольника. 9 класс Занимательная математика
Занимательная математика Линейная алгебра
Линейная алгебра Монотонность функции
Монотонность функции Variācijas, permutācijas, kombinācijas
Variācijas, permutācijas, kombinācijas Математика на олимпийских играх. Керлинг. Разработка для учащихся 5 класса
Математика на олимпийских играх. Керлинг. Разработка для учащихся 5 класса Внутренний контроль качества результатов КХА
Внутренний контроль качества результатов КХА Треугольники. Часть 1
Треугольники. Часть 1 Дробные рациональные уравнения. Задания для интерактивной доски. 8 класс
Дробные рациональные уравнения. Задания для интерактивной доски. 8 класс Правильные многогранники
Правильные многогранники Презентация на тему Применение производной
Презентация на тему Применение производной  Элементы нелинейного функционального анализа. Гладкие многообразия. Два способа задания атласа на окружности
Элементы нелинейного функционального анализа. Гладкие многообразия. Два способа задания атласа на окружности Делаем математику видимой. Мяч из треугольников для квеста
Делаем математику видимой. Мяч из треугольников для квеста Матричная алгебра. Лекция 2
Матричная алгебра. Лекция 2 Задачи на нахождение расстояния между вершинами многогранника, все двугранные углы которого, прямые
Задачи на нахождение расстояния между вершинами многогранника, все двугранные углы которого, прямые 1-2_1
1-2_1 Треугольник. Подготовка к контрольной работе
Треугольник. Подготовка к контрольной работе Умножение для ленивых? 5 класс
Умножение для ленивых? 5 класс Плоская линия в R2
Плоская линия в R2 Действия с десятичными дробями. Интерактивный тренажёр
Действия с десятичными дробями. Интерактивный тренажёр Тест по теме функция
Тест по теме функция Применение комплексных чисел на практике
Применение комплексных чисел на практике Презентация на тему Уменьшаемое. Вычитаемое. Разность
Презентация на тему Уменьшаемое. Вычитаемое. Разность  Симметрия в искусстве
Симметрия в искусстве