Содержание
- 2. Теорема Пифагора
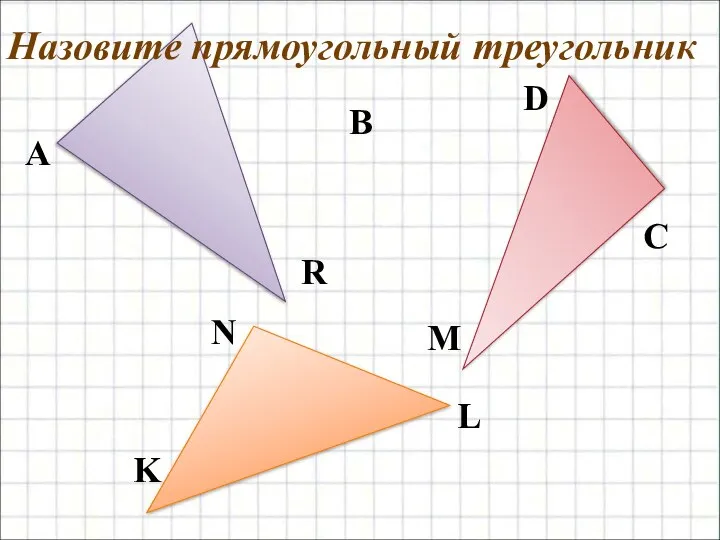
- 3. D C Назовите прямоугольный треугольник
- 4. A B C Свойства прямоугольного треугольника.
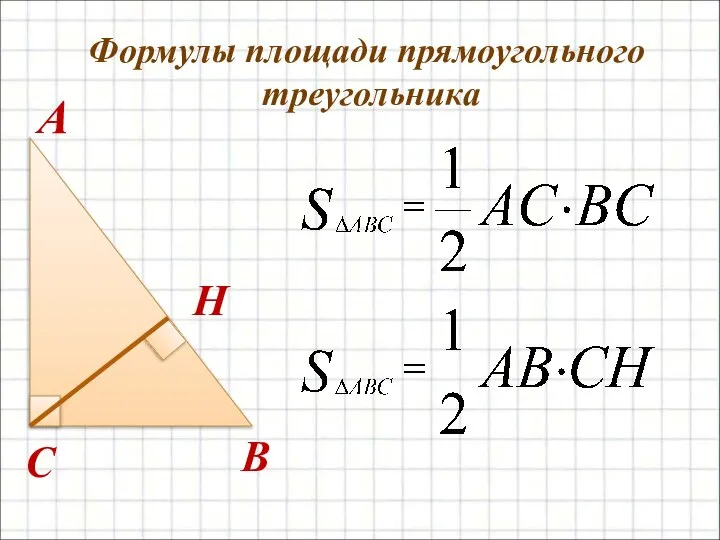
- 5. Формулы площади прямоугольного треугольника B C A H
- 6. Историческая справка Египетские строители и землемеры для определения прямого угла на плоскости использовали самую простую веревку
- 7. Историческая справка.
- 8. Задачи на чертежах
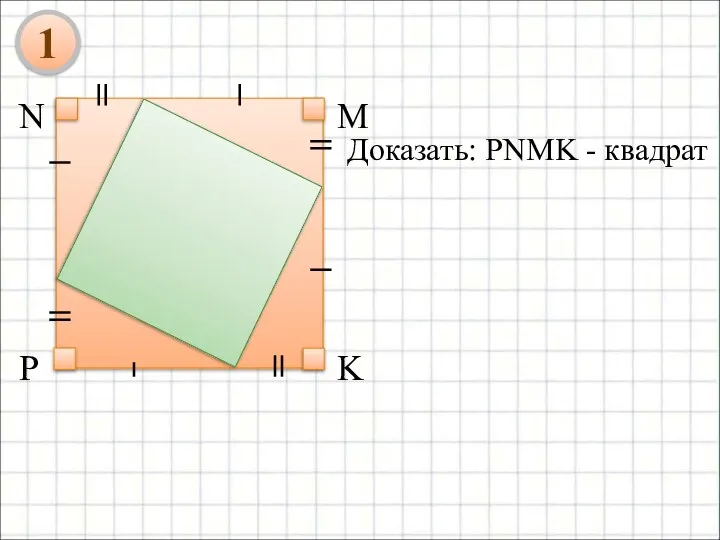
- 9. Доказать: PNMK - квадрат 1
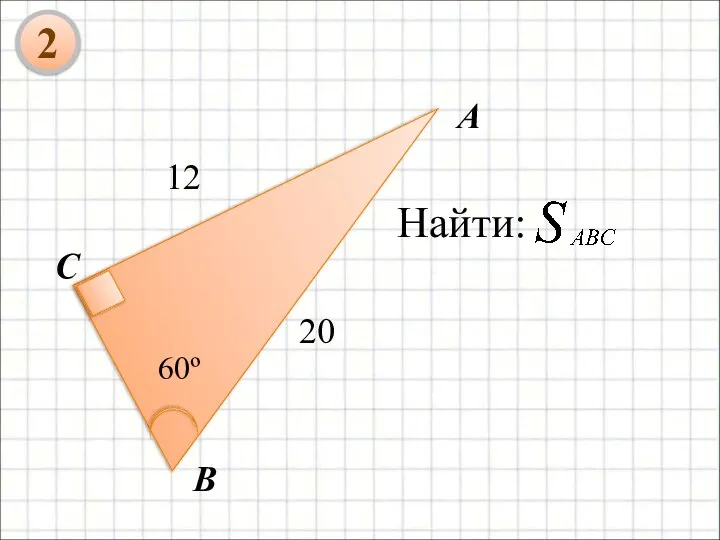
- 10. Найти: 2
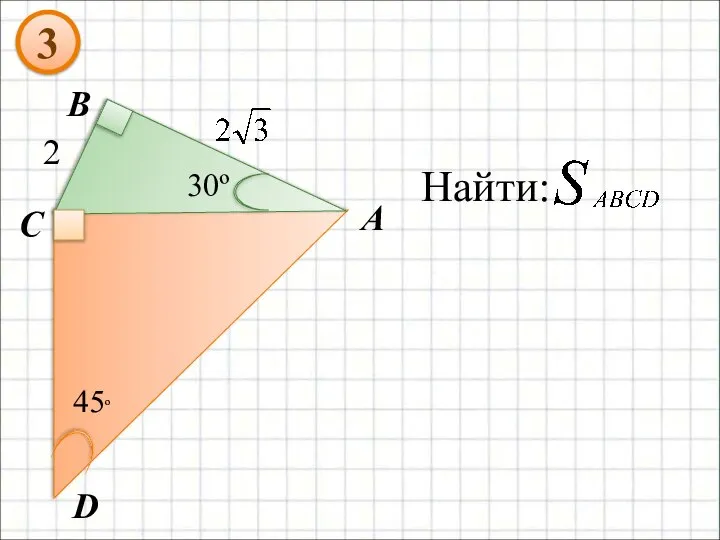
- 11. A B C 30º D 45º Найти: 2 3
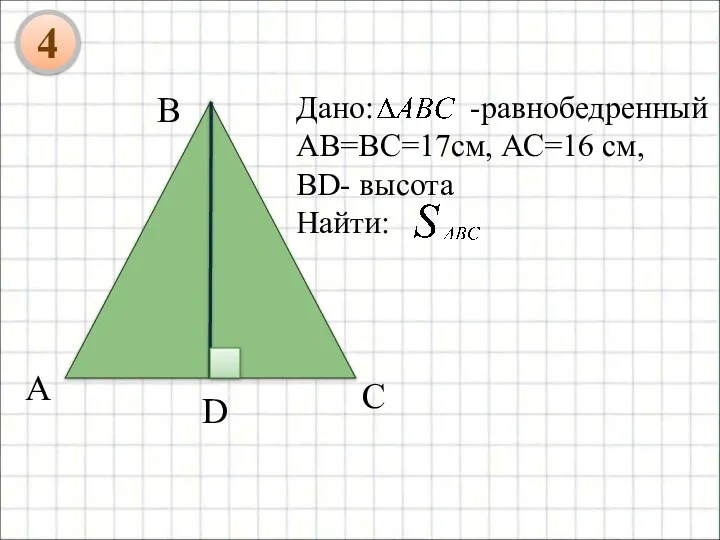
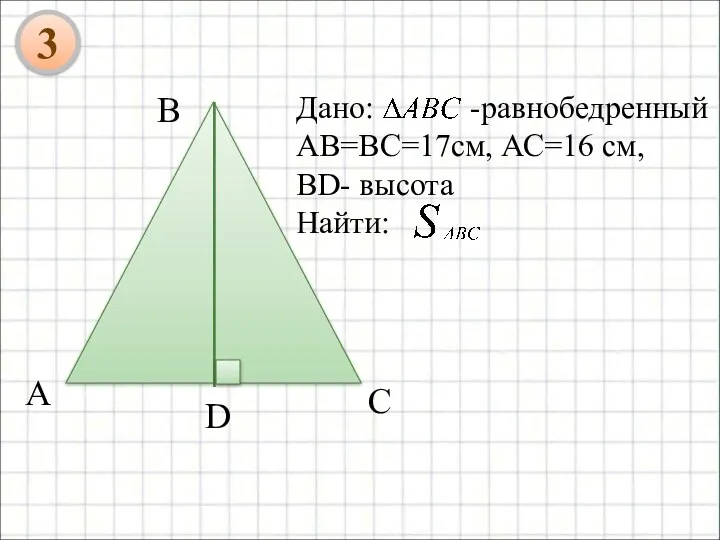
- 12. Дано: -равнобедренный AB=BC=17см, АС=16 см, BD- высота Найти: В 4
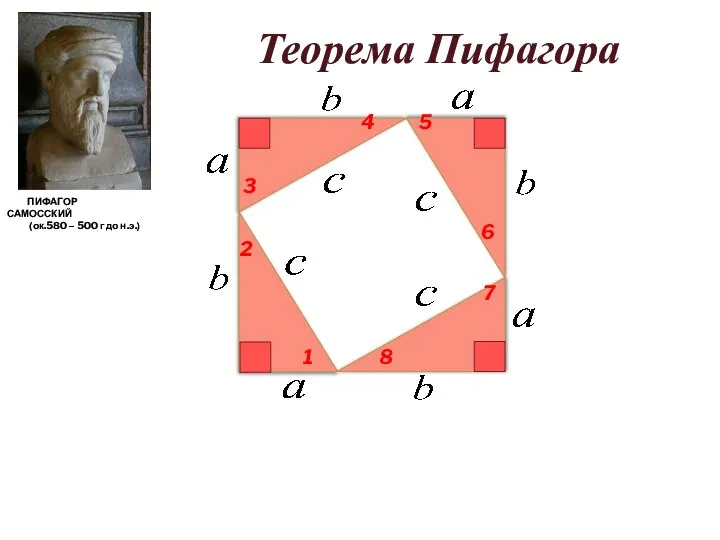
- 13. Теорема Пифагора Геометрическая формулировка теоремы Пифагора Площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей
- 14. ПИФАГОР САМОССКИЙ (ок.580 – 500 г до н.э.) Теорема Пифагора В прямоугольном треугольнике квадрат гипотенузы равен
- 15. Теорема Пифагора ПИФАГОР САМОССКИЙ (ок.580 – 500 г до н.э.) 1 2
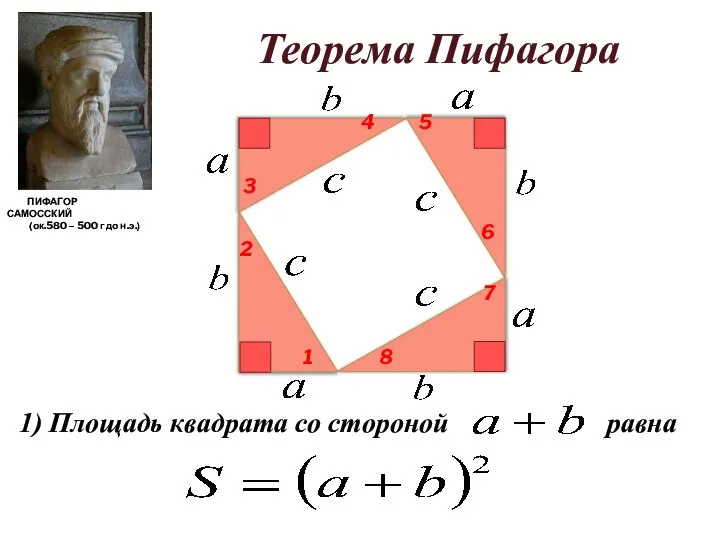
- 16. 1) Площадь квадрата со стороной ПИФАГОР САМОССКИЙ (ок.580 – 500 г до н.э.) Теорема Пифагора равна
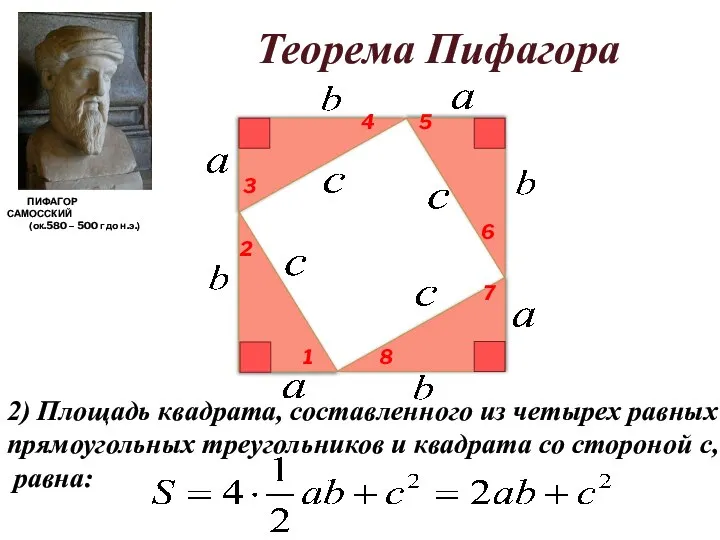
- 17. 2) Площадь квадрата, составленного из четырех равных прямоугольных треугольников и квадрата со стороной с, равна: ПИФАГОР
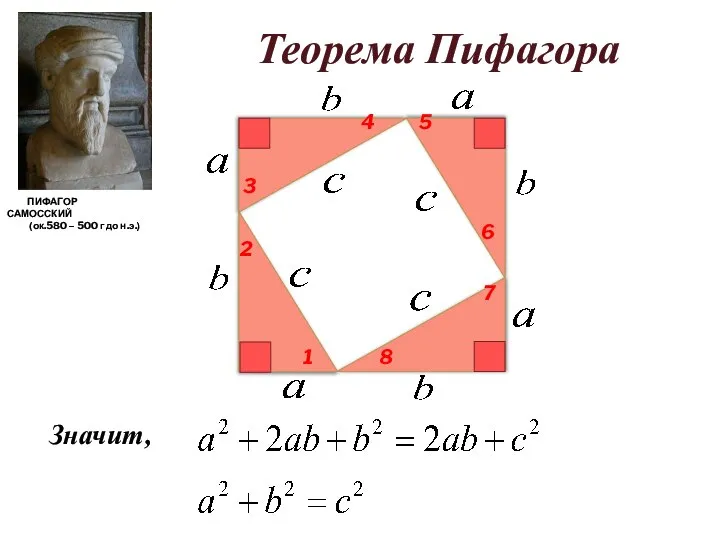
- 18. ПИФАГОР САМОССКИЙ (ок.580 – 500 г до н.э.) Теорема Пифагора Значит,
- 19. Задачи на чертежах
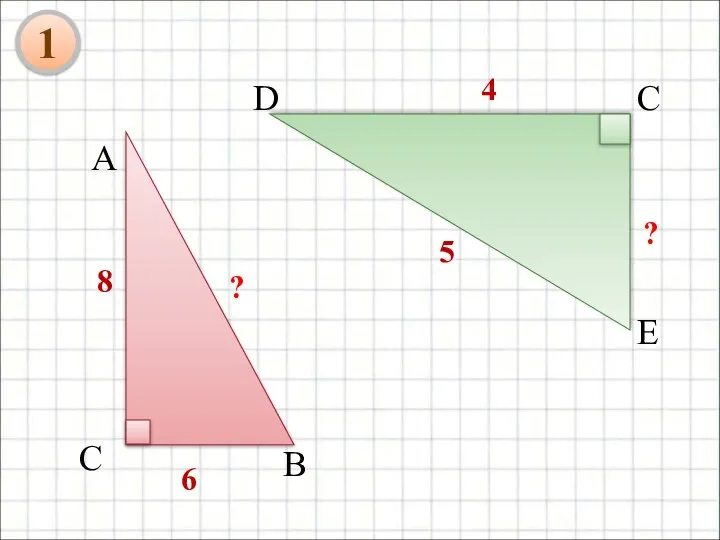
- 20. А 8 С В 6 ? 4 5 D C E ? 1
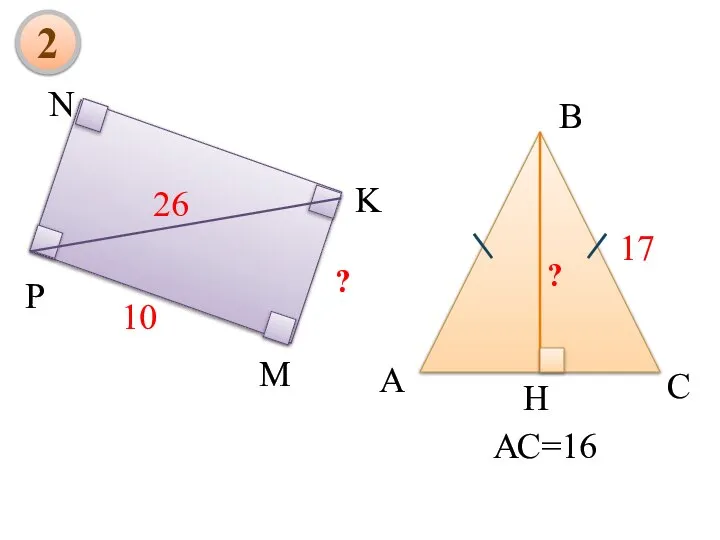
- 21. В А С N M K P 17 H ? АС=16 2
- 22. Дано: -равнобедренный AB=BC=17см, АС=16 см, BD- высота Найти: В 3
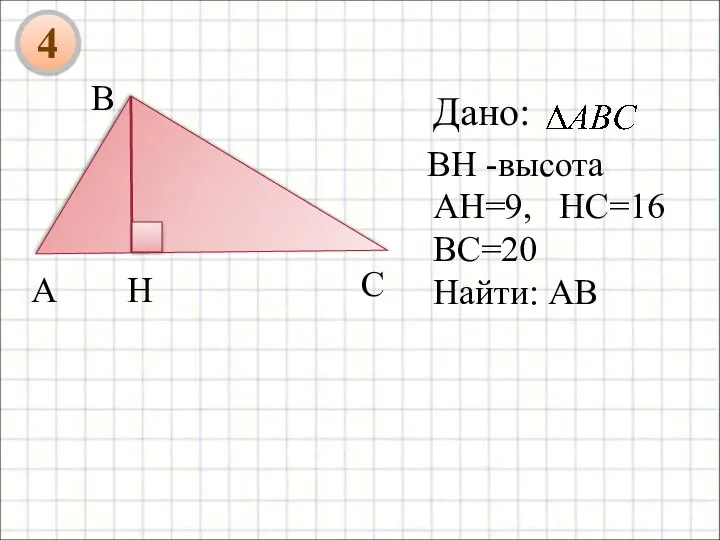
- 23. Дано: А В С ВH -высота H АH=9, HC=16 BC=20 Найти: АВ 4
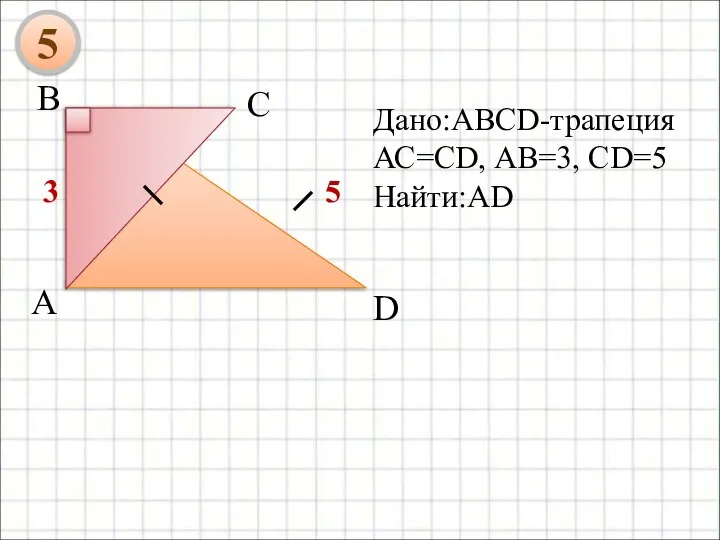
- 24. Дано:ABCD-трапеция АС=СD, АВ=3, CD=5 Найти:AD 5
- 26. Скачать презентацию








 Решение типовых задач Параллельность прямых и плоскостей
Решение типовых задач Параллельность прямых и плоскостей Линейное уравнение с одной переменной
Линейное уравнение с одной переменной Геометрические фигуры (интерактивная игра)
Геометрические фигуры (интерактивная игра) Лекция Алгебраические системы
Лекция Алгебраические системы Интегральная оценка угрозы биотерроризма. Цели, методы, задачи
Интегральная оценка угрозы биотерроризма. Цели, методы, задачи РўР’РёРњРЎ_Лекция 2_Теоремы Рѕ вероятностях СЃРожных событий (4)
РўР’РёРњРЎ_Лекция 2_Теоремы Рѕ вероятностях СЃРожных событий (4) Логарифмические неравенства. Решение заданий
Логарифмические неравенства. Решение заданий Презентация по математике "Приемы вычислений для случаев вида 60-24" -
Презентация по математике "Приемы вычислений для случаев вида 60-24" -  Математический анализ. Производная и первообразная
Математический анализ. Производная и первообразная Иллюзии и математические парадоксы
Иллюзии и математические парадоксы Путешествие по математическому морю (1)
Путешествие по математическому морю (1) Презентация на тему Прямая. Отрезок. Или приключения в стране ГЕОМЕТРИИ (1 класс)
Презентация на тему Прямая. Отрезок. Или приключения в стране ГЕОМЕТРИИ (1 класс)  Внетабличное деление
Внетабличное деление ЕГЭ 2020. Решение задания №9
ЕГЭ 2020. Решение задания №9 Система линейных уравнений с двумя переменными
Система линейных уравнений с двумя переменными Пределы
Пределы Определение предела последовательности
Определение предела последовательности формулы нахождения периметра прямоугольника, периметра квадрата
формулы нахождения периметра прямоугольника, периметра квадрата Probability Distributions
Probability Distributions Методы решения логарифмических уравнений
Методы решения логарифмических уравнений Complete each of the following:
Complete each of the following: СРС 2 ВСК 2. Задачи
СРС 2 ВСК 2. Задачи Формулы сокращенного умножения
Формулы сокращенного умножения Решение логарифмических уравнений
Решение логарифмических уравнений Генеральная средняя
Генеральная средняя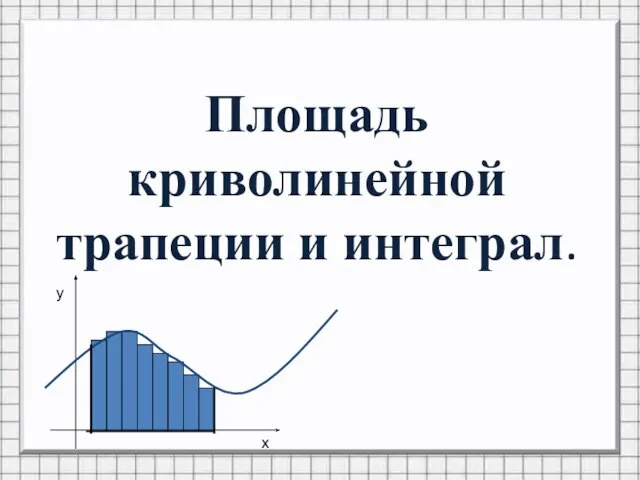 Площадь криволинейной трапеции и интеграл
Площадь криволинейной трапеции и интеграл Презентация на тему Математика вокруг нас 6 класс для учителя
Презентация на тему Математика вокруг нас 6 класс для учителя  Тригонометрические формулы
Тригонометрические формулы