Содержание
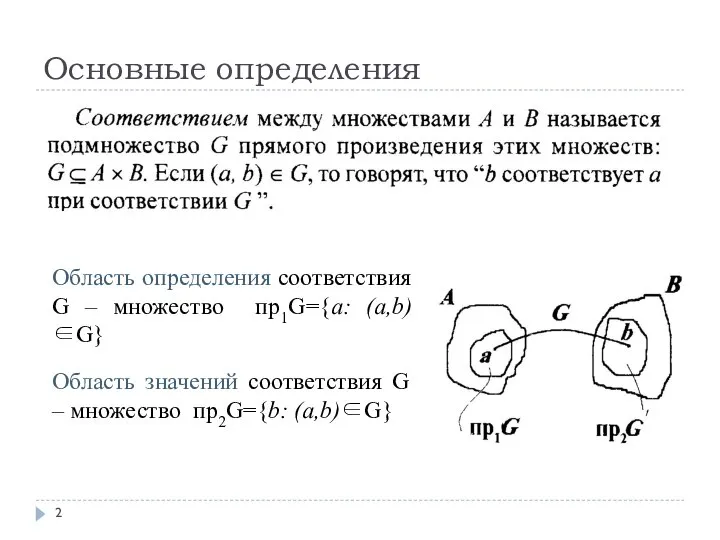
- 2. Основные определения Область определения соответствия G – множество пр1G={a: (a,b)∈G} Область значений соответствия G – множество
- 3. Основные определения Пример 1. Экзаменационная ведомость устанавливает следующее соответствие : А={Иванов, Петров, Сидоров, Конев, Синицын, Васечкин,
- 4. G={(Иванов, 4), (Петров, 2), (Сидоров, 3), (Конев, 4), (Васечкин, 3), (Макарова, 5)}. Область определения соответствия G
- 5. Основные определения В примере 1: образом Иванова является 4; образом Сидорова - 3 и т.д. Прообразом
- 6. Свойства соответствий Соответствие G⊆А×В называется всюду (полностью) определенным, если область определения совпадает с множеством А, т.е.
- 7. Свойства соответствий Определим свойства отношения в примере 1. Частично определено, так как нет образа для Синицына;
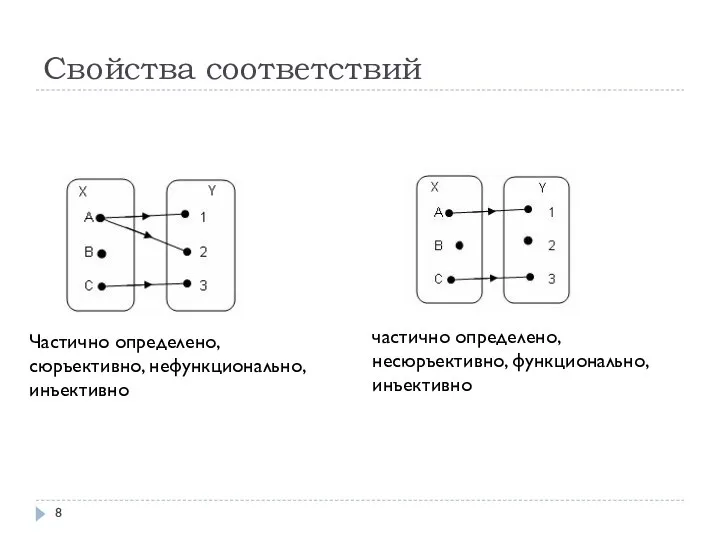
- 8. Свойства соответствий частично определено, несюръективно, функционально, инъективно Частично определено, сюръективно, нефункционально, инъективно
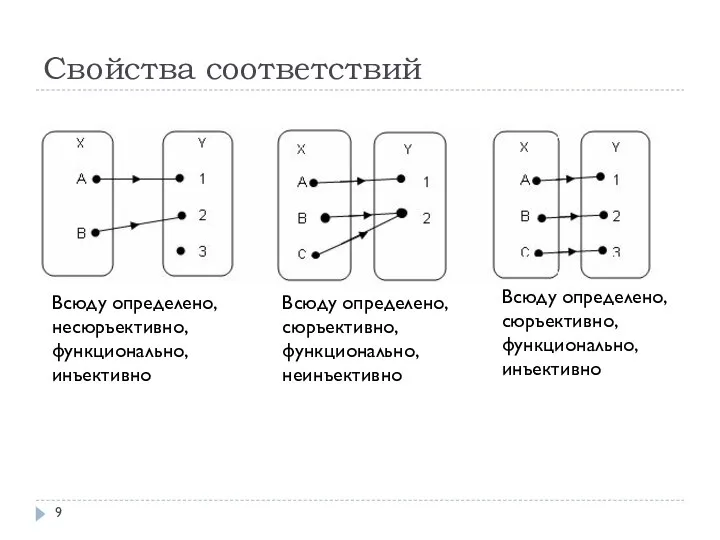
- 9. Свойства соответствий Всюду определено, несюръективно, функционально, инъективно Всюду определено, сюръективно, функционально, неинъективно Всюду определено, сюръективно, функционально,
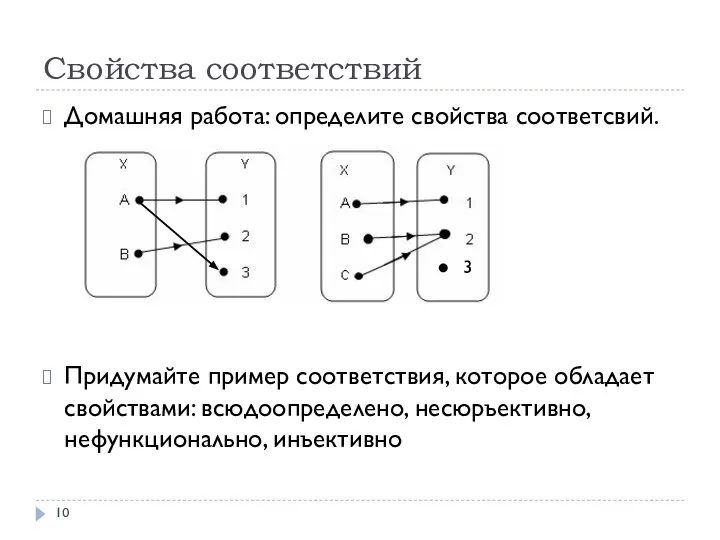
- 10. Домашняя работа: определите свойства соответсвий. Придумайте пример соответствия, которое обладает свойствами: всюдоопределено, несюръективно, нефункционально, инъективно 3
- 11. )
- 12. G⊆R+×R+ Найти образы и прообразы чисел: 0, 1, 2; отрезков: [0,1], [2,3]
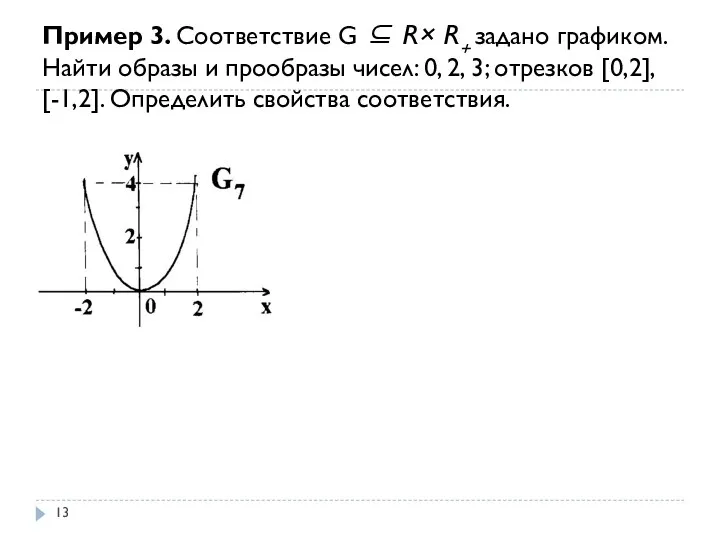
- 13. Пример 3. Соответствие G ⊆ R× R+ задано графиком. Найти образы и прообразы чисел: 0, 2,
- 14. Функции и отображения Функциональное соответствие называется функцией. Если функция f устанавливает соответствие между множествами А и
- 15. Функции и отображения Отображением А в В называется всюду определенная функция f : А→В (обозначается f
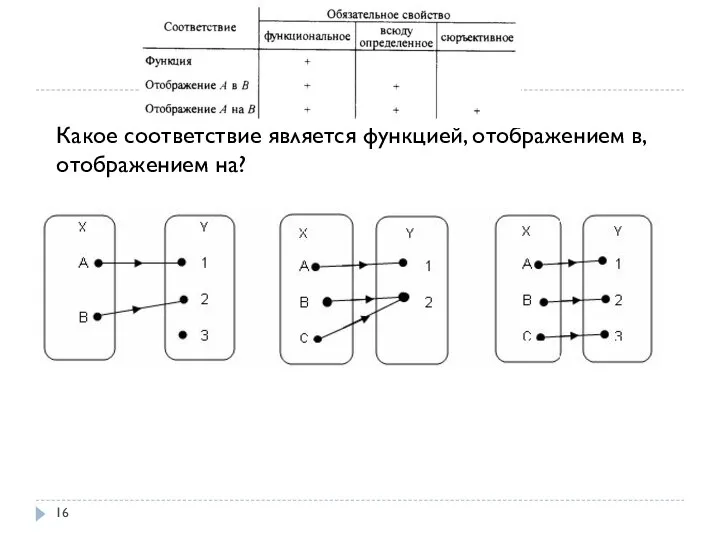
- 16. Какое соответствие является функцией, отображением в, отображением на?
- 17. Функции и отображения тип Как нужно определить эту функцию, чтобы она стала отображением N на N
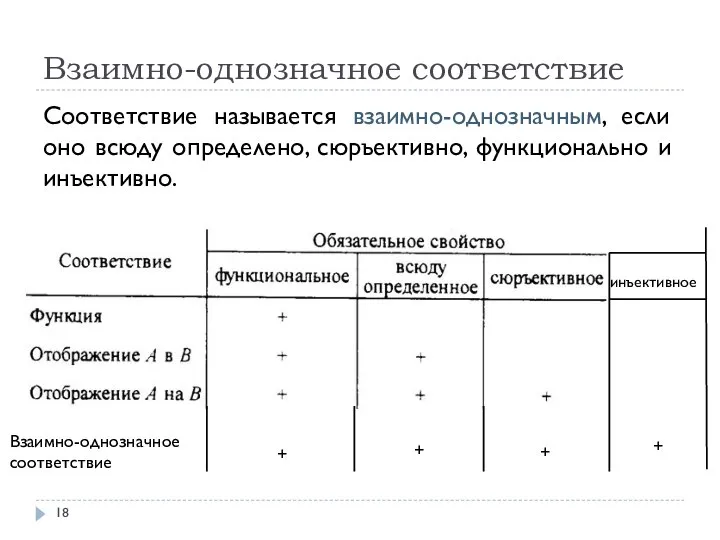
- 18. Взаимно-однозначное соответствие Соответствие называется взаимно-однозначным, если оно всюду определено, сюръективно, функционально и инъективно.
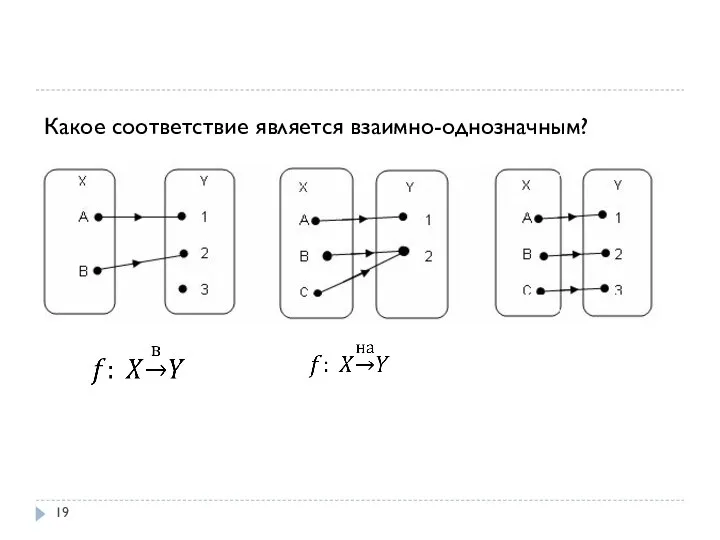
- 19. Какое соответствие является взаимно-однозначным?
- 20. Взаимно-однозначное соответствие
- 21. Мощность множеств Понятие мощности возникает при сравнении множеств по числу элементов. Мощностью конечного множества является число
- 22. Мощность множеств Этот факт позволяет: установить равенство мощностей двух множеств, не вычисляя этих множеств; вычислить мощность
- 23. Счетные множества Любое множество, равномощное множеству всех натуральных чисел, называют счетным. Мощность счетного множества обозначают ℵ0
- 24. Счетные множества Если элемент множества М есть ν(n) для некоторого n∈ N, то этот элемент множества
- 25. Счетные множества Пример. Множество всех нечетных натуральных чисел счетно. Нумерацию ν можно задать так: ν(n) =
- 26. Счетные множества Пример. Множество Z всех целых чисел счетно. Расположим элементы множества целых чисел в определенном
- 27. Счетные множества Пример. Множество Z всех целых чисел счетно. Нумерацию можно было установить так: Z={…, -5,
- 28. Счетные множества Примеры счетных множеств: Множество рациональных чисел счетно; Множество периодических дробей счетно; Множество всех натуральных
- 29. Счетные множества Докажем, что Множество пар натуральных чисел счетно.
- 30. Счетные множества Теорема . (а) Подмножество счетного множества конечно или счетно. (б) Всякое бесконечное множество содержит
- 31. Несчетные множества Теорема Кантора: Множество всех действительных чисел интервала (0,1) числовой оси несчетно. Всякое множество, эквивалентное
- 32. Примеры континуальных множеств: Множество действительных чисел; Множество иррациональных чисел ; Множество точек на отрезке [0,5]; Множество
- 34. Скачать презентацию






![G⊆R+×R+ Найти образы и прообразы чисел: 0, 1, 2; отрезков: [0,1], [2,3]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1059919/slide-11.jpg)
















 Теорема Пифагора
Теорема Пифагора У мольберта - математик
У мольберта - математик Преобразование выражения Asinx+Bcosx к виду Csin(x+t)
Преобразование выражения Asinx+Bcosx к виду Csin(x+t) Операции над множествами
Операции над множествами Параллелепипед и куб. 3 класс
Параллелепипед и куб. 3 класс Устный счет. Пропорция
Устный счет. Пропорция Проект по математике. Цифра 5. 1 класс
Проект по математике. Цифра 5. 1 класс Использование прикладных программ для оптимизации задач исследования. Контрольная работа
Использование прикладных программ для оптимизации задач исследования. Контрольная работа Решение треугольников
Решение треугольников Презентация на тему Тренажёр «Квадратные корни»
Презентация на тему Тренажёр «Квадратные корни»  Линии на плоскости
Линии на плоскости Решение систем линейных неравенств
Решение систем линейных неравенств Сечения куба плоскостью
Сечения куба плоскостью Решение иррациональных уравнений
Решение иррациональных уравнений Тригонометрические уравнения
Тригонометрические уравнения Основные понятия комбинаторики
Основные понятия комбинаторики Таблицы. Геометрия
Таблицы. Геометрия Задачи на готовых чертежах. Подобные треугольники
Задачи на готовых чертежах. Подобные треугольники Логические задачи. 1 класс
Логические задачи. 1 класс Квадратный корень из произведения и дроби
Квадратный корень из произведения и дроби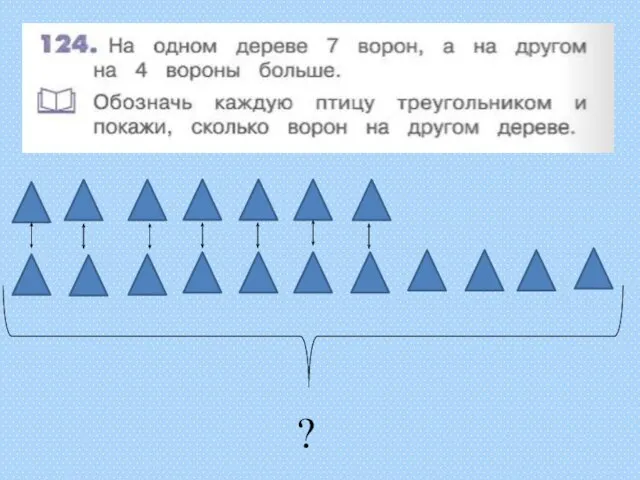 Треугольники, задача
Треугольники, задача ВЛИЯНИЕ КОЭФФИЦИЕНТОВ а, b и с НА РАСПОЛОЖЕНИЕ ГРАФИКА КВАДРАТИЧНОЙ ФУНКЦИИ
ВЛИЯНИЕ КОЭФФИЦИЕНТОВ а, b и с НА РАСПОЛОЖЕНИЕ ГРАФИКА КВАДРАТИЧНОЙ ФУНКЦИИ Сложение и вычитание вида +1 -1
Сложение и вычитание вида +1 -1 Сложение дробей с разными знаменателями
Сложение дробей с разными знаменателями Режим поступления заявок
Режим поступления заявок Математика. 1 класс
Математика. 1 класс Правила нахождения производной
Правила нахождения производной Метод Галеркина для дифференциально-операторного уравнения третьего порядка
Метод Галеркина для дифференциально-операторного уравнения третьего порядка