Содержание
- 2. Понятие статистического вывода Статистический вывод: использование выборочных данных для получения и формализации знаний о свойствах генеральной
- 3. Метод Монте-Карло Генеративный (регенеративный) подход: исследование статистических свойств на основе «размножения» заданной выборки Механизмы генерации: На
- 4. Случайные числа Значения γ равномерно распределенной случайной величины в интервале [0,1]: Псевдослучайные числа (ПСЧ): на основе
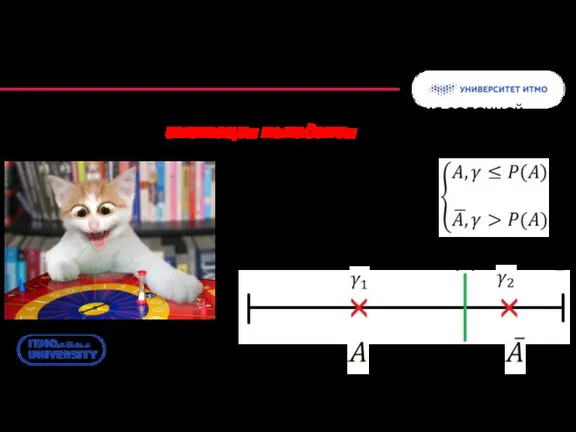
- 5. Моделирование случайных событий Выбор варианта реализации события по значению γ: Геометрическая интерпретация случайного события заданной вероятности
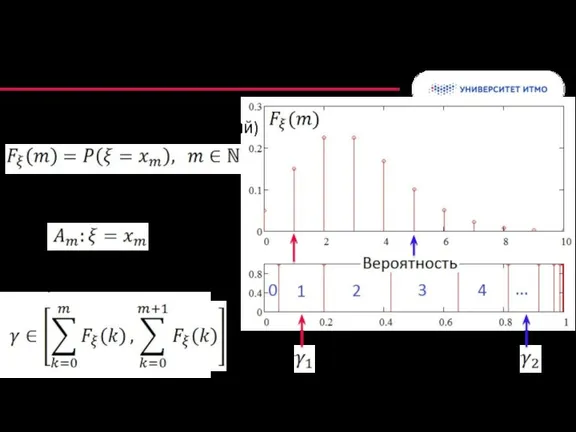
- 6. Моделирование дискретных величин Закон распределения (вероятности набора событий) Выбор реализации события при попадании точки в интервал
- 7. Моделирование непрерывных величин (1/3) Дискретно-равномерное приближение (на основе группированных данных) Выбор номера столбца i Выбор значения
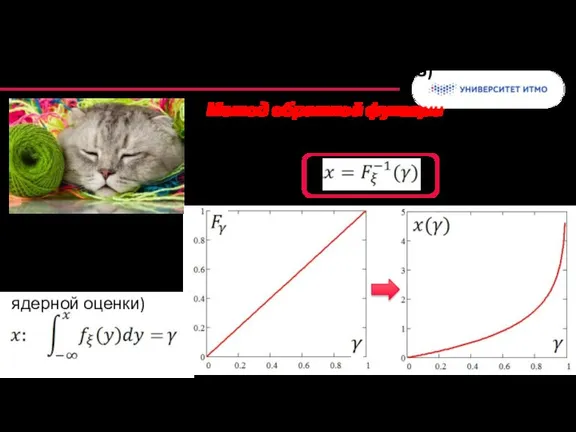
- 8. Моделирование непрерывных величин (2/3) Метод обратной функции (на основе преобразования квантилей)
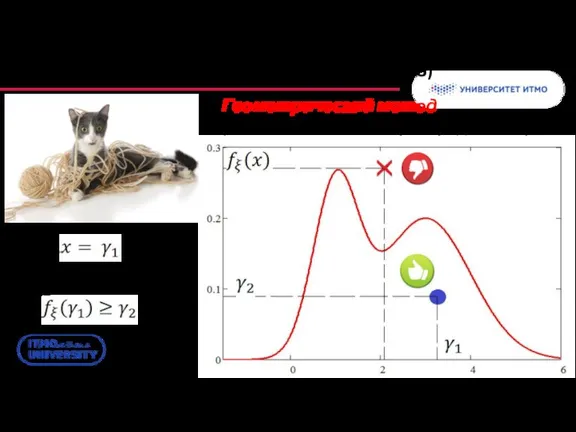
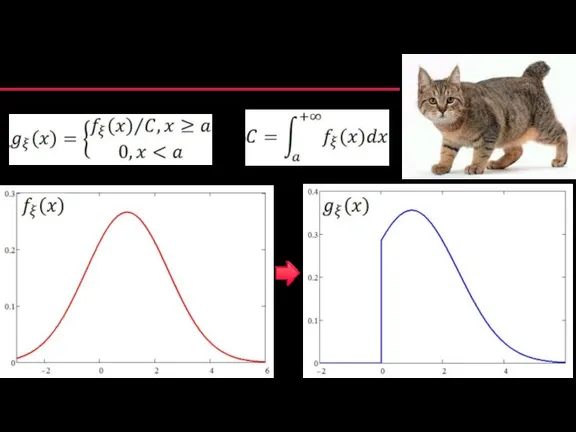
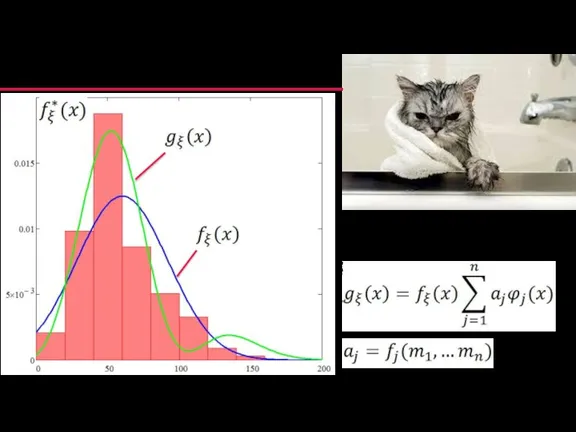
- 9. Моделирование непрерывных величин (3/3) Геометрический метод (на основе плотности распределения) при условии, что
- 10. Моделирование гауссовых случайных величин 1) На основе центральной предельной теоремы: Нормированное распределение Гаусса N(0,1)
- 11. Интервальное оценивание на основе Монте-Карло Для избранной статистики : Сгенерировать M выборок Выбрать метод моделирования случайной
- 12. Задача об отборе на выставку кошек (1/2) Найти интервальные оценки математического ожидания и дисперсии для: (а)
- 13. Задача об отборе на выставку кошек (2/2) Для малых выборок асимптотические формулы некорректны, а метод Монте-Карло
- 14. Непараметрические методы: бутстреп Формирование М псевдовыборок на основе случайного выбора с возвращением из исходной выборки: Псевдовыборки
- 15. Непараметрические методы: джекнайф Формирование N подвыборок путем выкалывания одного из членов исходной выборки: Подвыборки Методическая проблема
- 16. Обобщение: генеративная статистика Метод Монте-Карло: универсальный инструмент статистического оценивания, когда аналитика не справляется Методы моделирования случайных
- 17. Александр Валерьевич Бухановский, Анна Владимировна Калюжная [email protected] Автор признателен всем котикам (и хозяевам) за возможность некоммерческого
- 18. ЗАНЯТИЕ 3 ТЕОРИЯ И ПРАКТИКА СТАТИСТИЧЕСКИХ ВЫВОДОВ Александр Валерьевич Бухановский, Анна Владимировна Калюжная Раздел 2. Проверка
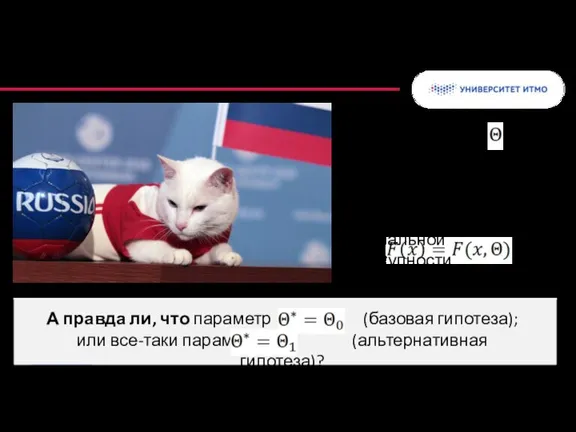
- 19. Проверка статистических гипотез = ? Нулевая (базовая) гипотеза ?
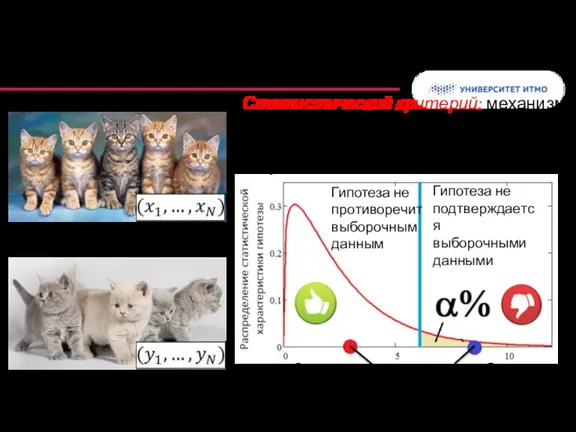
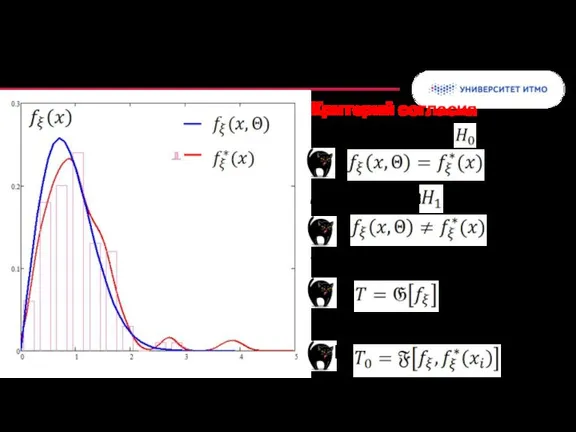
- 20. Гипотеза о виде распределения (пример) Альтернатива : Выборочная характеристика Теоретическая характеристика Критерий согласия
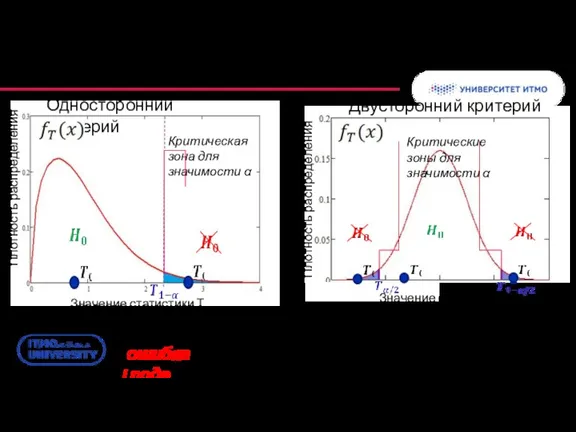
- 21. Критерии: сравнение характеристик Односторонний критерий Двусторонний критерий Ошибка проверки непараметрических гипотез (ошибка I рода) – с
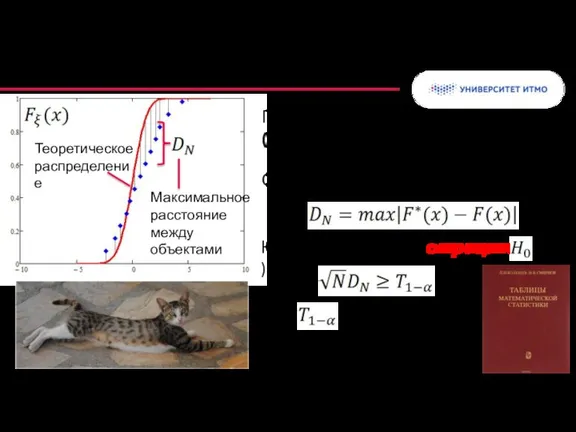
- 22. Критерий Колмогорова Проверка гипотезы о виде (модели) распределения Статистическая характеристика: - квантиль распределения Колмогорова Максимальное расстояние
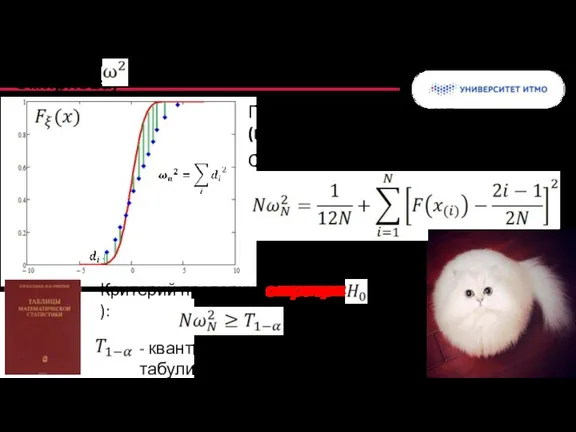
- 23. Критерий (Крамера-вон Мизеса-Смирнова) Проверка гипотезы о виде (модели) распределения Статистическая характеристика: - квантиль табулированного распределения
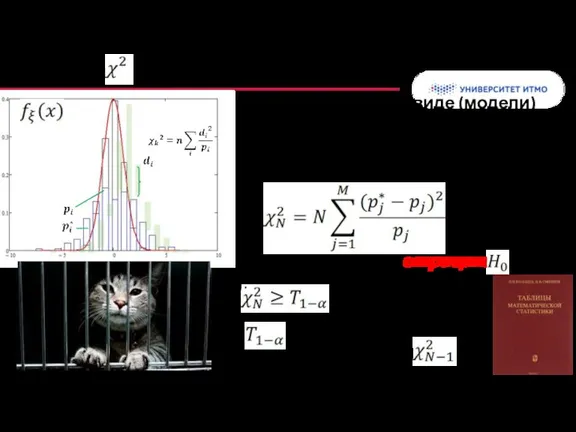
- 24. Значение случайной величины x Проверка гипотезы о виде (модели) распределения по группированным данным Статистическая характеристика :
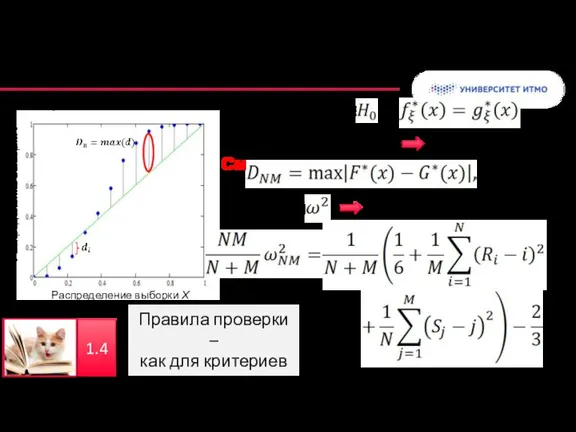
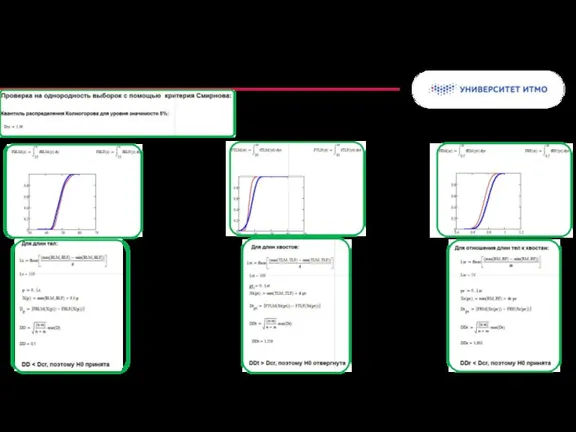
- 25. Вероятностный биплот Критерии для проверки однородности Критерий Колмогорова Смирнова Критерий Розенблатта Правила проверки – как для
- 26. Задача о поддельных мейн-кунах (1/3) В одном питомнике разводят крупных котов и продают как мейн-кунов. Однако
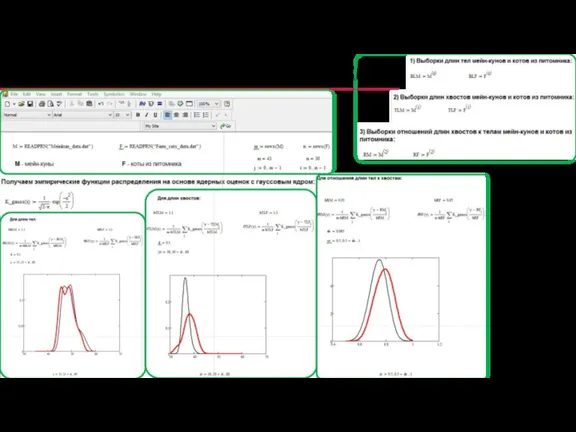
- 27. Задача о поддельных мейн-кунах (2/3)
- 28. Задача о поддельных мейн-кунах (3/3)
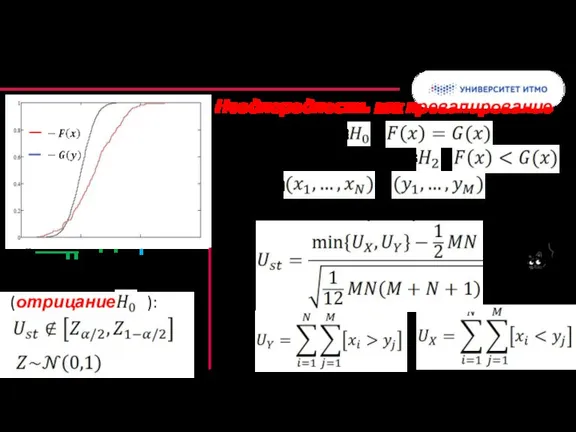
- 29. Критерий ранговых сумм Вилкоксона Альтернативная гипотеза : Неоднородность как превалирование Статистическая характеристика: Критерий проверки (отрицание ):
- 30. Обобщение: непараметрические критерии Решаемые задачи: проверка соответствие распределения определенному закону, проверка однородности двух выборок. Все критерии
- 31. Александр Валерьевич Бухановский, Анна Владимировна Калюжная [email protected] Автор признателен всем котикам (и хозяевам) за возможность некоммерческого
- 32. ЗАНЯТИЕ 3 ТЕОРИЯ И ПРАКТИКА СТАТИСТИЧЕСКИХ ВЫВОДОВ Александр Валерьевич Бухановский, Анна Владимировна Калюжная Раздел 3. Проверка
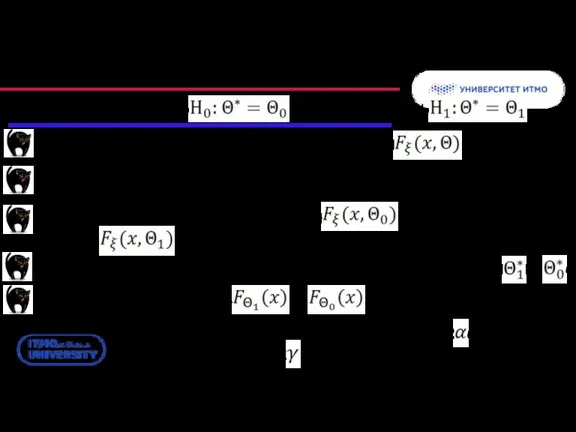
- 33. Логика параметрических критериев Объект исследования – набор параметров , характеризующих модель распределения генеральной совокупности
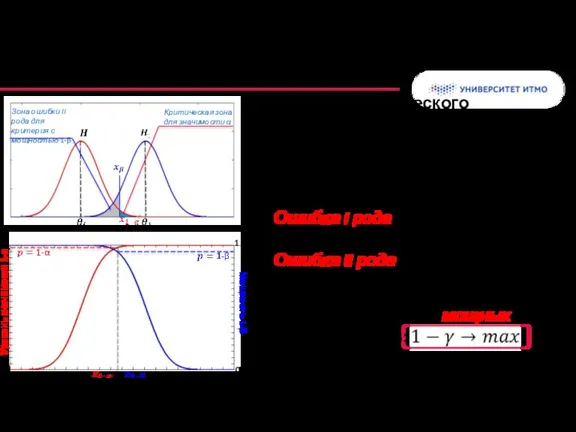
- 34. Построение наиболее мощных (в своем классе) критериев: Критическая зона для значимости α Зона ошибки II рода
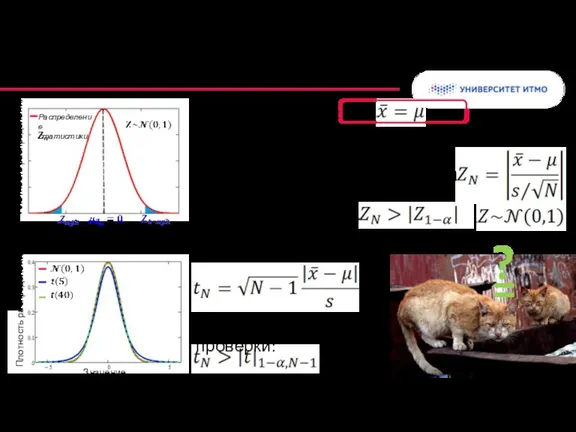
- 35. Распределение статистики Плотность распределения Значение статистики Плотность распределения Значение СВ Критерий для среднего значения Базовая гипотеза:
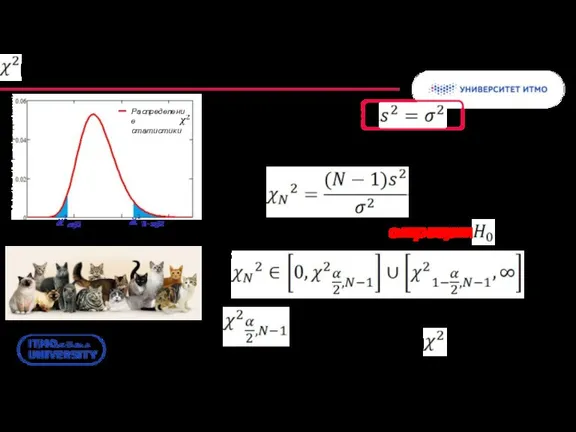
- 36. - табличная квантиль распределения с N-1 степенью свободы Распределение статистики Плотность распределения Значение статистики Критерий для
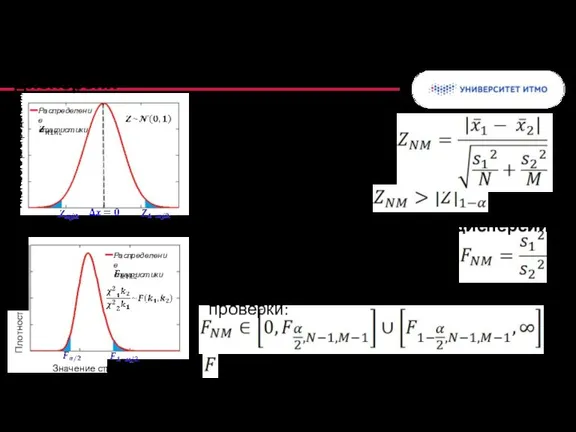
- 37. Распределение статистики Плотность распределения Значение статистики Плотность распределения Значение статистики Распределение статистики Критерий для равенства средних
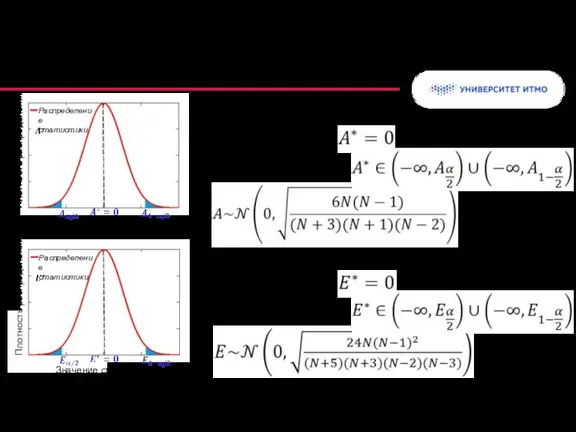
- 38. Суждение о выраженности пика распределения Базовая гипотеза: Суждение об асимметрии распределения Базовая гипотеза: Распределение статистики Плотность
- 39. Метод Монте-Карло для проверки гипотез Для базовой гипотезы и альтернативы : Сгенерировать M выборок по закону
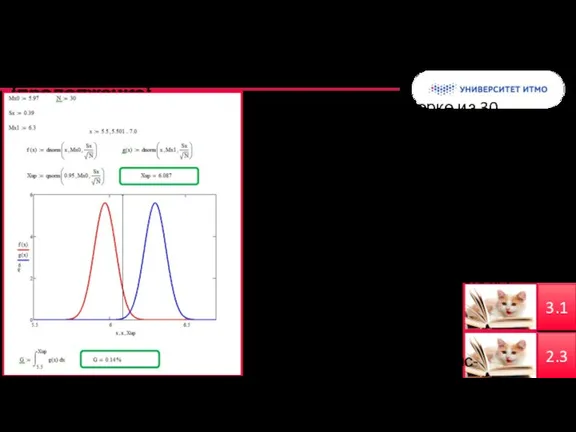
- 40. Задача об отборе на выставку кошек (продолжение) Средний вес по выборке из 30 кошек составил 5.97
- 41. Развитие: статистические игры и решения Риск: средние потери при решении Смысл игры: предугадать реакцию «противника» (значение
- 42. Александр Валерьевич Бухановский, Анна Владимировна Калюжная [email protected] Автор признателен всем котикам (и хозяевам) за возможность некоммерческого
- 43. ЗАНЯТИЕ 3 ТЕОРИЯ И ПРАКТИКА СТАТИСТИЧЕСКИХ ВЫВОДОВ Александр Валерьевич Бухановский, Анна Владимировна Калюжная Раздел 4. Конструктивные
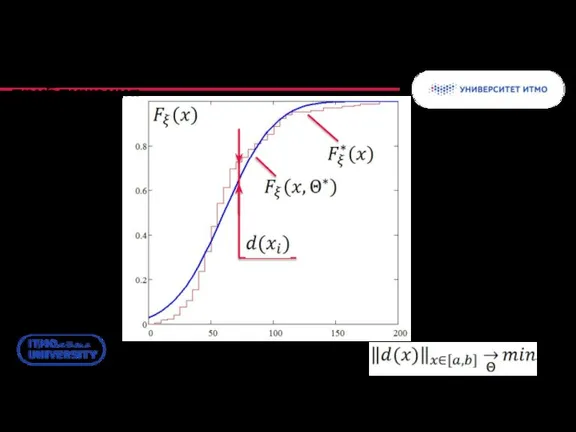
- 44. Подбор распределения как задача приближения Минимизация нормы невязки:
- 45. Идея метода наименьших квадратов (МНК) Невязка как евклидово расстояние: Идея метода (минимизация суммы квадратов невязок по
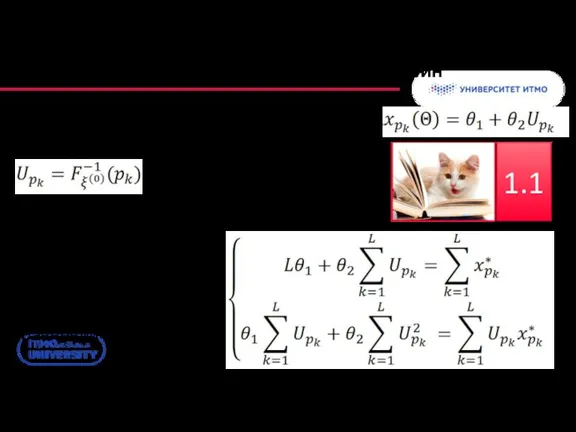
- 46. МНК для линейно-масштабируемых величин Квантиль линейно-масштабируемой величины: - квантиль нормированного модельного распределения Реализация МНК: система из
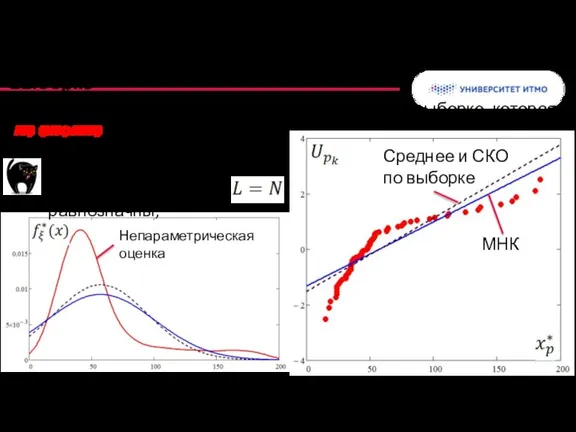
- 47. Простейшее приближение: МНК по всей выборке МНК Среднее и СКО по выборке Задача: приблизить модельное распределение
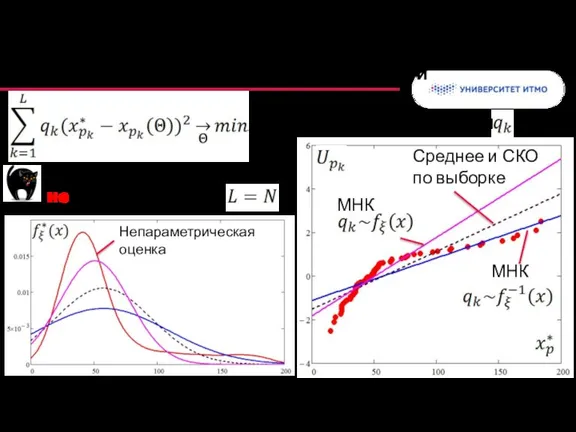
- 48. Взвешенный МНК: учитываем особенности Целевая функция с весами Среднее и СКО по выборке МНК МНК Выборочные
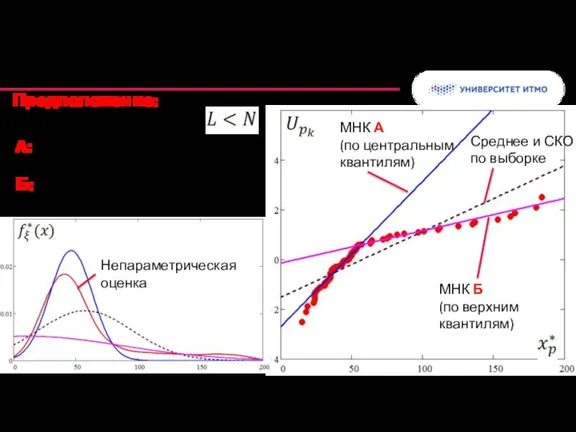
- 49. МНК по избранным квантилям Среднее и СКО по выборке МНК А (по центральным квантилям) МНК Б
- 50. Модель усеченного распределения
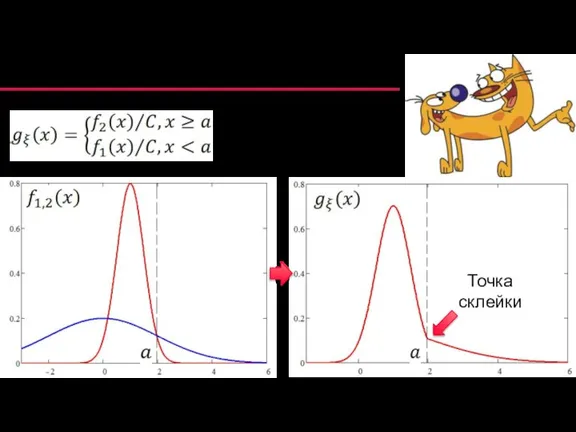
- 51. Модель склейки распределений С – нормировочная константа Точка склейки
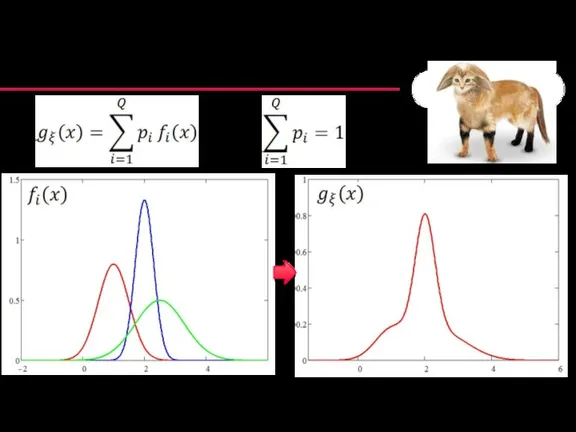
- 52. Модель смеси распределений
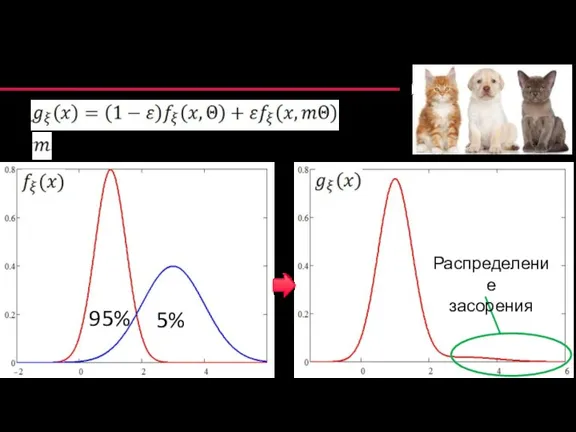
- 53. Модель распределения с засорением 5% 95% - параметр масштаба засорения
- 54. Модель в форме ряда Эджворта Разложение в окрестности модельного распределения
- 55. Обобщение: конструктивные распределения Метод МНК: удачный механизм для «натягивания» моделей распределений на реальные данные Механизмы управления
- 56. Александр Валерьевич Бухановский [email protected] Автор признателен всем котикам (и хозяевам) за возможность некоммерческого использования их изображений,
- 57. ЗАНЯТИЕ 3 ТЕОРИЯ И ПРАКТИКА СТАТИСТИЧЕСКИХ ВЫВОДОВ Александр Валерьевич Бухановский, Анна Владимировна Калюжная Раздел 5. Практическая
- 58. Инструменты компьютерной математики MATLAB R Python MS Excel Statistica
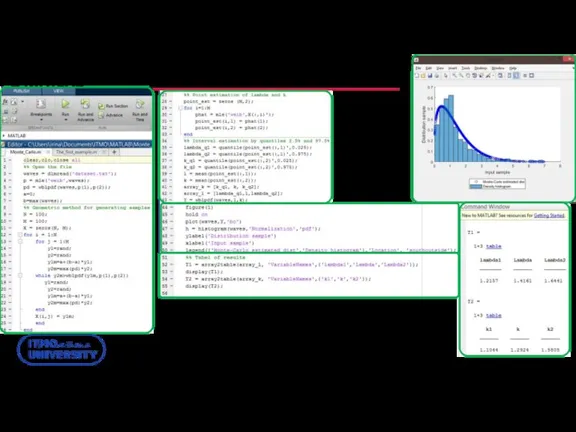
- 59. Интервальное оценивание на основе Монте-Карло в MATLAB
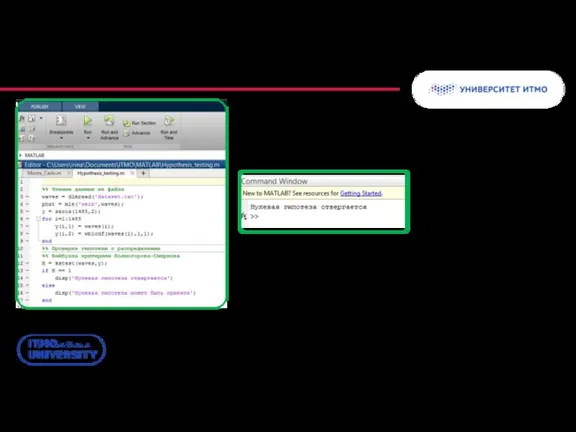
- 60. Тест Колмогорова-Смирнова в MATLAB
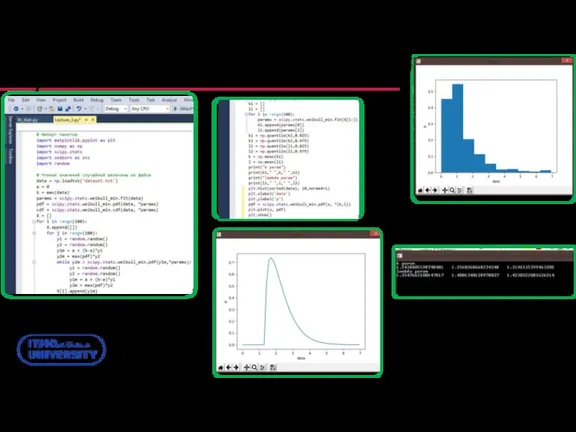
- 61. Интервальное оценивание на основе Монте-Карло в Python
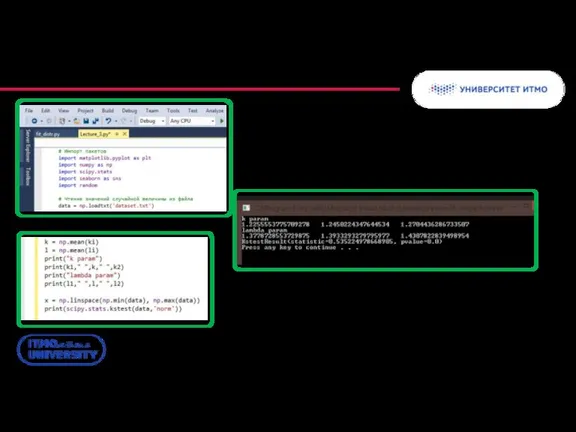
- 62. Тест Колмогорова-Смирнова в Python
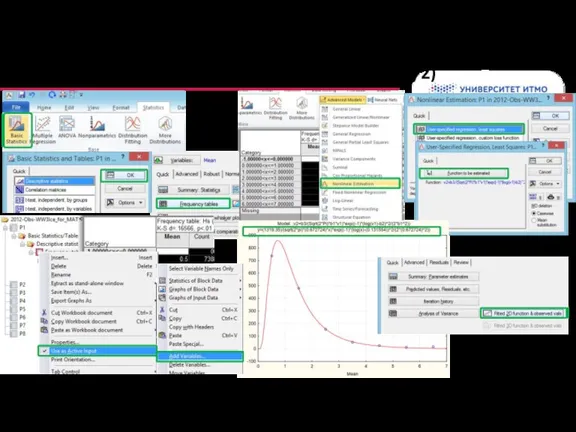
- 63. Колонтитул Метод наименьших квадратов в Statistica(1/2)
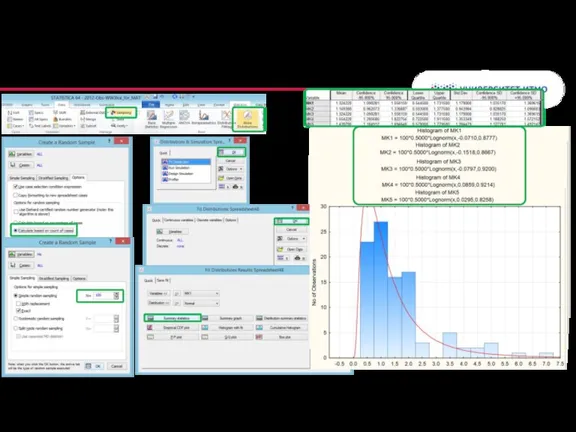
- 64. Колонтитул Метод Монте-Карло в Statistica(2/2)
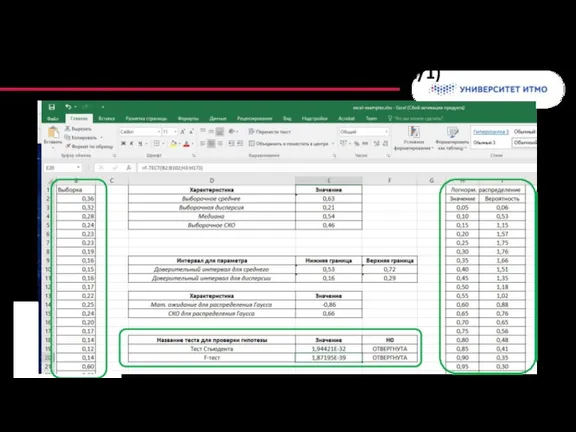
- 65. Проверка статистических гипотез в Excel (1/1)
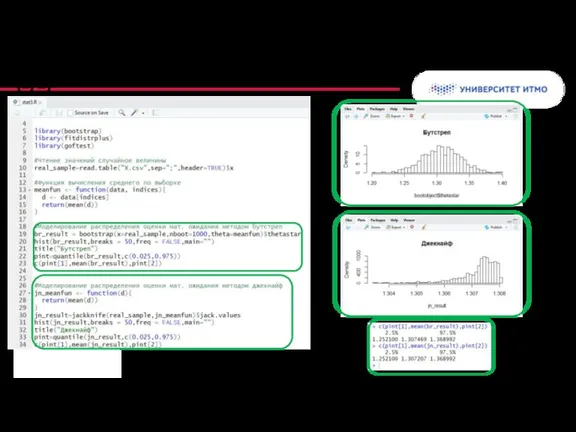
- 66. Интервальное оценивание на основе Монте-Карло в R (1/2)
- 68. Скачать презентацию

![Случайные числа Значения γ равномерно распределенной случайной величины в интервале [0,1]: Псевдослучайные](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1144051/slide-3.jpg)





















 Ситуация успеха на уроках математики как средство повышения качества образования
Ситуация успеха на уроках математики как средство повышения качества образования Методика изучения объема
Методика изучения объема Матрицы
Матрицы Семейство четырехугольников
Семейство четырехугольников ЕГЭ 2014. Задачи первой и второй части (Вариант 43)
ЕГЭ 2014. Задачи первой и второй части (Вариант 43)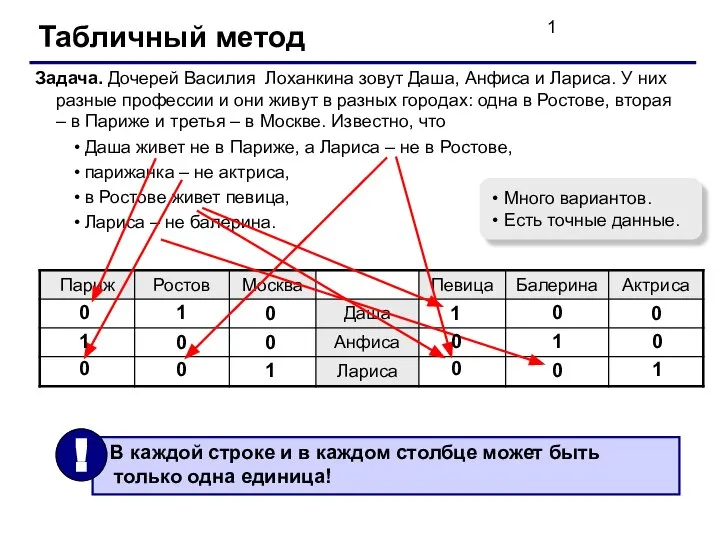 Табличный метод решения логических задач
Табличный метод решения логических задач Исследование корреляции
Исследование корреляции Вычислите логарифм. Практическая работа
Вычислите логарифм. Практическая работа Сравнение предметов по некоторой величине без её измерения: выше - ниже, шире - уже
Сравнение предметов по некоторой величине без её измерения: выше - ниже, шире - уже 2 погрешности ру с
2 погрешности ру с Значение переменной после выполнения алгоритма
Значение переменной после выполнения алгоритма Презентация на тему Вычисление объемов пространственных тел
Презентация на тему Вычисление объемов пространственных тел  Деление дробей. 6 класс
Деление дробей. 6 класс Свойства действий над числами
Свойства действий над числами Vorlesung. Blatt 2
Vorlesung. Blatt 2 Построение Сечения
Построение Сечения Преобразования неравенств
Преобразования неравенств Первый признак равенства треугольников
Первый признак равенства треугольников Презентация на тему Меры длинны Древней Руси
Презентация на тему Меры длинны Древней Руси  Презентация на тему Подготовка к ЕГЭ по математике
Презентация на тему Подготовка к ЕГЭ по математике  ВКР: Исследование нормального строения конечных групп
ВКР: Исследование нормального строения конечных групп Задачи с величинами: цена, количество, стоимость
Задачи с величинами: цена, количество, стоимость Решение задач
Решение задач Дифференциальные уравнения высших порядков
Дифференциальные уравнения высших порядков Математический квест Хакерская атака
Математический квест Хакерская атака Решение задач на проценты. Концентрация
Решение задач на проценты. Концентрация Классификация оптимизационных задач
Классификация оптимизационных задач Квадрат. Основные свойства квадрата
Квадрат. Основные свойства квадрата