ZOLOTOE_SEChENIE_VOKRUG_NAS

«…Геометрия владеет двумя сокровищами –
теоремой Пифагора и золотым сечением,
и если первое из них можно сравнить с мерой золота, то второе – с драгоценным камнем…».
Иоганн Кеплер
Цель проекта – выявить «золотое сечение» в математике, природе, архитектуре, искусстве.
Задачи:
1. Изучить понятия «пропорция»; «золотое сечение».
2. Исследовать присутствие золотого сечения в различных областях жизни человека.
3. Научиться анализировать и делать выводы.
Предметы исследования: математика, искусство, живопись, архитектура, природа.

Что такое золотое сечение?
Деление отрезка в среднем и крайнем отношении
называют золотой пропорцией.
В истории утвердилось ещё одно название – «золотое сечение».
В математике пропорцией называют равенство двух отношений: a:b = c:d.
АС : АВ = СВ : АС, получается верная пропорция.
Это отношение и названо золотым сечением.
Золотое сечение - это такое деление отрезка на неравные части, при котором длина его большей части так относится к длине всего отрезка, как длина меньшей части к большей.
Или обратное отношение:
меньший отрезок так относится к большему, как больший ко всему.
Это отношение приближенно равно 5/8 или 0,618…
Обратное отношение приближенно равно 1,6180339887…

История возникновения понятия золотого сечения.
Пифагор
Ле Корбюзье
Евклид
Леонардо да Винчи
Леонардо Фибоначчи

Применение принципов золотого сечения в различных сферах жизни

Золотой прямоугольник
Золотой прямоугольник - прямоугольник, отношение сторон которого равно φ: книги, открытки, плитки шоколада, монитор компьютера, экран телевизора, бумажник и множество других предметов.
Если построить прямоугольник со сторонами, соотношение которых будет равно пропорции золотого сечения, и вписать в него ещё один «золотой прямоугольник», в тот — ещё один, и так до бесконечности внутрь и наружу, то по угловым точкам прямоугольников можно провести спираль. Интересно то, что такая спираль совпадёт со срезом раковины наутилуса, а также другими встречающимися в природе спиралями

Ряд Фибоначчи
Ряд чисел 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 и т.д. известен как ряд Фибоначчи.
Особенность последовательности чисел состоит в том, что каждый ее член, начиная с третьего, равен сумме двух предыдущих 2 + 3 = 5; 3 + 5 = 8; 5 + 8 = 13, 8 + 13 = 21; 13 + 21 = 34 и т.д., а отношение смежных чисел ряда приближается к отношению золотого деления.
Так, 21: 34 = 0,617, а 34: 55 = 0,618.
Это отношение обозначается символом φ.
Только это отношение - 0,618: 0,382 - дает непрерывное деление отрезка прямой в золотой пропорции, увеличение его или уменьшение до бесконечности, когда меньший отрезок так относится к большему, как больший ко всему.

Золотое сечение в живописи
Леонардо да Винчи. Картина "Джоконда".
Композиция портрета построена на «золотых треугольниках».

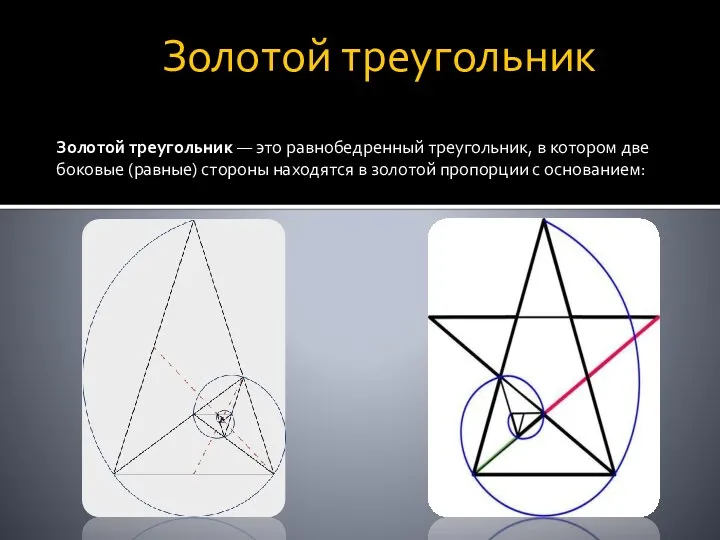
Золотой треугольник
Золотой треугольник — это равнобедренный треугольник, в котором две боковые (равные) стороны находятся в золотой пропорции с основанием:

Золотое сечение
в архитектуре
Парфенон (V в. до н. э.).

Золотое сечение
в архитектуре
Храм, построенный по принципу золотого сечения. При его высоте в 10 метров, высота барабана с куполом будут равны 3,82 см, а высота основания строения будет 6,18 см.