Содержание
- 2. Дискре́тная матема́тика — часть математики, изучающая дискретные — часть математики, изучающая дискретные математические структуры — часть
- 3. Исходные понятия теории множеств Понятие множества, подмножества, собственного подмножества
- 4. Понятие множества является одним из наиболее общих и наиболее важных математических понятий. Оно было введено в
- 5. Множества обычно обозначаются заглавными латинскими буквами. Если элемент x принадлежит множеству A, то это обозначается: х∈А
- 6. Пустое множество Среди множеств выделяют особое множество - пустое множество. Пустое множество- множество, не содержащее ни
- 7. Пустое множество является частью любого множества. Это множество настолько важное, что для него даже придумали особый
- 8. Определенные, конечные, бесконечные множества Множество считается определенным, если указаны все его элементы. Эти элементы могут быть
- 9. Пример Множество натуральных чисел является бесконечным. Упорядоченное множество - множество, каждому элементу которого поставлено в соответствие
- 10. различные способы задания множеств Пример: Множество учеников данного класса определяется их списком в классном журнале, множество
- 11. Задание множеств их характеристическим свойством иногда приводит к осложнениям: Может случиться, что два различных характеристических свойства
- 12. Множества А и В равны, если они состоят из одних и тех же элементов. Пример: Равными
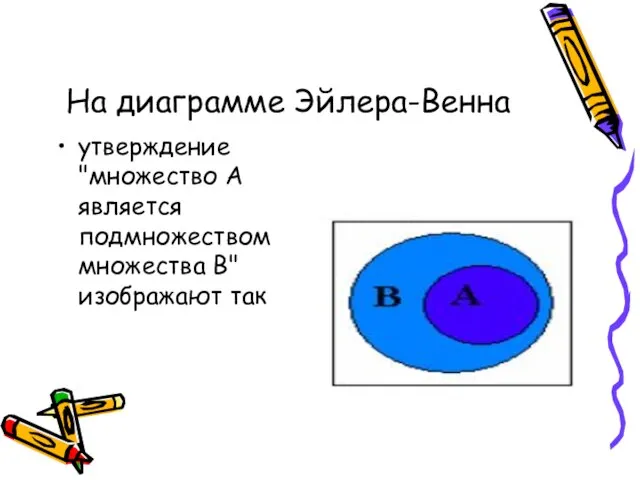
- 13. На диаграмме Эйлера-Венна утверждение "множество А является подмножеством множества В" изображают так
- 14. Основные теоретико-множественные операции 1. Объединение 2. Пересечение 3. Разность 4. Дополнение.
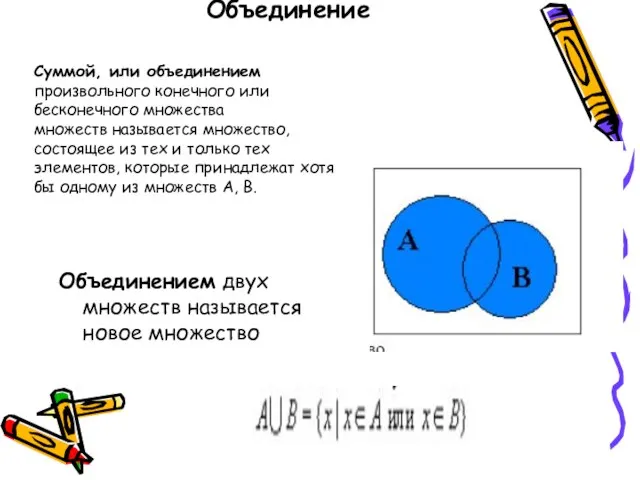
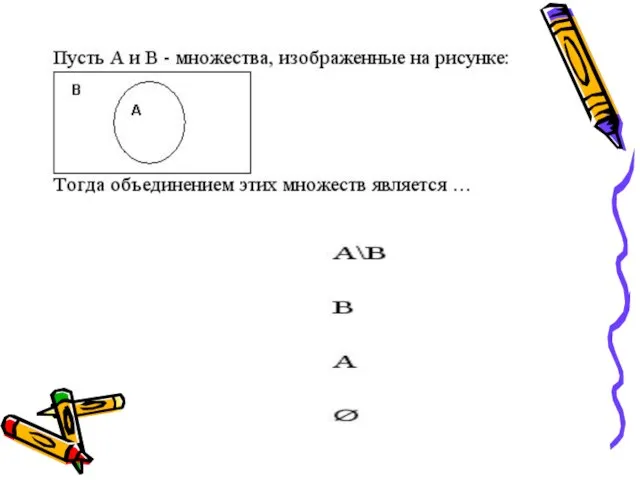
- 15. Объединение Объединением двух множеств называется новое множество Суммой, или объединением произвольного конечного или бесконечного множества множеств
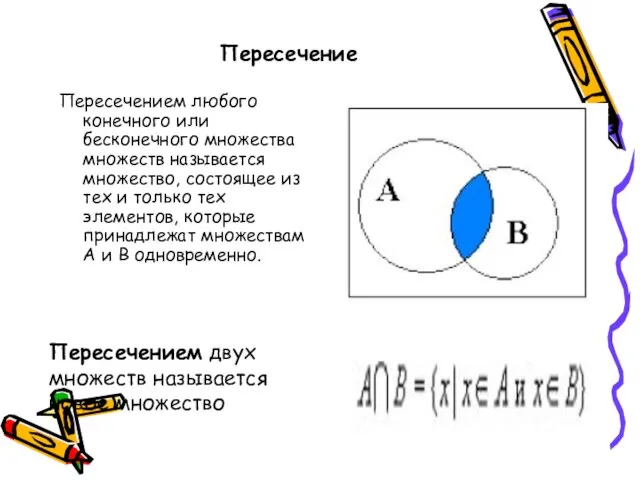
- 16. Пересечение Пересечением любого конечного или бесконечного множества множеств называется множество, состоящее из тех и только тех
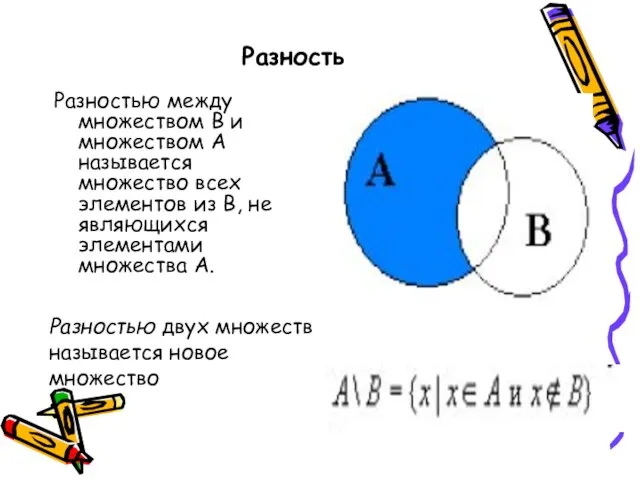
- 17. Разность Разностью между множеством В и множеством А называется множество всех элементов из В, не являющихся
- 18. Дополнение Если класс объектов, на которых определяются различные множества обозначить (Универсум), то дополнением множества называют разность
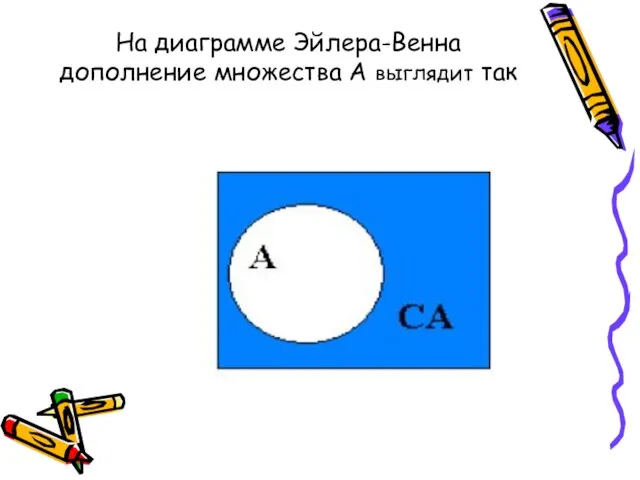
- 19. На диаграмме Эйлера-Венна дополнение множества А выглядит так
- 27. Алгебраические свойства операций над множествами Т. 1.1. Для любых подмножеств А, В и С универсального множества
- 29. Скачать презентацию



















 Применение теории вероятностей в анализе спортивных событий
Применение теории вероятностей в анализе спортивных событий Уравнение окружности и прямой
Уравнение окружности и прямой Вписанные окружности (решение задач)
Вписанные окружности (решение задач) Презентация на тему Свойства функций и их графики
Презентация на тему Свойства функций и их графики  Геометрическая интерпретация содержания задачи – условие успешного обучения каждого школьника решению математической задачи
Геометрическая интерпретация содержания задачи – условие успешного обучения каждого школьника решению математической задачи Математическое моделирование. Основные положения
Математическое моделирование. Основные положения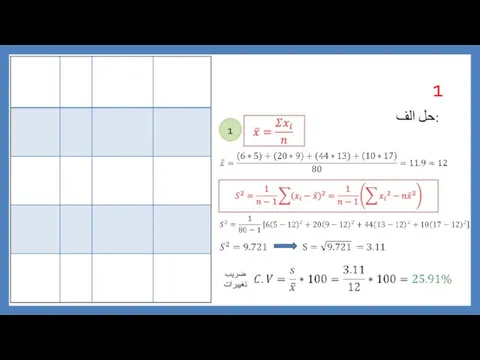 حل تمرین آمار
حل تمرین آمار Числовая последовательность
Числовая последовательность Производные сложной и обратной функций
Производные сложной и обратной функций Лекция. Ряды
Лекция. Ряды Линейная алгебра. Матрицы
Линейная алгебра. Матрицы Решение уравнений
Решение уравнений Историческая задача
Историческая задача Функция. График функции
Функция. График функции Устный счёт на уроке математики в 1 классе
Устный счёт на уроке математики в 1 классе Задачи с экономическим содержанием
Задачи с экономическим содержанием Задачи на нахождение площади прямоугольника и трапеции
Задачи на нахождение площади прямоугольника и трапеции Линейные уравнения. Решение задач с помощью линейных уравнений. 7 класс
Линейные уравнения. Решение задач с помощью линейных уравнений. 7 класс Презентация на тему Смежные и вертикальные углы
Презентация на тему Смежные и вертикальные углы  Презентация на тему Центральная и осевая симметрии в природе
Презентация на тему Центральная и осевая симметрии в природе  Введение в общую алгебру
Введение в общую алгебру Задачи на прогрессию
Задачи на прогрессию Решение уравнений
Решение уравнений Реляционная алгебра
Реляционная алгебра Двоичная арифметика
Двоичная арифметика Арифметическая прогрессия в истории
Арифметическая прогрессия в истории Признаки параллельности прямых
Признаки параллельности прямых Отношения и пропорции. Игра Кот в мешке
Отношения и пропорции. Игра Кот в мешке