Треугольники (элементы, площади)

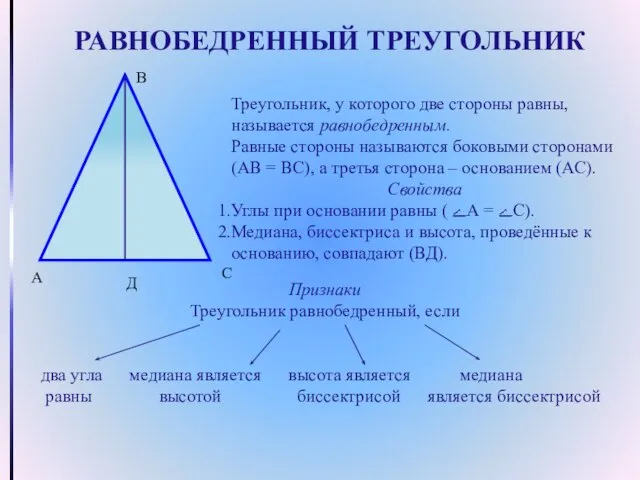
РАВНОБЕДРЕННЫЙ ТРЕУГОЛЬНИК
Треугольник, у которого две стороны равны, называется равнобедренным.
Равные стороны называются боковыми сторонами (АВ = ВС), а третья сторона – основанием (АС).
Свойства
Углы при основании равны ( ےА = ےС).
Медиана, биссектриса и высота, проведённые к основанию, совпадают (ВД).
В
А
С
Д
Признаки
Треугольник равнобедренный, если
два угла медиана является высота является медиана
равны высотой биссектрисой является биссектрисой

РАВНОСТОРОННИЙ ТРЕУГОЛЬНИК
Треугольник, у которого все стороны равны, называется равносторонним (правильным).
Свойства
Все углы равны ( ےА = ےВ = ےС).
Каждая медиана совпадает с биссектрисой и высотой, проведёнными из той же вершины (ВД).
Центры вписанной и описанной окружностей совпадают.
В
А
С
Д
О
r
R
а
ОД = r =
=
ОВ = R =
=
R = 2r
h =
S =
=
=
R =
r =

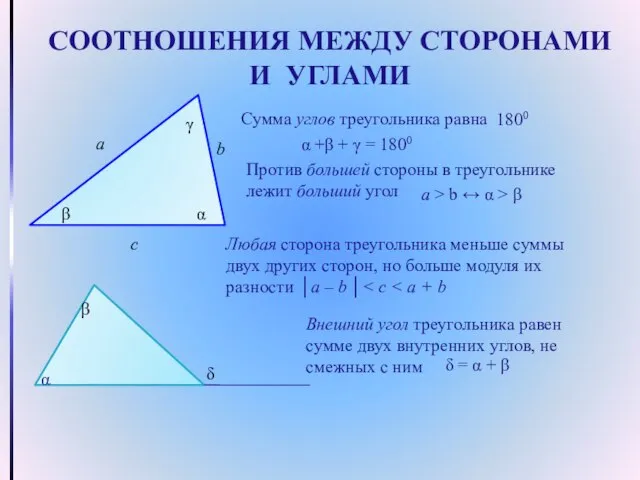
СООТНОШЕНИЯ МЕЖДУ СТОРОНАМИ И УГЛАМИ
Сумма углов треугольника равна
а
b
с
β
γ
1800
α
α +β + γ = 1800
Против большей стороны в треугольнике лежит больший угол
а > b ↔ α > β
Любая сторона треугольника меньше суммы двух других сторон, но больше модуля их разности │а – b │< c < a + b
α
β
δ
Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним
δ = α + β

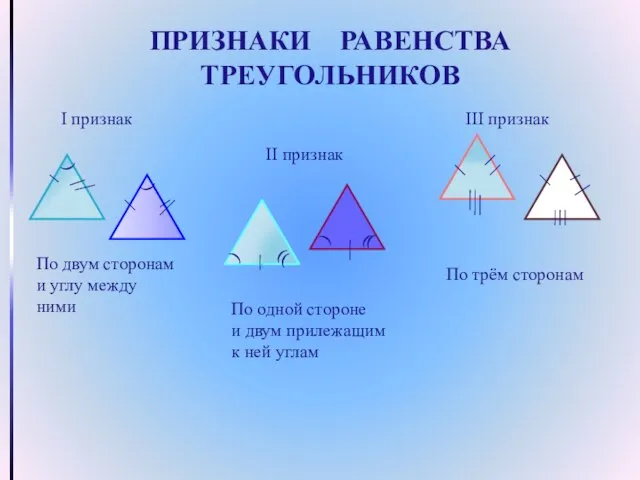
ПРИЗНАКИ РАВЕНСТВА ТРЕУГОЛЬНИКОВ
I признак
)
)
По двум сторонам и углу между ними
II признак
III признак
)
)
)
)
)
)
По одной стороне
и двум прилежащим
к ней углам
По трём сторонам

ПРИЗНАКИ ПОДОБИЯ ТРЕУГОЛЬНИКОВ
А
В
М
N
С
P
ΔАВС ∞ ΔMNP
1. ےА = ےМ ے В = ےN
2. ےA = ےM
3.

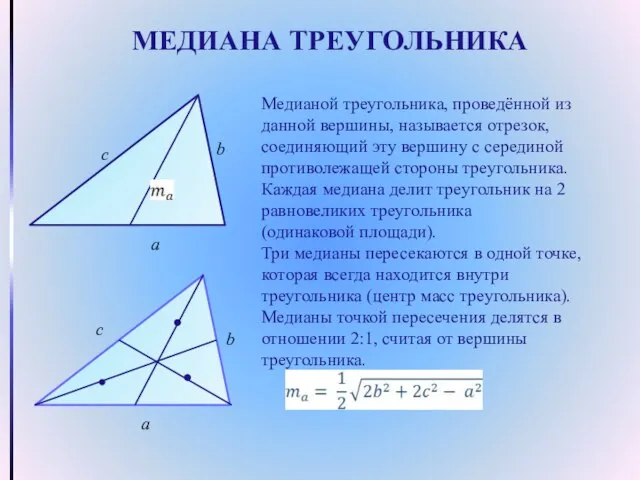
МЕДИАНА ТРЕУГОЛЬНИКА
Медианой треугольника, проведённой из данной вершины, называется отрезок, соединяющий эту вершину с серединой противолежащей стороны треугольника.
Каждая медиана делит треугольник на 2 равновеликих треугольника
(одинаковой площади).
Три медианы пересекаются в одной точке, которая всегда находится внутри треугольника (центр масс треугольника). Медианы точкой пересечения делятся в отношении 2:1, считая от вершины треугольника.
а
b
с
а
b
с

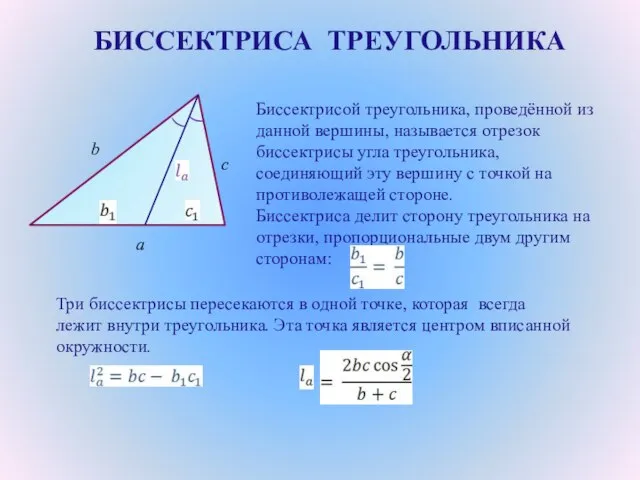
БИССЕКТРИСА ТРЕУГОЛЬНИКА
Биссектрисой треугольника, проведённой из данной вершины, называется отрезок биссектрисы угла треугольника, соединяющий эту вершину с точкой на противолежащей стороне.
Биссектриса делит сторону треугольника на отрезки, пропорциональные двум другим сторонам:
а
b
с
(
(
Три биссектрисы пересекаются в одной точке, которая всегда лежит внутри треугольника. Эта точка является центром вписанной окружности.

ВЫСОТА ТРЕУГОЛЬНИКА
Высотой треугольника, опущенной из данной вершины, называется перпендикуляр, проведённый из этой вершины к прямой , содержащей противолежащую сторону треугольника.
Прямые, содержащие высоты треугольника, пересекаются в одной точке. Эта точка называется ортоцентром.
а
b
с
Ортоцентр остроугольного треугольника лежит внутри треугольника. Ортоцентр прямоугольного треугольника совпадает с вершиной прямого угла. Ортоцентр тупоугольного треугольника лежит вне треугольника. Высоты треугольника обратно пропорциональны его сторонам:
¬
¬
¬

СРЕДНЯЯ ЛИНИЯ ТРЕУГОЛЬНИКА
Средняя линия параллельна одной из сторон треугольника и равна её половине:
MN ║AC , MN = AC.
Она отсекает треугольник, подобный данному, с коэффициентом подобия
В
А
С
M
N

ТЕОРЕМЫ КОСИНУСОВ И СИНУСОВ
Для произвольного треугольника, длины сторон которого обозначены a, b, c, а величины противолежащих им углов
а
b
с
β
γ
α
α, ,
β,
γ,
справедливы две теоремы.
Теорема косинусов:
Теорема синусов:
где R - радиус описанной окружности

ПЛОЩАДИ ТРЕУГОЛЬНИКА
Для произвольного треугольника, длины сторон которого обозначены a, b, c, а высота
а
b
с
¬
В
С
А
площади вычисляются по формулам:
S =
S =
β
S =
S =
, где r – радиус вписанной окружности
, где
S =
, где R – радиус описанной окружности
(формула Герона)
p =

ВПИСАННАЯ ОКРУЖНОСТЬ
а
b
О
r
c
В любой треугольник можно вписать окружность.
Центр вписанной окружности – точка пересечения биссектрис.
, где S площадь треугольника, а
p =
L
L
A
B
C
M
L
N
p-a
p-a
p-b
p-c
p-b
p-c