и другая прямая перпендикулярна к этой прямой.
Докажем лемму о перпендикулярности двух
параллельных прямых к третьей прямой
Лемма:
Доказательство:
Пусть a || b и a ⊥ b. Докажем, что b ⊥ c. Через произвольную т. М пространства, не лежащую на данных прямых, проведем прямые МА и МС, параллельные соответственно прямым a и c. Так как a ⊥ c, то AMC = 90°.
По условию b || а, а по построению а || МА, поэтому b || МА. Итак, прямые b и с параллельны соответственно прямым МА и МС, угол между которыми равен 90°. Это означает, что угол между прямыми b и с также равен 90°, т. е. b ⊥ c.
Рис. 2
b
a
C
A
M
c





 Умножение, деление, сложение и вычитание десятичных дробей
Умножение, деление, сложение и вычитание десятичных дробей Расчет центральной предельной теоремы
Расчет центральной предельной теоремы Теория вероятностей. Системы случайных величин
Теория вероятностей. Системы случайных величин Проценты
Проценты Математическое путешествие (1 урок)
Математическое путешествие (1 урок) Полулогарифмические модели
Полулогарифмические модели Занимательная математика
Занимательная математика Решение задач на кратное сравнение чисел
Решение задач на кратное сравнение чисел Первый признак равенства треугольников
Первый признак равенства треугольников Уменьшаемое. Вычитаемое. Разность
Уменьшаемое. Вычитаемое. Разность Погрешность результата измерения
Погрешность результата измерения Правильные многогранники. Моделирование многогранников
Правильные многогранники. Моделирование многогранников Свойства логарифмов
Свойства логарифмов Треугольники
Треугольники Степень с натуральным и целым показателем
Степень с натуральным и целым показателем Урок – творческий проект по математике Мастерская игрушек
Урок – творческий проект по математике Мастерская игрушек mik_tangram
mik_tangram Оценки параметров распределения. Статистические оценки
Оценки параметров распределения. Статистические оценки Число 10
Число 10 Тригонометрические функции острого угла прямоугольного треугольника. Решение прямоугольных треугольников
Тригонометрические функции острого угла прямоугольного треугольника. Решение прямоугольных треугольников Бесконечность величин
Бесконечность величин урок 1, урок 2 9кл геом водный урок
урок 1, урок 2 9кл геом водный урок Ситуация успеха на уроках математики как средство повышения качества образования
Ситуация успеха на уроках математики как средство повышения качества образования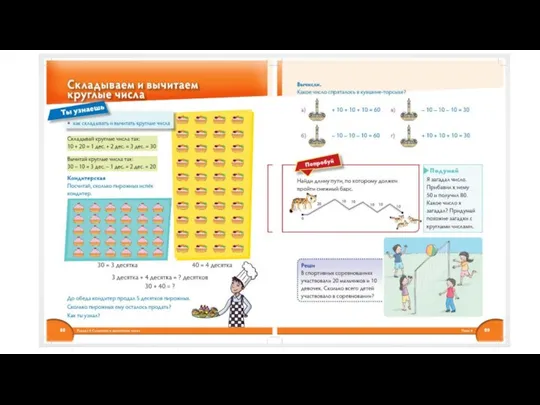 Складываем и вычитаем круглые числа. Грамота
Складываем и вычитаем круглые числа. Грамота Логарифмическая функция. Математика 11 класс
Логарифмическая функция. Математика 11 класс Задачи на увеличение и на уменьшение числа в несколько раз
Задачи на увеличение и на уменьшение числа в несколько раз Численное решение нелинейных уравнений (метод итераций, метод хорд, комбинированный метод)
Численное решение нелинейных уравнений (метод итераций, метод хорд, комбинированный метод) Презентация на тему Степень с целым показателем
Презентация на тему Степень с целым показателем