Содержание
- 3. ПЛОЩАДИ Не для школы, а для жизни мы учимся. Античный афоризм
- 16. ЗАДАЧА История сохранила легенду о следующей самой древней экстремальной задаче, известной как задача Дидоны. Финикийская царевна
- 17. Воины Дидоны разрезали шкуру на тонкие полоски, и Дидона охватила ремнем, составленным из этих полосок, участок
- 18. В геометрии эта задача звучит так: «Какие геометрические фигуры с одинаковым периметром имеют наибольшую площадь?»
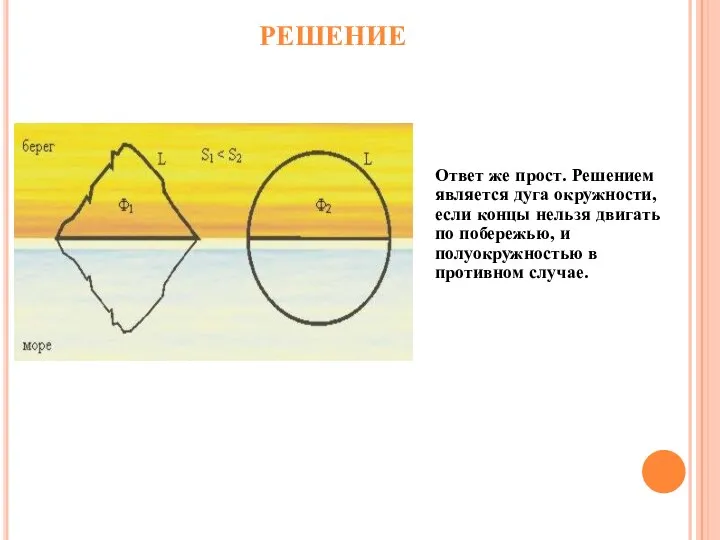
- 19. РЕШЕНИЕ Ответ же прост. Решением является дуга окружности, если концы нельзя двигать по побережью, и полуокружностью
- 20. В кабинете математики решили покрыть пол паркетной доской в виде квадрата со стороной 20 см. Длина
- 21. ЗАДАЧА Пенсионерка купила заборчик длиной 7 метров для клумбы. Она спрашивает, какой формы ей лучше сделать
- 22. ЗАДАЧА Решение: Ответ: круг имеет наибольшую площадь.
- 24. Скачать презентацию








 Ортодромия и локсодромия
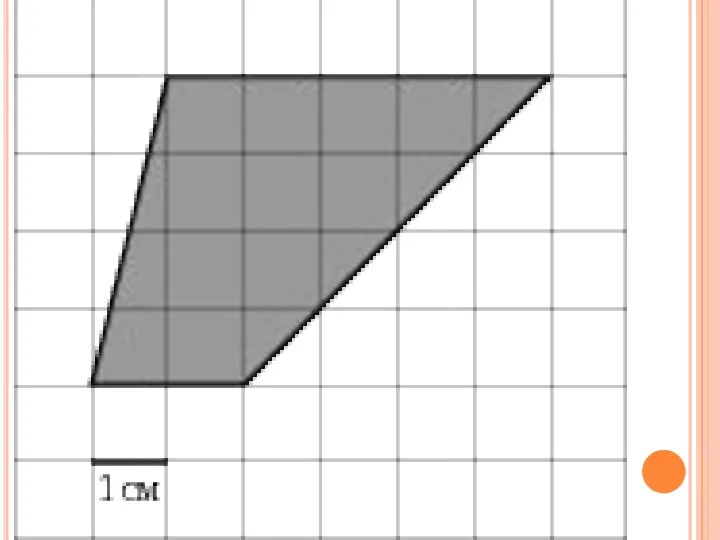
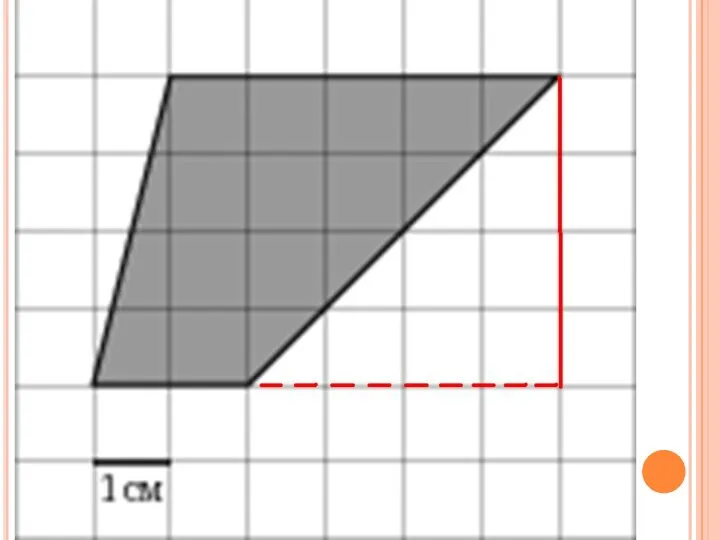
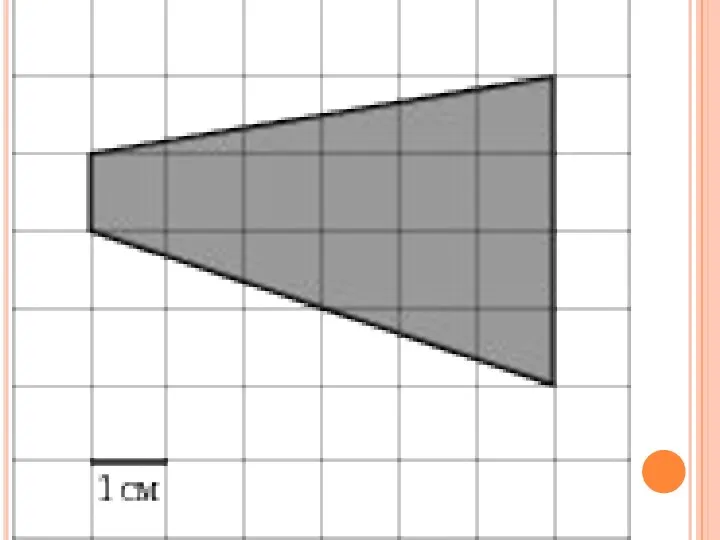
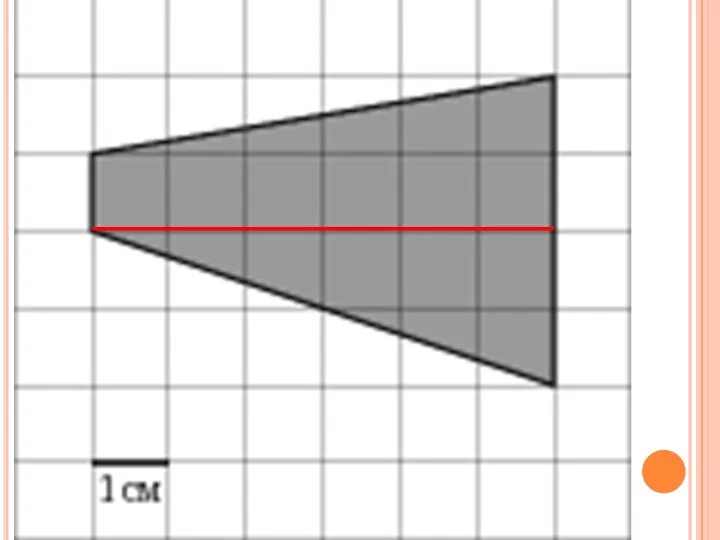
Ортодромия и локсодромия Трапеция
Трапеция Основы теории оболочек вращения
Основы теории оболочек вращения Презентация на тему Решение задач - Треугольники
Презентация на тему Решение задач - Треугольники  Введение понятия целого и дробного выражения
Введение понятия целого и дробного выражения График функции. Урок применения знаний и умений. Класс: 8
График функции. Урок применения знаний и умений. Класс: 8 Объем прямоугольного параллелепипеда
Объем прямоугольного параллелепипеда Временные ряды
Временные ряды Первый урок математики в 6 классе. Начинается новый учебный год
Первый урок математики в 6 классе. Начинается новый учебный год Решение уравнений (урок 3). 6 класс
Решение уравнений (урок 3). 6 класс SW1 Product Manual Product Feature | Q&A
SW1 Product Manual Product Feature | Q&A Презентация на тему Цилиндр 11 класс
Презентация на тему Цилиндр 11 класс  Работа в тетради
Работа в тетради Логическая задача со спичками
Логическая задача со спичками Основные понятия теории множеств, комбинаторики, теории вероятности
Основные понятия теории множеств, комбинаторики, теории вероятности «Числа от 1 до 1000»
«Числа от 1 до 1000» Задача о баскетболисте. Расчетная работа №1
Задача о баскетболисте. Расчетная работа №1 Решение систем неравенств
Решение систем неравенств Системы линейных уравнений
Системы линейных уравнений Логарифмические уравнения и неравенства. Практическая работа
Логарифмические уравнения и неравенства. Практическая работа Экстремум функции двух переменных. Задания
Экстремум функции двух переменных. Задания Правила выполнения действий с натуральными числами
Правила выполнения действий с натуральными числами Вычисление углов между двумя прямыми, между прямой и плоскостью
Вычисление углов между двумя прямыми, между прямой и плоскостью Согласные звуки [в],[ в’], буквы В, в
Согласные звуки [в],[ в’], буквы В, в Построение треугольника по трем сторонам
Построение треугольника по трем сторонам Формирование функциональной грамотности школьников на уроках математики через решение нестандартных задач
Формирование функциональной грамотности школьников на уроках математики через решение нестандартных задач Подготовка к итоговой контрольной работе (11 класс)
Подготовка к итоговой контрольной работе (11 класс) Определение логарифма
Определение логарифма