Четыре замечательные точки треугольника

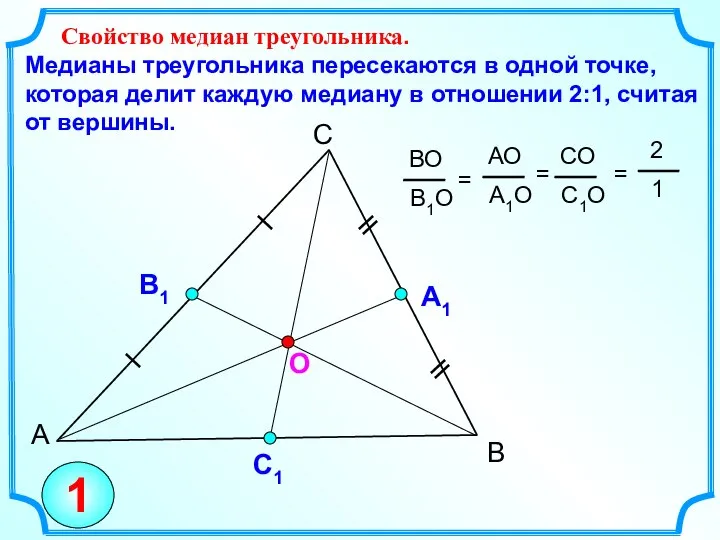
А
С
В
Свойство медиан треугольника.
Медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2:1, считая от вершины.
В1
А1
О
СО
С1О
=
С1
1

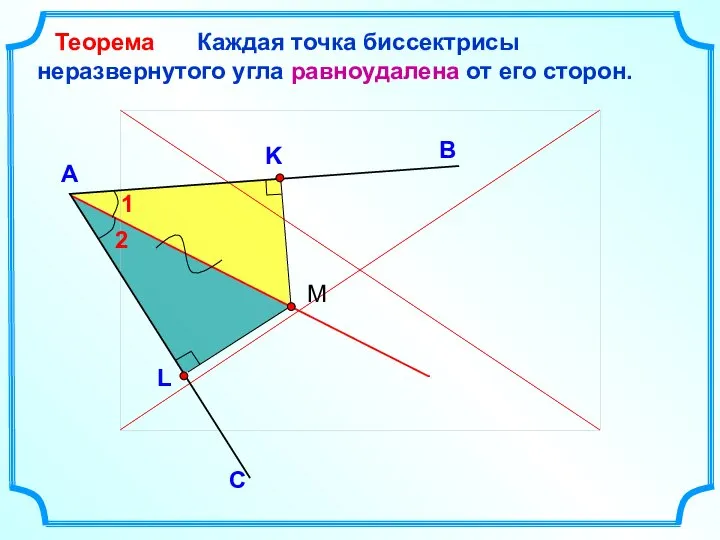
Каждая точка биссектрисы неразвернутого угла равноудалена от его сторон.
В
А
Теорема
С

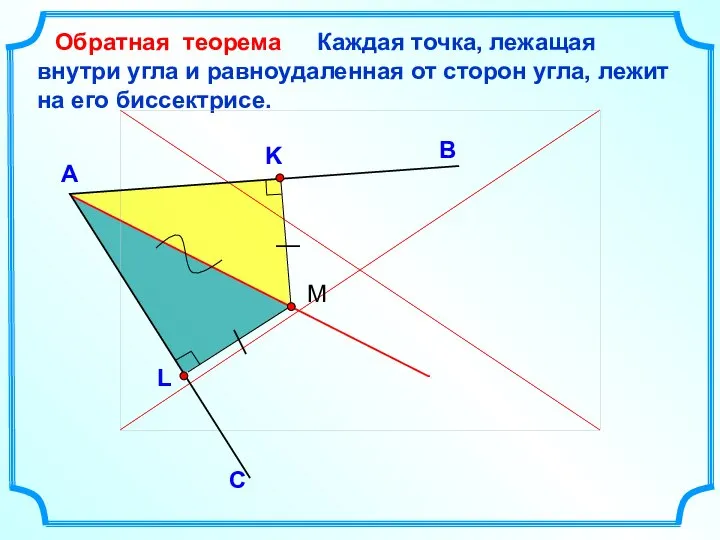
Каждая точка, лежащая внутри угла и равноудаленная от сторон угла, лежит на его биссектрисе.
В
А
Обратная теорема
С

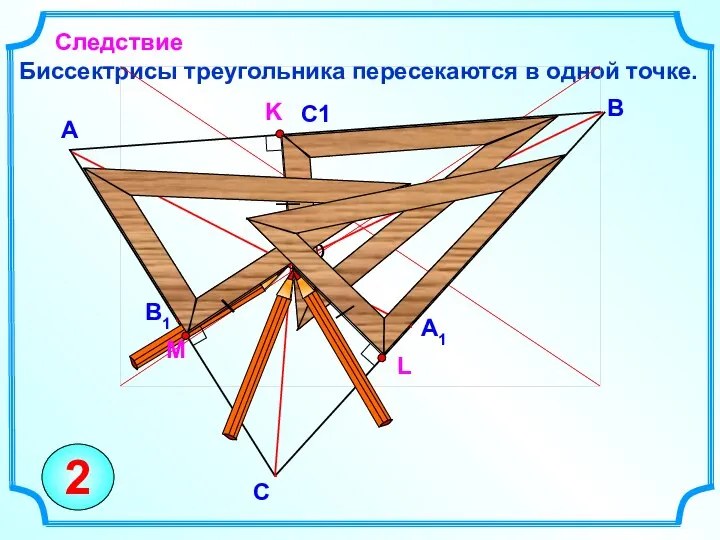
Биссектрисы треугольника пересекаются в одной точке.
В
А
Следствие
С
2

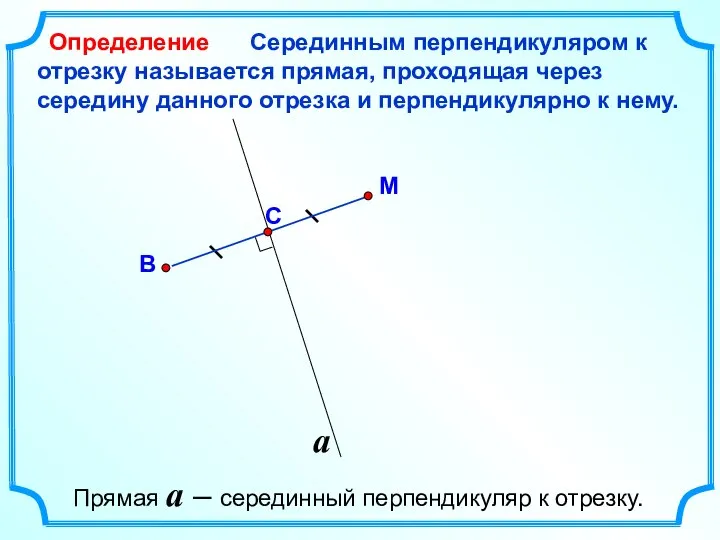
Серединным перпендикуляром к отрезку называется прямая, проходящая через середину данного отрезка и перпендикулярно к нему.
М
В
Определение
Прямая a – серединный перпендикуляр к отрезку.

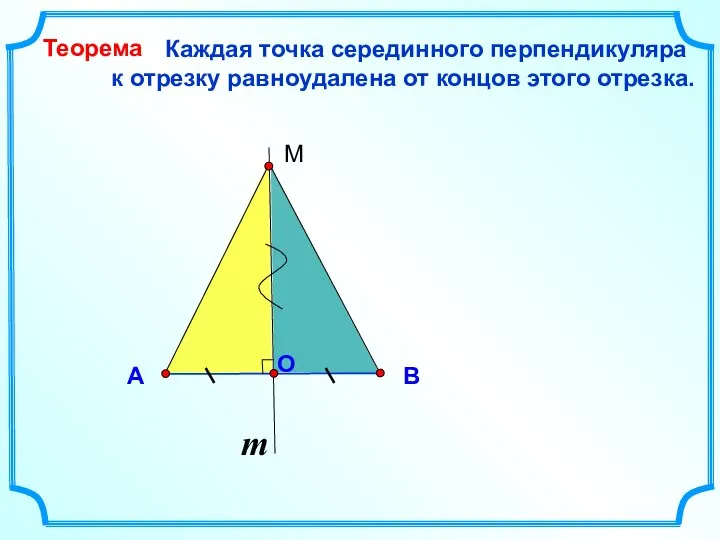
Каждая точка серединного перпендикуляра
к отрезку равноудалена от концов этого отрезка.
B
A
Теорема

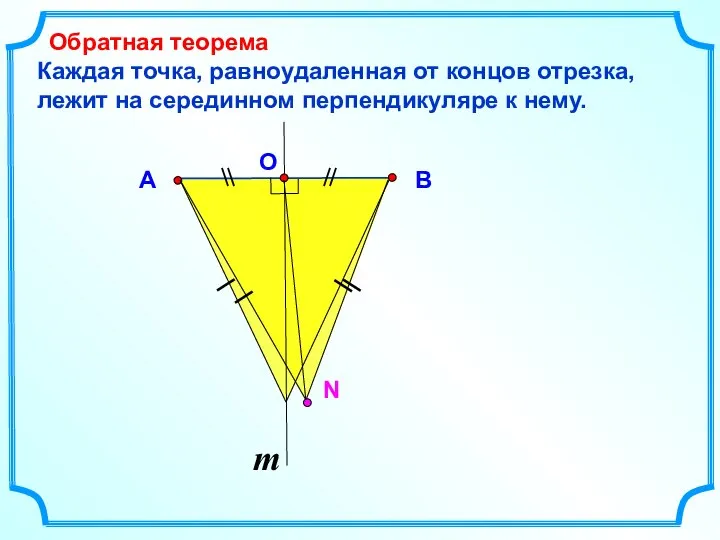
Каждая точка, равноудаленная от концов отрезка, лежит на серединном перпендикуляре к нему.
Обратная теорема

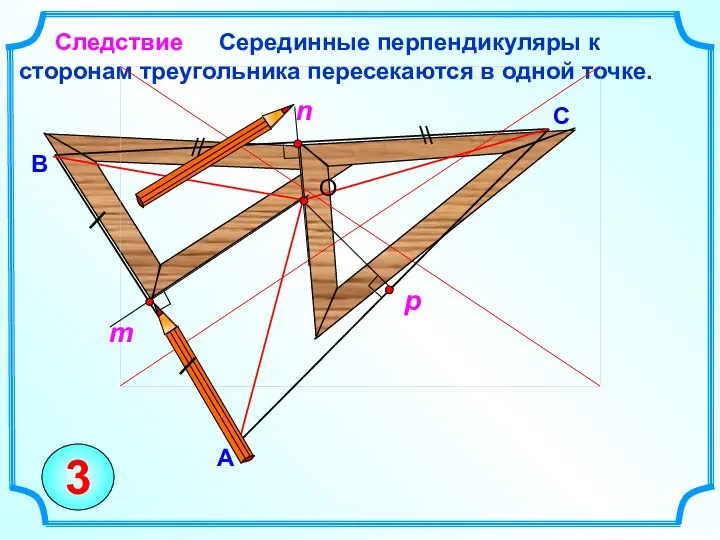
Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.
C
B
Следствие
A
3

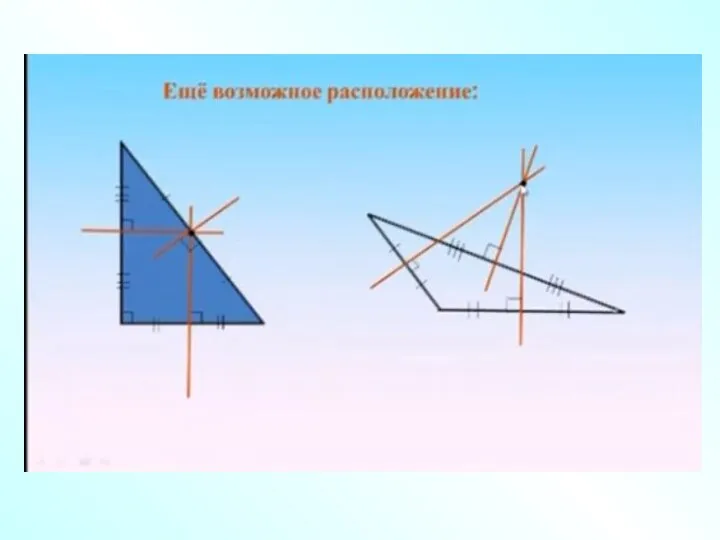
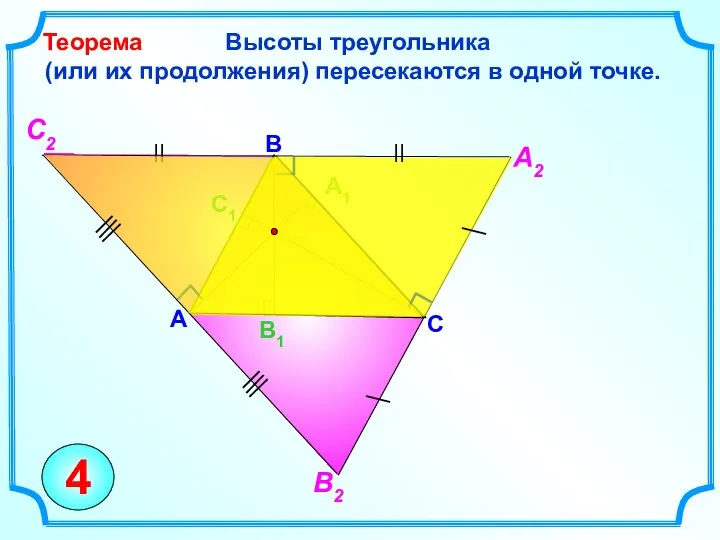
Высоты треугольника
(или их продолжения) пересекаются в одной точке.
Теорема
C
B
A
4

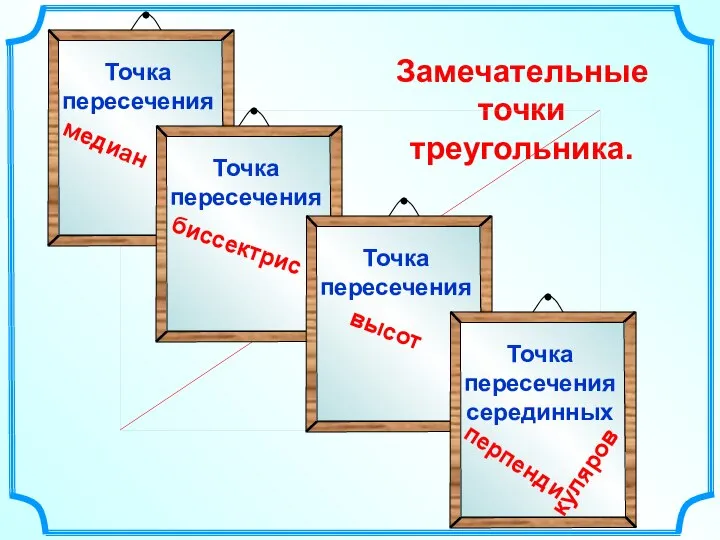
Замечательные точки треугольника.

Треугольник, который опирается на острие иглы в точке пересечения медиан, находится в равновесии!
Точка, обладающая таким свойством, называется
центром тяжести треугольника.

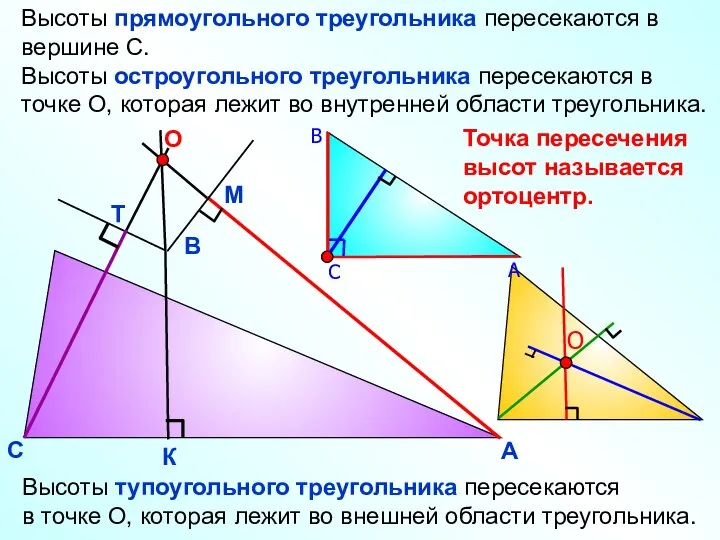
А
В
С
К
М
Т
Высоты тупоугольного треугольника пересекаются
в точке О, которая лежит во внешней области треугольника.
Высоты прямоугольного треугольника пересекаются в вершине С.
Высоты остроугольного треугольника пересекаются в точке О, которая лежит во внутренней области треугольника.
А
В
С
Точка пересечения
высот называется
ортоцентр.

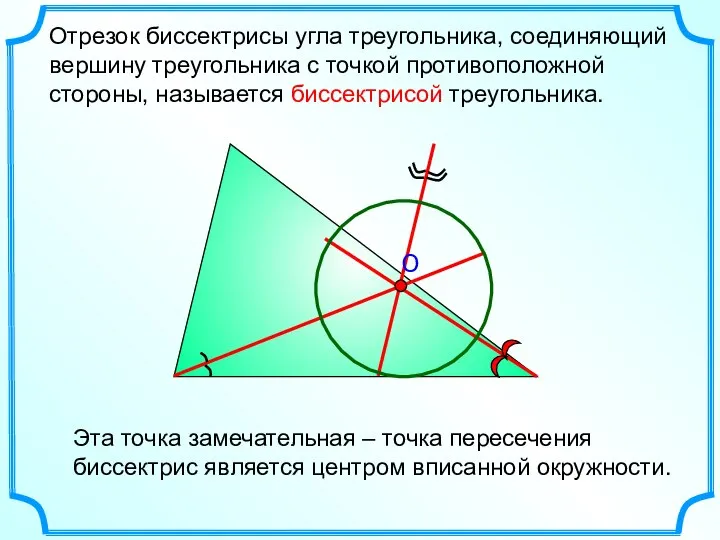
Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны, называется биссектрисой треугольника.
Эта точка замечательная – точка пересечения биссектрис является центром вписанной окружности.