Цилиндр в математике

Что такое цилиндр?
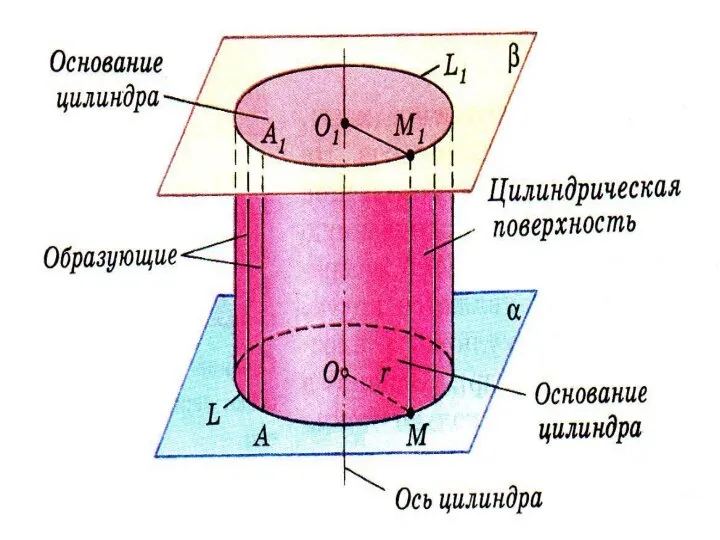
Цилиндр (круговой цилиндр) – тело, которое состоит из двух кругов, совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих кругов. Круги называются основаниями цилиндра, а отрезки, соединяющие соответствующие точки окружностей кругов, – образующими цилиндра

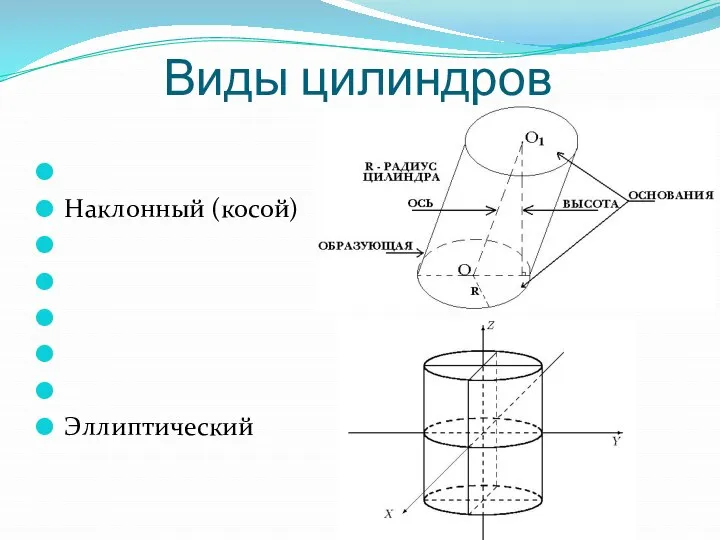
Виды цилиндров
Наклонный (косой)
Эллиптический

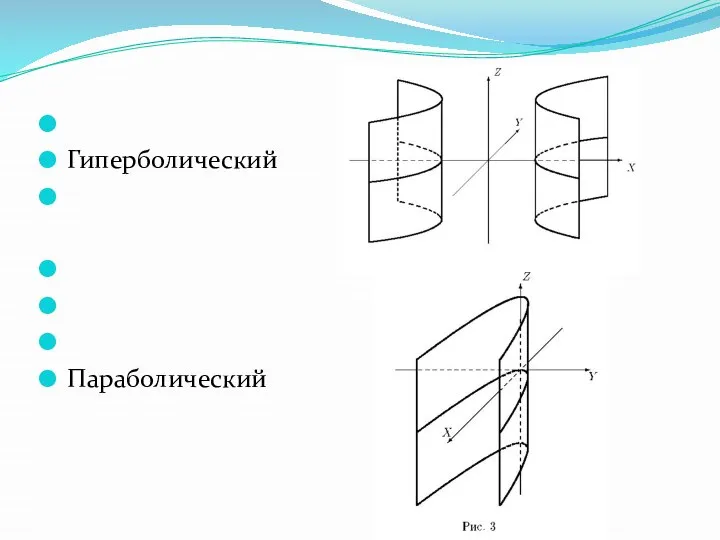
Гиперболический
Параболический

Площадь цилиндра (прямой круговой)
Площадь боковой поверхности цилиндра можно вычислить, умножив длину образующей на периметр сечения цилиндра плоскостью, перпендикулярной образующей (основание).
Sb = Ph
P = 2πR ? Sb = 2πRh.
Площадь полной поверхности цилиндра равна сумме площадей его боковой поверхности и его оснований.
Sp = 2πRh + 2πR2 = 2πR(h + R)

Площадь цилиндра (наклонный круговой)
Для расчета площади боковой поверхности наклонного цилиндра потребуется перемножить значения образующей и периметра сечения, которое будет перпендикулярно выбранной образующей.
Sбок= х Р,
где х — длина образующей цилиндра, Р — периметр сечения.
Сечение, кстати, лучше выбирать такое, чтобы оно образовывало эллипс. Тогда будут упрощены расчеты его периметра. Длина эллипса вычисляется по формуле, которая дает приблизительный ответ.
l = π (а + в),
где «а» и «в» — полуоси эллипса, то есть расстояния от центра до ближайшей и самой дальней его точек.
Площадь всей поверхности нужно вычислять с помощью такого выражения:
Sпол = 2 π r^2 + х Р

Объём цилиндра (прямой круговой)
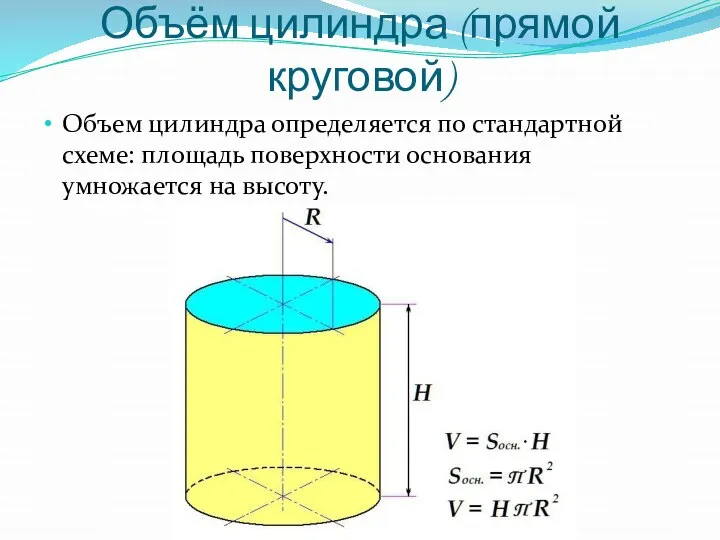
Объем цилиндра определяется по стандартной схеме: площадь поверхности основания умножается на высоту.

Объём цилиндра (наклонный круговой)
Площадь поверхности основания умножают на расстояние между плоскостями – перпендикулярный отрезок, построенный между ними. Как видно из рисунка, такой отрезок равен произведению длины образующей на синус угла наклона образующей к плоскости.

Скошенный цилиндр
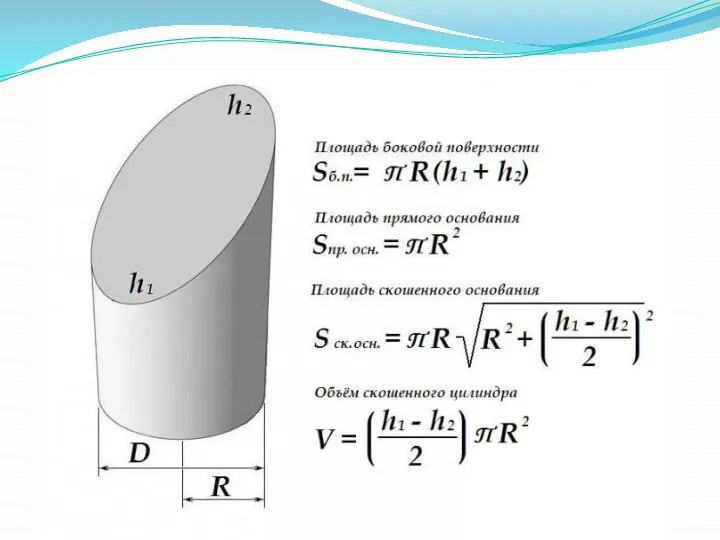
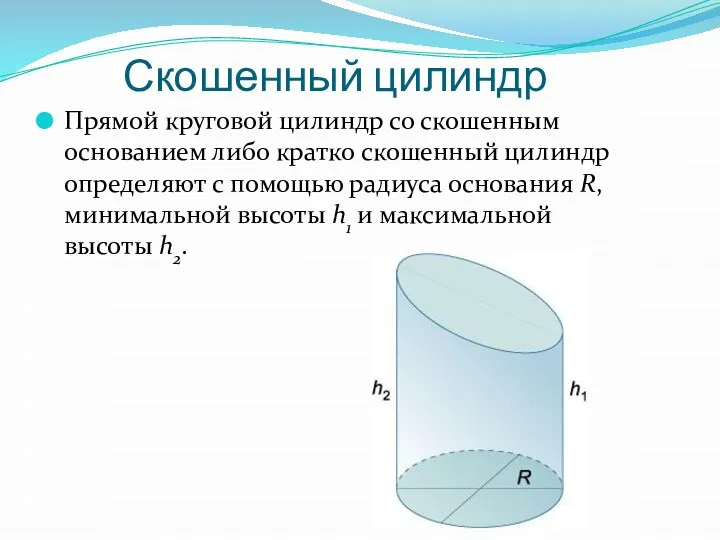
Прямой круговой цилиндр со скошенным основанием либо кратко скошенный цилиндр определяют с помощью радиуса основания R, минимальной высоты h1 и максимальной высоты h2.