Содержание
- 2. Значение переменной, при котором каждое из неравенств системы обращается в верное числовое неравенство, называют частным решением
- 3. Решить систему неравенств – значит найти все её частные решения, либо доказать , что у данной
- 4. Решение системы неравенств – это пересечение решений неравенств, входящих в систему. Запомните! Решение системы неравенств –
- 5. Алгоритм решения системы неравенств с одной переменной: 1. отдельно решить каждое неравенство; 2. найти пересечение найденных
- 6. Пример 1. Решить систему неравенств Решение. Отметим эти промежутки на координатной прямой. Решение первого неравенства помечено
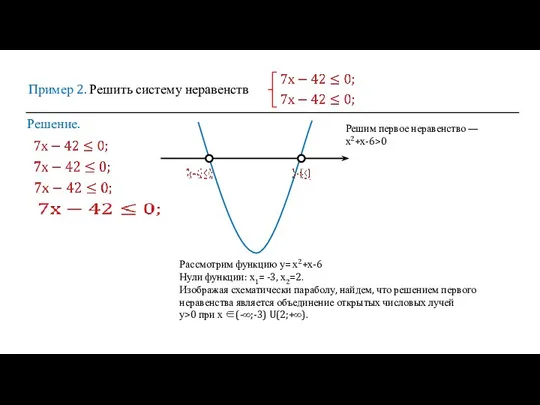
- 7. Пример 2. Решить систему неравенств Решение. Решим первое неравенство — х2+х-6>0 Рассмотрим функцию у= х2+х-6 Нули
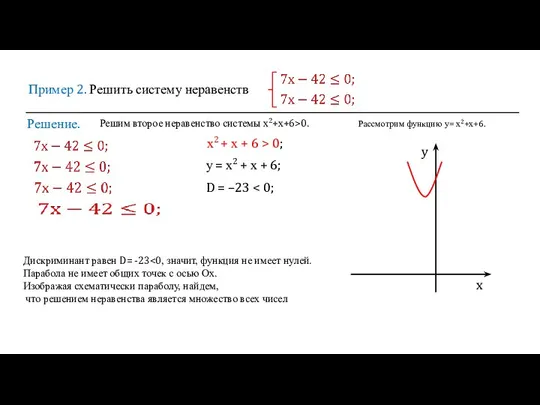
- 8. Пример 2. Решить систему неравенств Решение. х2 + х + 6 > 0; у = х2
- 9. Пример 2. Решить систему неравенств Решение. х2 + х + 6 > 0; у = х2
- 10. Говорят, что несколько неравенств с одной переменной образуют совокупность неравенств, если ставится задача найти все такие
- 11. Каждое такое значение переменной называют частным решением совокупности неравенств.
- 12. Множество всех частных решений совокупности неравенств представляет собой общее решение совокупности неравенств. Запомните! Решение совокупности неравенств
- 13. Алгоритм решения совокупности неравенств: 1. отдельно решить каждое неравенство; 2. найти объединение найденных решений. Это объединение
- 14. Пример 4. Решить совокупность неравенств Решение. Решение Преобразуем каждое из неравенств. Получим равносильную совокупность неравенств Для
- 15. Пример 5. Решить совокупность неравенств Решение. (2; +∞); Ответ: (2; +∞). Преобразуем каждое из неравенств. Получим
- 16. Решение неравенств с одной переменной. Иррациональные неравенства. Неравенства с модулем
- 17. Рассмотрим решение неравенства
- 18. 1. ОДЗ: f(х) ≥ 0; 2. g(х) > 0. При g(х) ≤ 0 неравенство не имеет
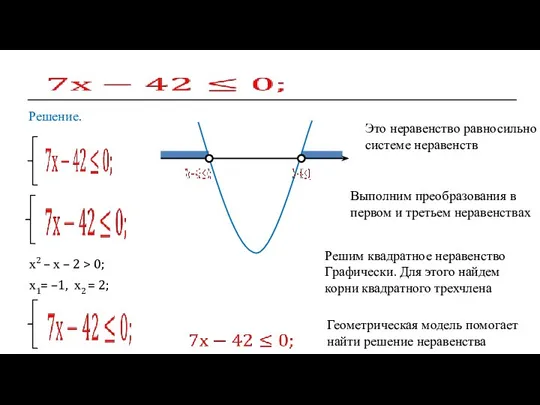
- 19. Решение. х2 – х – 2 > 0; х1= –1, х2 = 2; Это неравенство равносильно
- 20. Решение. х1= –2, х2 = 7; Это неравенство равносильно системе неравенств Выполним преобразования в каждом неравенстве
- 21. 3.
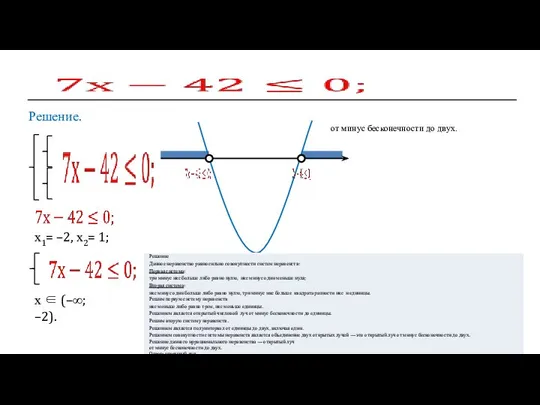
- 22. Решение. х ∈ (–∞; –2). х1= –2, х2= 1; от минус бесконечности до двух.
- 23. Решение. х ∈ (2; +∞); х ∈ (–∞; –2); х1= –2, х2= 1; Данное неравенство равносильно
- 24. Решение систем уравнений второй степени
- 25. Рассмотрим сначала системы уравнений с двумя переменными, составленные из одного уравнения второй степени и одного уравнения
- 26. Для этого выполняют следующий алгоритм действий: — выражают из уравнения первой степени одну переменную через другую;
- 27. Пример 1: Решить систему уравнений Решение: Ответ: (-1, 25; 0,75); (1,6; -0,2) Выразим из второго уравнения
- 28. Если система состоит из двух уравнений второй степени с двумя переменными, то найти её решения обычно
- 29. Пример 2: Решить систему уравнений Решение: Ответ: (-2; -1); (2; 1) x ≠ 0
- 30. Системы уравнений
- 31. Метод подстановки; метод алгебраического сложения; метод введения новых переменных; графический метод. Для решения систем уравнений с
- 32. Если поставлена задача – найти такие пары (х; у), которые одновременно удовлетворяют уравнению р(х; у) =
- 33. Пару значений (х; у), которая одновременно является решением и первого и второго уравнения системы, называют решением
- 34. Решить систему уравнений – значит найти все её решения или установить, что решений нет.
- 35. р(х; у; z) =0 q(х; у; z) =0 r(х; у; z) =0 Система трех уравнений с
- 36. Алгоритм решения системы уравнений постепенный переход от сложного уравнения к более простому, но при этом выполнять
- 37. Две системы уравнений называют равносильными, если они имеют одни и те же решения или решений не
- 38. метод подстановки; метод алгебраического сложения; введения новых переменных. Равносильные способы решения систем уравнений:
- 39. возведение в квадрат обеих частей уравнения; умножение уравнений системы; преобразования, приводящие к расширению области определения. Проверка
- 40. Пример 1. Решить систему уравнений х + у + 2z = 4, 2х + у +
- 41. Пример 2. Решить систему уравнений Решение. (1; 1), (–1; –1);
- 42. Задание 3 Решить систему уравнений: игрек квадрат плюс два икс игрек минус три икс квадрат равно
- 43. Пример 3. Решить систему уравнений Решение. Ответ: (1; 0). (1; 0), (–2; 3); х = –2,
- 45. Скачать презентацию





































 Математические ребусы. 2 класс
Математические ребусы. 2 класс Аксонометрические проекции
Аксонометрические проекции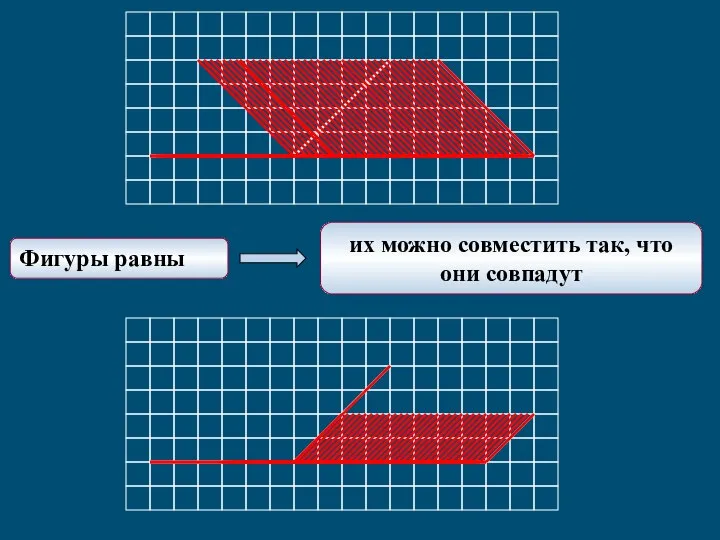 Равенство углов наложением
Равенство углов наложением Старинные меры длины на Руси
Старинные меры длины на Руси Площадь и объём фигуры
Площадь и объём фигуры Площадь многоугольника
Площадь многоугольника Теорема о трех перпендикулярах
Теорема о трех перпендикулярах Критерий Стьюдента
Критерий Стьюдента Состав чисел в пределах 10. Урок №80
Состав чисел в пределах 10. Урок №80 Приемы решения целых уравнений
Приемы решения целых уравнений 20f
20f Урок-игра Следствие ведут знатоки
Урок-игра Следствие ведут знатоки Обработка экспериментальных данных. Лекция 6: Регрессионный и корреляционный анализ. Нелинейная зависимость
Обработка экспериментальных данных. Лекция 6: Регрессионный и корреляционный анализ. Нелинейная зависимость Устная работа. Вычисления
Устная работа. Вычисления Правило округлення натуральних чисел і десяткових дробів
Правило округлення натуральних чисел і десяткових дробів Многочлен. Основные понятия. Определение многочлена
Многочлен. Основные понятия. Определение многочлена Четырехугольник . Прямоугольник. Квадрат
Четырехугольник . Прямоугольник. Квадрат Векторы на плоскости
Векторы на плоскости Скалярное произведение векторов. Задачи
Скалярное произведение векторов. Задачи Презентация на тему История возникновения интеграла
Презентация на тему История возникновения интеграла  Формула Пика
Формула Пика Прописываем число 13. Измеряем и сравниваем
Прописываем число 13. Измеряем и сравниваем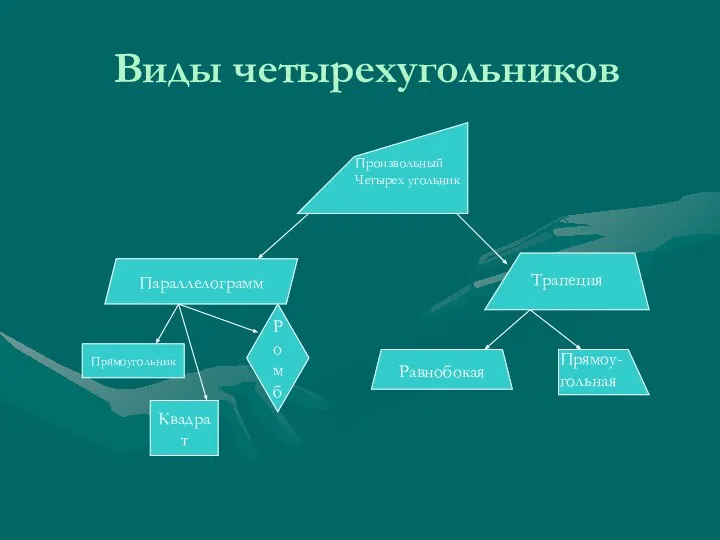 Виды четырехугольников
Виды четырехугольников Предмет математика. Счёт предметов. Один, два, три…
Предмет математика. Счёт предметов. Один, два, три… Приведите примеры элементарных исследований свойств при изучении первых функций
Приведите примеры элементарных исследований свойств при изучении первых функций Zaokrugljivanje decimalnih brojeva
Zaokrugljivanje decimalnih brojeva Средние величины и показатели вариации
Средние величины и показатели вариации Углы, связанные с окружностью
Углы, связанные с окружностью