Уравнения и неравенства с двумя переменными

Актуализация знаний

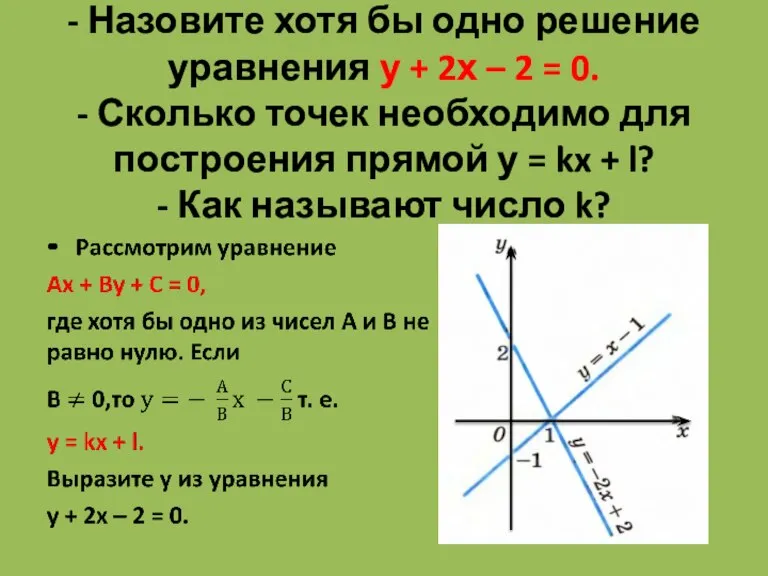
- Назовите хотя бы одно решение уравнения у + 2х – 2 = 0.
- Сколько точек необходимо для построения прямой у = kx + l?
- Как называют число k?

Линейные неравенства с двумя переменными.
Неравенства вида
Ах + Ву + С > 0 и
Ах + Ву + С < 0 называются строгими.
Неравенство с двумя неизвестными F(x,y)>0 имеет своими решениями пары чисел (х, у), которые изображаются точками плоскости.
Найти множество всех решений данного неравенства – это значит указать на плоскости множество точек, в которых это неравенство удовлетворяется.

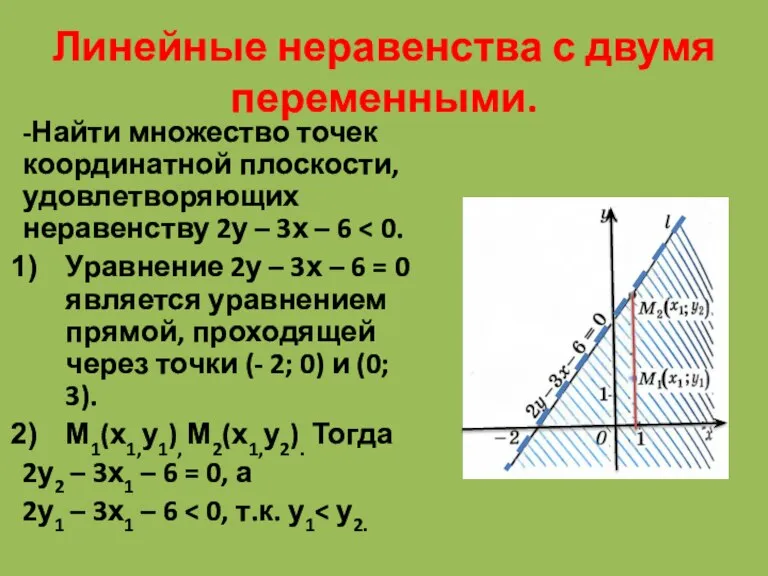
Линейные неравенства с двумя переменными.
-Найти множество точек координатной плоскости, удовлетворяющих неравенству 2у – 3х – 6 < 0.
Уравнение 2у – 3х – 6 = 0 является уравнением прямой, проходящей через точки (- 2; 0) и (0; 3).
М1(х1,у1), М2(х1,у2). Тогда
2у2 – 3х1 – 6 = 0, а
2у1 – 3х1 – 6 < 0, т.к. у1< у2.

Линейные неравенства с двумя переменными.

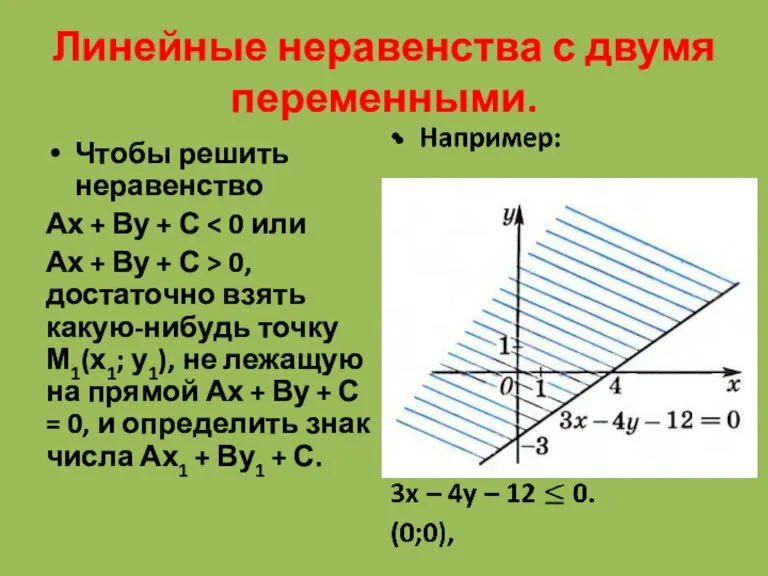
Линейные неравенства с двумя переменными.
Чтобы решить неравенство
Ах + Ву + С < 0 или
Ах + Ву + С > 0, достаточно взять какую-нибудь точку М1(х1; у1), не лежащую на прямой Ах + Ву + С = 0, и определить знак числа Ах1 + Ву1 + С.

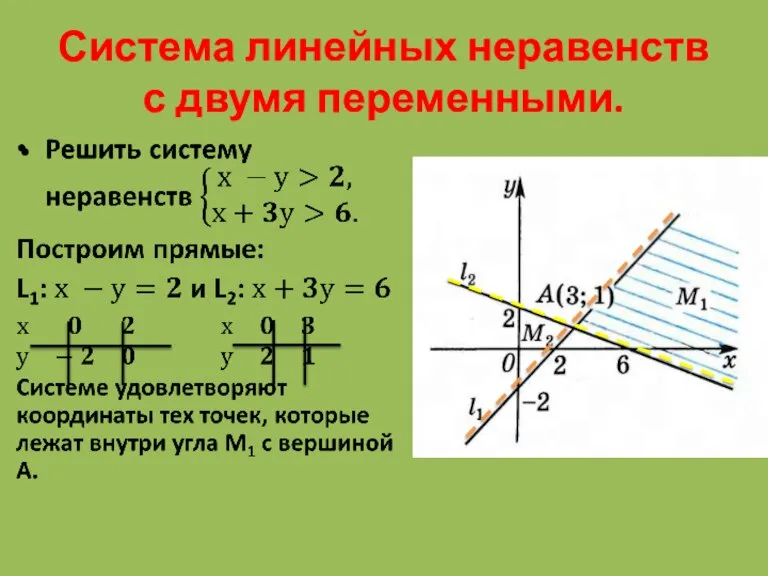
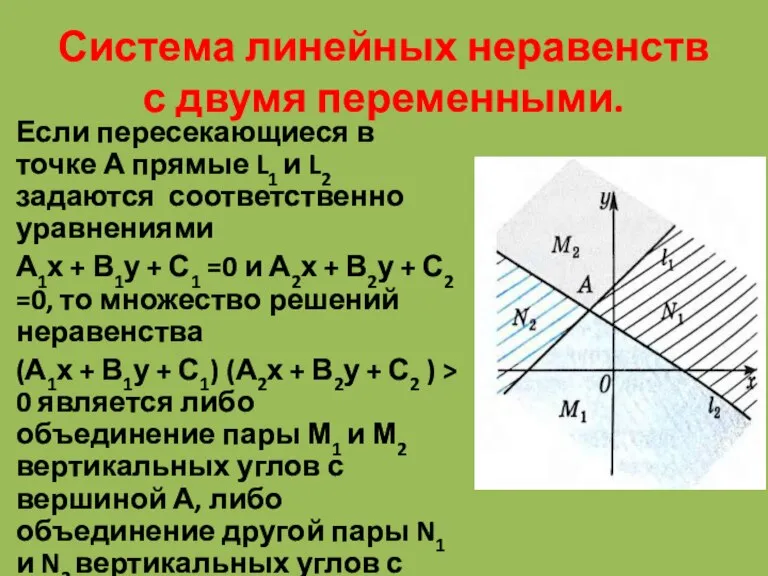
Система линейных неравенств с двумя переменными.

Система линейных неравенств с двумя переменными.
Если пересекающиеся в точке А прямые L1 и L2 задаются соответственно уравнениями
А1х + В1у + С1 =0 и А2х + В2у + С2 =0, то множество решений неравенства
(А1х + В1у + С1) (А2х + В2у + С2 ) > 0 является либо объединение пары М1 и М2 вертикальных углов с вершиной А, либо объединение другой пары N1 и N2 вертикальных углов с той же вершиной.

Система линейных неравенств с двумя переменными.
№1.
Найти множество точек координатной плоскости, удовлетворяющих неравенству
Зу – 2х + 4 < 0.