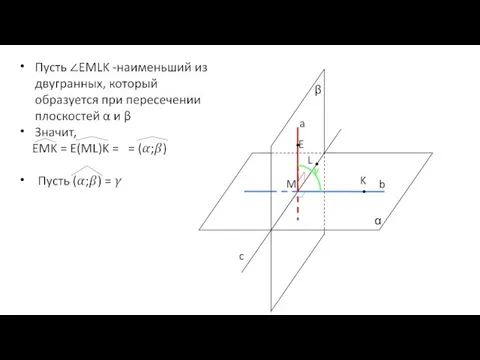
Слайд 2Пусть плоскости α и β пересекаются по прямой c.
α
β
c

Слайд 3В плоскости α проведем прямую b так, чтобы b c.
Пусть b∩c =

Слайд 4α
a
b
β
c
M
В плоскости β, через точку М проведем прямую а так, чтобы а

с.
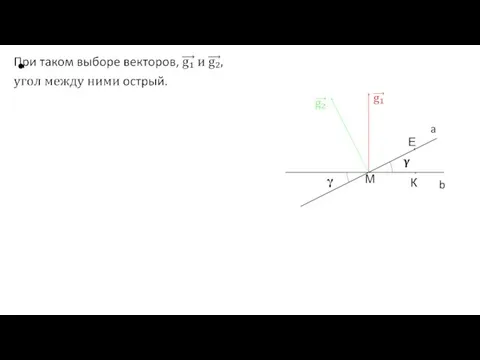
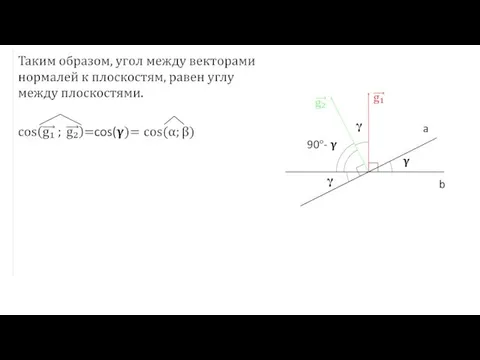
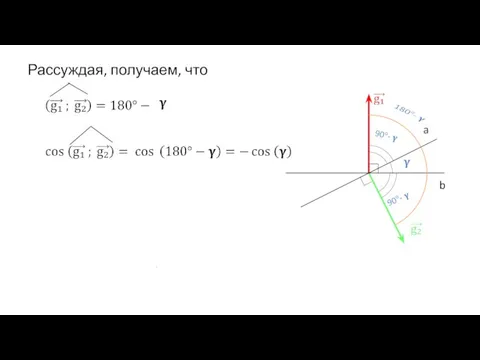
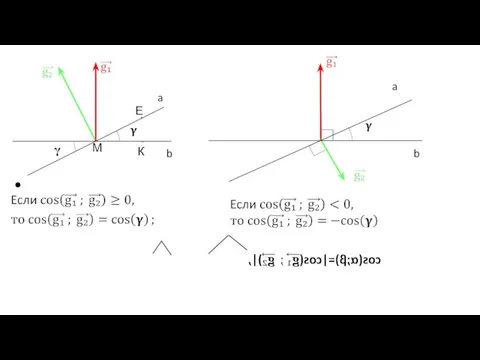
Слайд 10Но, векторы нормалей к плоскостям можно задать и так, что угол между
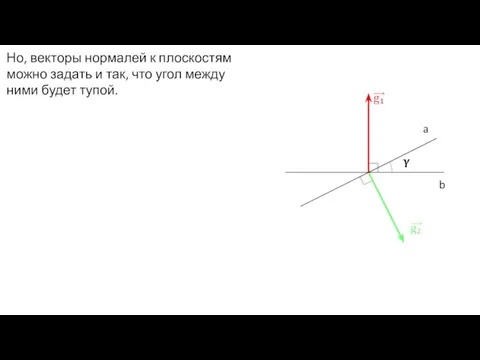
ними будет тупой.
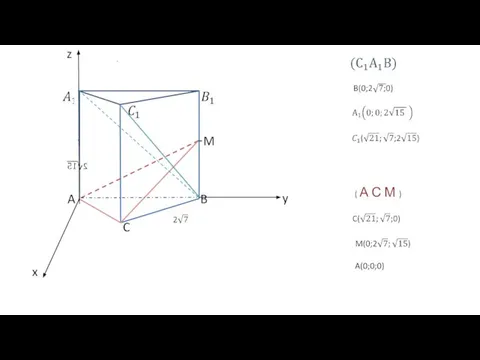
Слайд 14Практика использования выведенной формулы нахождения угла между плоскостями

Слайд 18
Записав скалярные произведения векторов через координаты этих векторов и выполнив некоторые преобразования,

получим следующую систему:
Слайд 19
Ax+By+Cz+D=0( каноническое уравнение плоскости)













 Презентация на тему Игра по математике "Счастливый случай"
Презентация на тему Игра по математике "Счастливый случай"  Сложение дробей
Сложение дробей Пифагор и его теорема
Пифагор и его теорема Скалярное произведение векторов
Скалярное произведение векторов Учебно – методическое обеспечение образовательного процесса по учебному предмету Математика в 2017/2018 учебном году
Учебно – методическое обеспечение образовательного процесса по учебному предмету Математика в 2017/2018 учебном году Применение графов
Применение графов Элементы аналитической геометрии. Векторы
Элементы аналитической геометрии. Векторы Устный счёт. Закрепление изученного
Устный счёт. Закрепление изученного Морской бой
Морской бой Перпендикулярность прямой и плоскости
Перпендикулярность прямой и плоскости Циліндр. Елементи циліндра
Циліндр. Елементи циліндра Игра
Игра Педагогическая диагностика как одно из средств изучения уровня математической подготовки учащихся
Педагогическая диагностика как одно из средств изучения уровня математической подготовки учащихся Л 8 Предел функции
Л 8 Предел функции Формулы для радиусов вписанной и описанной окружностей треугольника
Формулы для радиусов вписанной и описанной окружностей треугольника Производная и исследование функции
Производная и исследование функции Технология подготовки учащихся к овладению решения задач с параметрами комбинированными методами. Занятие №5
Технология подготовки учащихся к овладению решения задач с параметрами комбинированными методами. Занятие №5 Угол. Виды углов. Опрос
Угол. Виды углов. Опрос Применение векторов к решению задач
Применение векторов к решению задач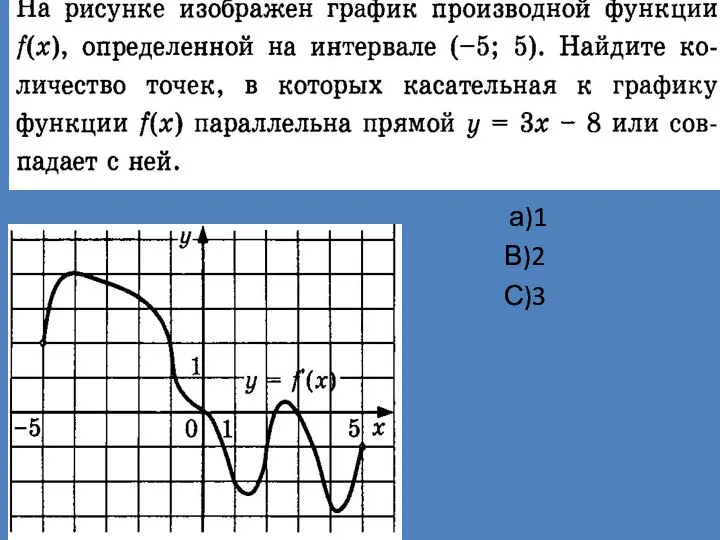 График производной функции
График производной функции Решаем задачи
Решаем задачи Устный счёт. 3 класс
Устный счёт. 3 класс Многогранники (задания)
Многогранники (задания) Решение задач при помощи уравнений
Решение задач при помощи уравнений Отрицательные числа в географии
Отрицательные числа в географии Признаки существования предела
Признаки существования предела Конкурс капитанов
Конкурс капитанов Взаимно обратные числа
Взаимно обратные числа