Векторы в пространстве

Какие величины характеризуются не только числом, но еще и направлением?
Скорость
Ускорение
Сила
Такие величины называются векторными величинами или просто векторами.

Что такое вектор?
Отрезок, для которого указано, какой из его концов считается началом, а какой – концом, называется вектором.
Вектор характеризуется следующими элементами:
1) начальной точкой;
2) направлением;
3) длиной.
Геометрически векторы
изображаются направленными
отрезками.

Что такое вектор?
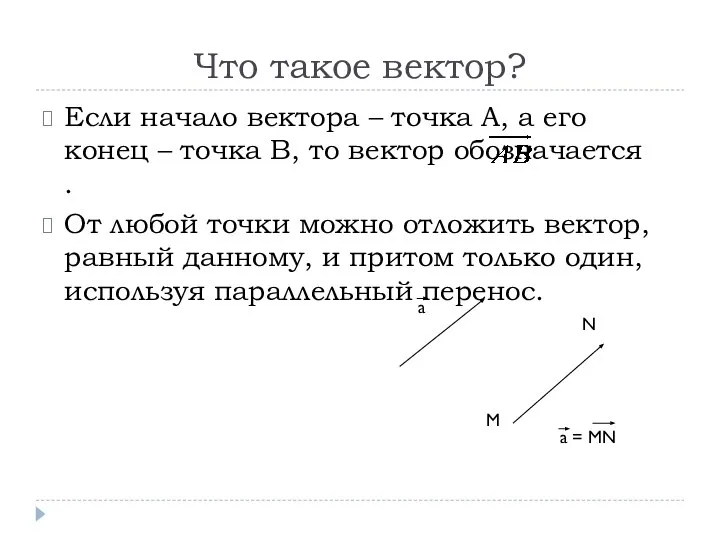
Если начало вектора – точка А, а его конец – точка В, то вектор обозначается .
От любой точки можно отложить вектор, равный данному, и притом только один, используя параллельный перенос.

Виды векторов
Нулевой вектор – точка в пространстве. Начало и конец нулевого вектора совпадают, и он не имеет длины и направления. Обозначается: .
Абсолютной величиной (длиной или модулем) вектора называется длина отрезка, изображающего вектор. Абсолютная величина вектора обозначается .
Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или на параллельных
прямых.

Виды векторов
Если векторы и коллинеарные и их лучи направлены в одну сторону, то векторы называются сонаправленными.
Если векторы и коллинеарные и их лучи направлены в разные стороны, то векторы называются противоположно направленными.
Нулевой вектор считают сонаправленным с любым.

Сложение векторов
Если векторы a и b отложить последовательно друг за другом (начало вектора b попадает в
конец вектора a), то вектор суммы c
соединяет начало одного вектора с концом
второго вектора.
Это правило работает и для коллинеарных
векторов.

Свойства сложения векторов

Сложение нескольких векторов
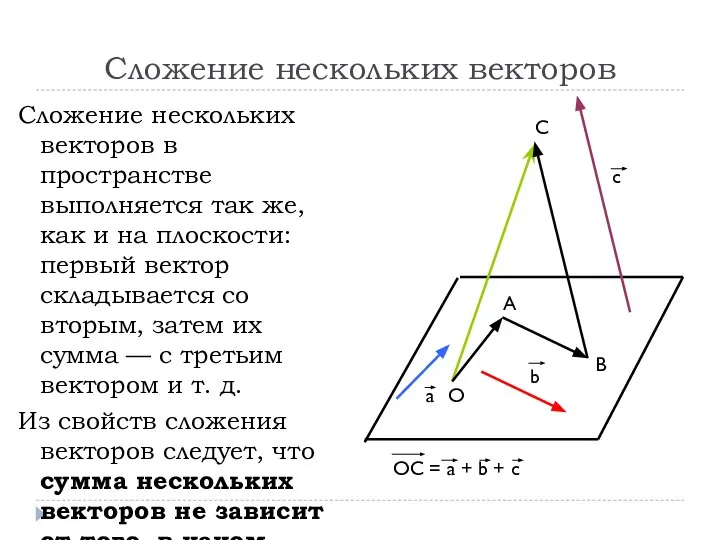
Сложение нескольких векторов в пространстве выполняется так же, как и на плоскости: первый вектор складывается со вторым, затем их сумма — с третьим вектором и т. д.
Из свойств сложения векторов следует, что сумма нескольких векторов не зависит от того, в каком порядке они складываются.

Разность векторов
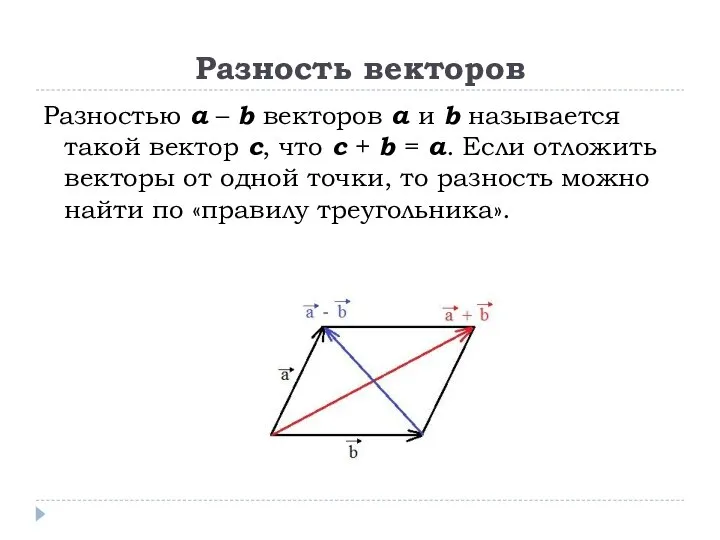
Разностью a – b векторов a и b называется такой вектор c, что c + b = a. Если отложить векторы от одной точки, то разность можно найти по «правилу треугольника».