Вписанные и описанные окружности

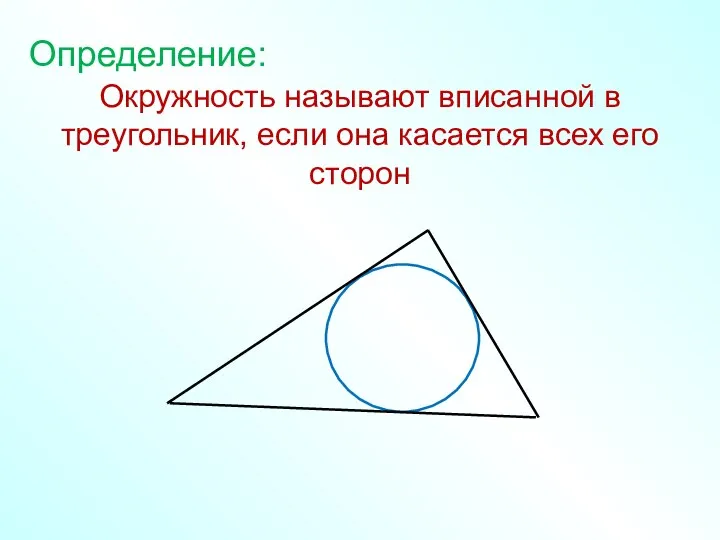
Окружность называют вписанной в треугольник, если она касается всех его сторон
Определение:

Радиус окружности вписанной в прямоугольный треугольник, определяется по формуле
где r – радиус вписанной окружности,
а и b - катеты, c - гипотенуза

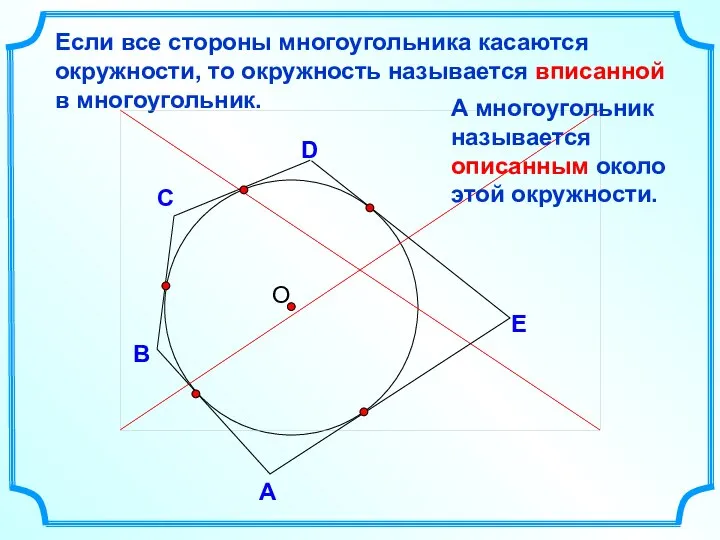
D
В
С
Если все стороны многоугольника касаются окружности, то окружность называется вписанной в многоугольник.
А
E
А многоугольник называется описанным около этой окружности.

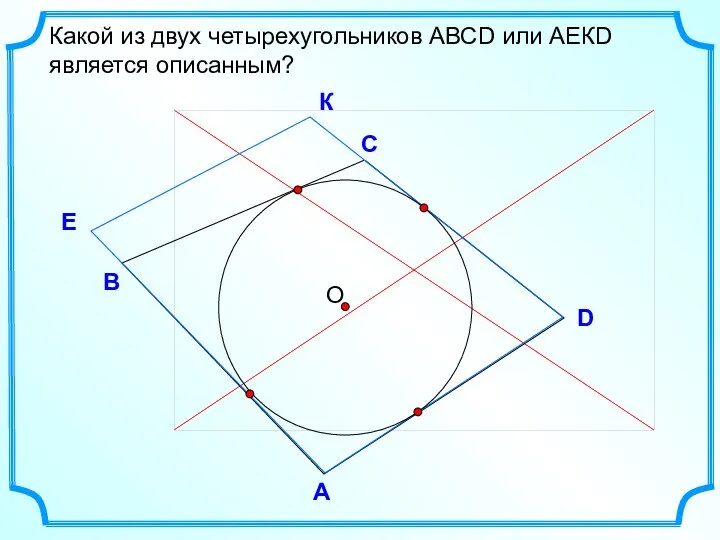
D
В
С
Какой из двух четырехугольников АВСD или АЕКD является описанным?
А
E
К

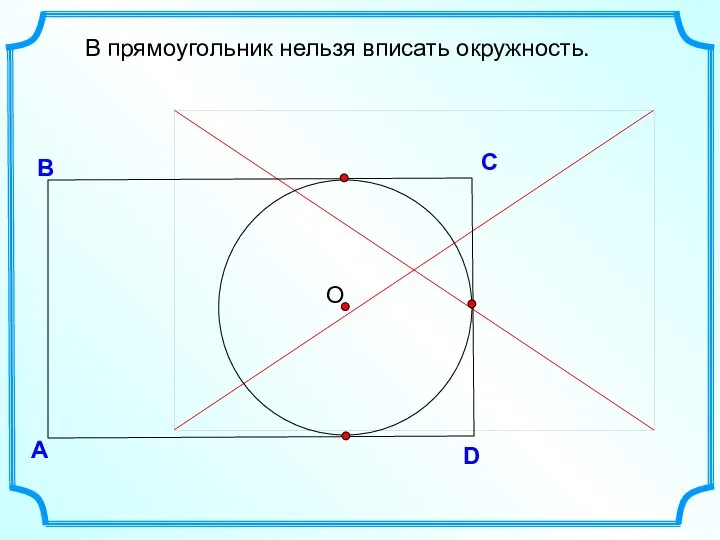
D
В
С
В прямоугольник нельзя вписать окружность.
А

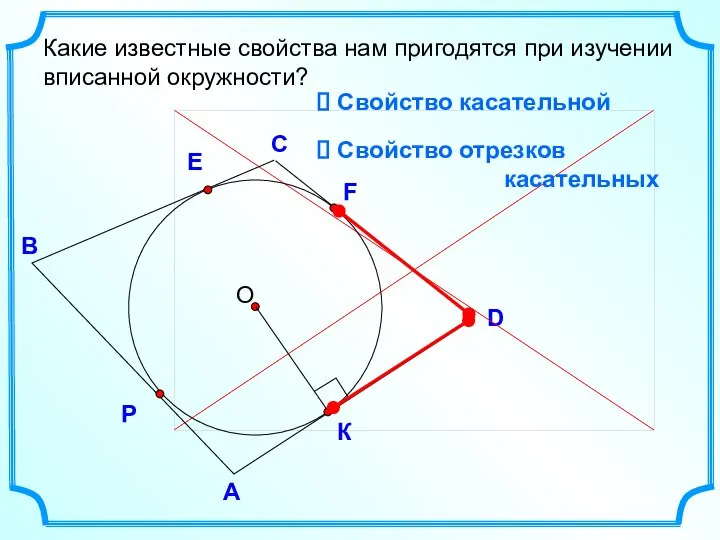
D
В
С
Какие известные свойства нам пригодятся при изучении вписанной окружности?
А
E
Свойство касательной
Свойство отрезков
касательных
F
P

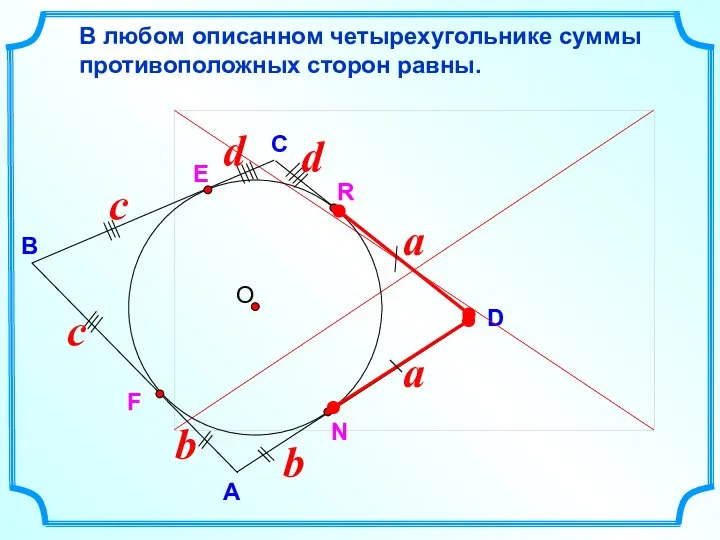
D
В
С
В любом описанном четырехугольнике суммы противоположных сторон равны.
А
E
R
N
F

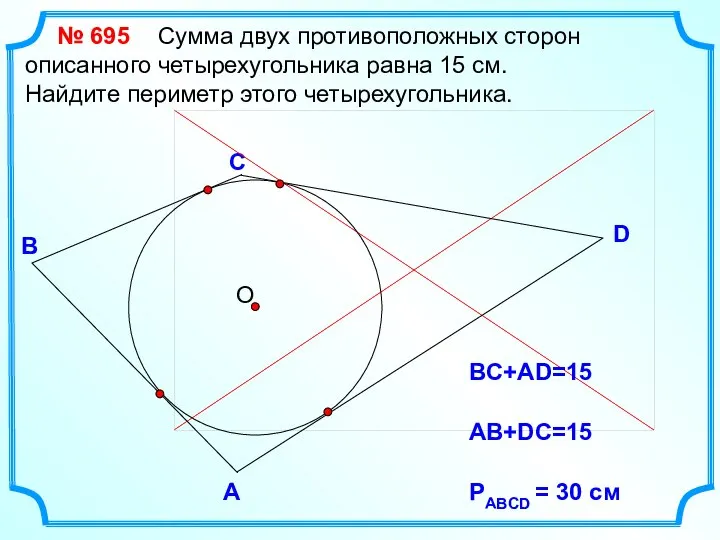
D
В
С
Сумма двух противоположных сторон описанного четырехугольника равна 15 см.
Найдите периметр этого четырехугольника.
А
№ 695
ВC+AD=15
AB+DC=15
PABCD = 30 см

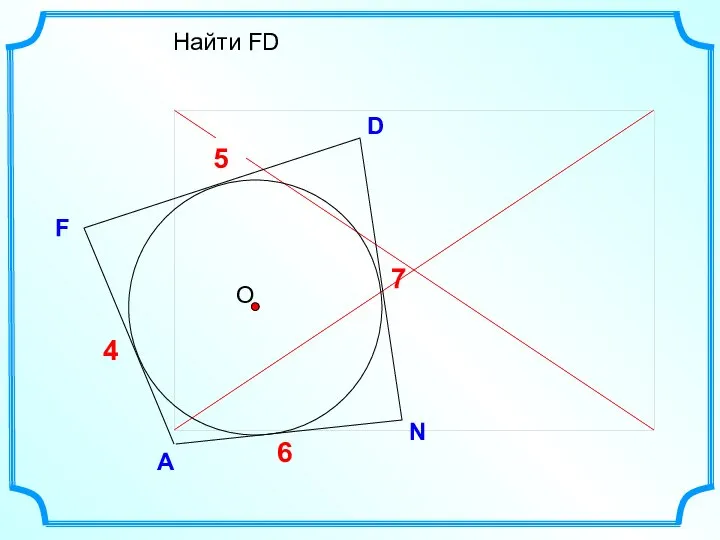
D
F
Найти FD
А
N
?
4
7
6
5

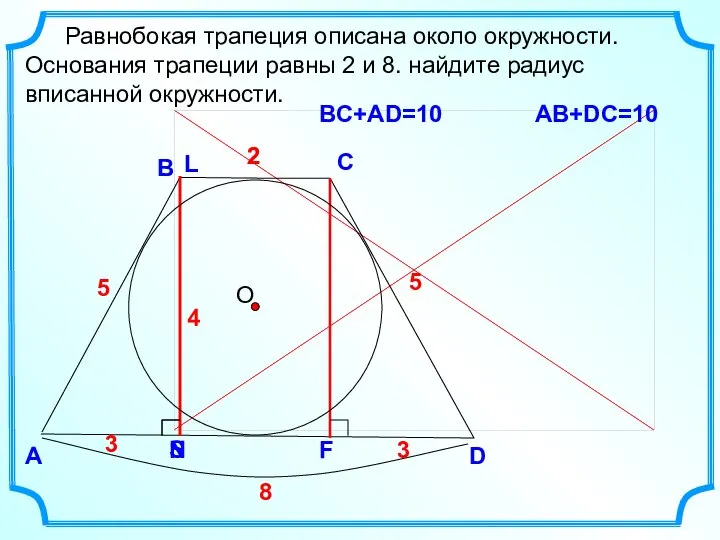
D
В
С
Равнобокая трапеция описана около окружности. Основания трапеции равны 2 и 8. найдите радиус вписанной окружности.
А
ВC+AD=10
AB+DC=10
2
8
2
4

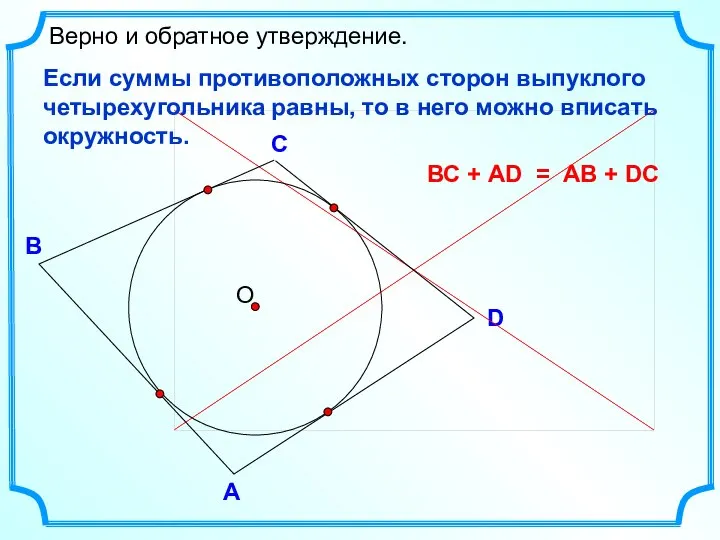
D
В
С
Верно и обратное утверждение.
А
Если суммы противоположных сторон выпуклого четырехугольника равны, то в него можно вписать окружность.
ВС + АD = АВ + DC

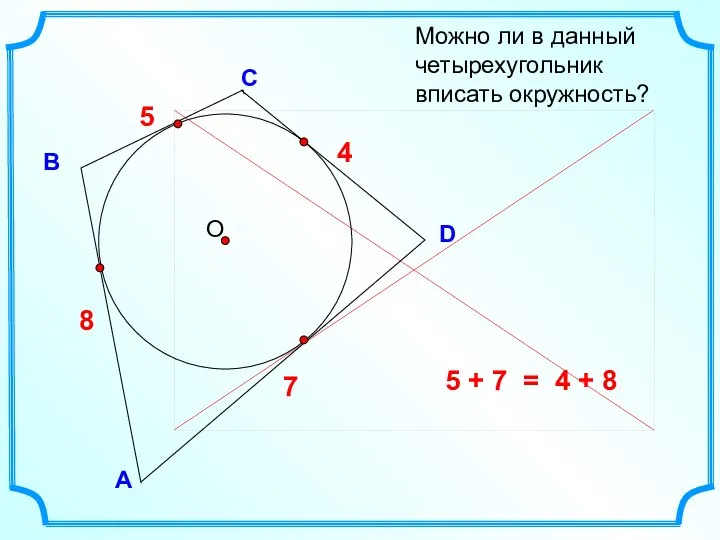
D
В
С
Можно ли в данный четырехугольник вписать окружность?
А
5 + 7 = 4 + 8
5
7
4
8

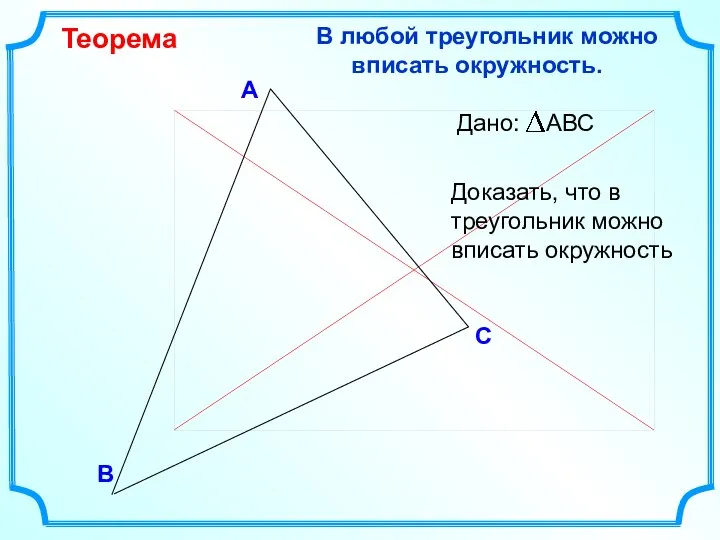
В
С
А
В любой треугольник можно вписать окружность.
Теорема
Доказать, что в треугольник можно вписать окружность

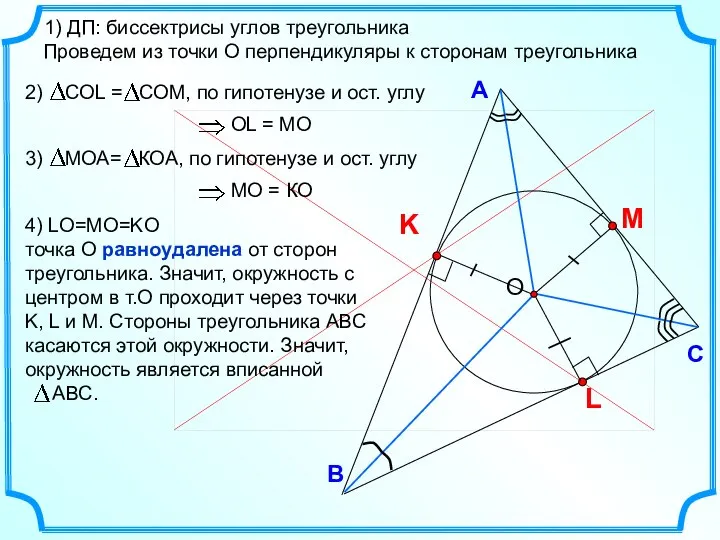
В
С
А
1) ДП: биссектрисы углов треугольника
Проведем из точки О перпендикуляры к сторонам треугольника

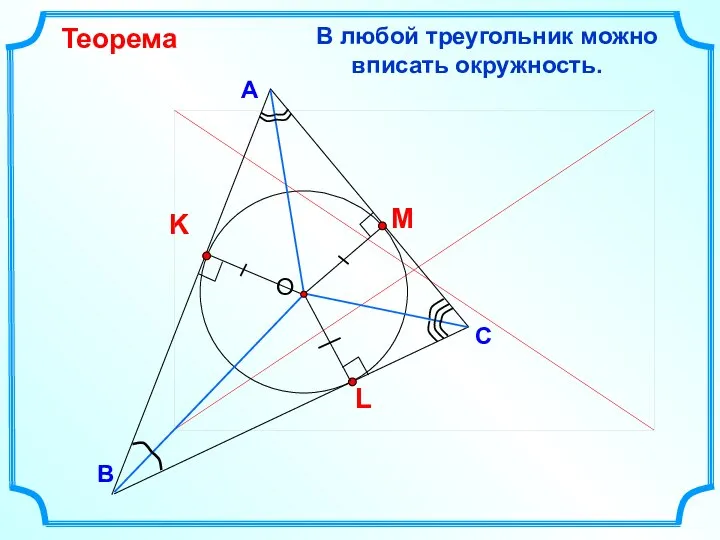
В
С
А
В любой треугольник можно вписать окружность.
Теорема

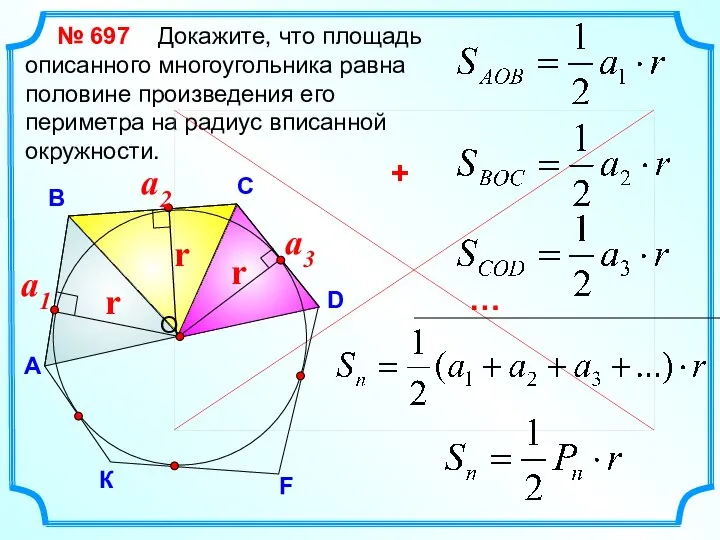
D
В
С
Докажите, что площадь описанного многоугольника равна половине произведения его периметра на радиус вписанной окружности.
А
№ 697
F
a1
a2
a3
…
К

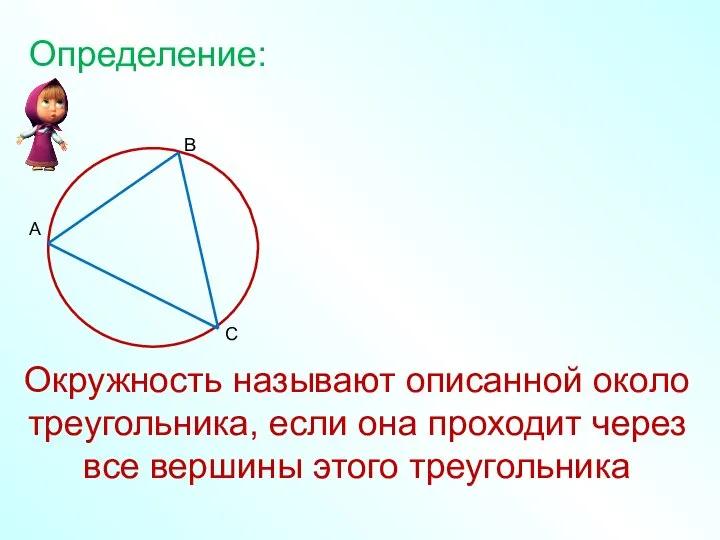
Окружность называют описанной около треугольника, если она проходит через все вершины этого треугольника
Определение:

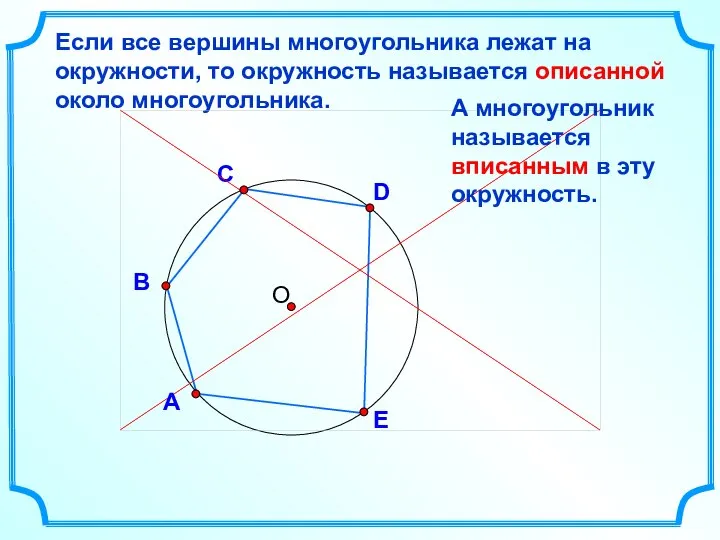
D
В
С
Если все вершины многоугольника лежат на окружности, то окружность называется описанной около многоугольника.
А
E
А многоугольник называется вписанным в эту окружность.

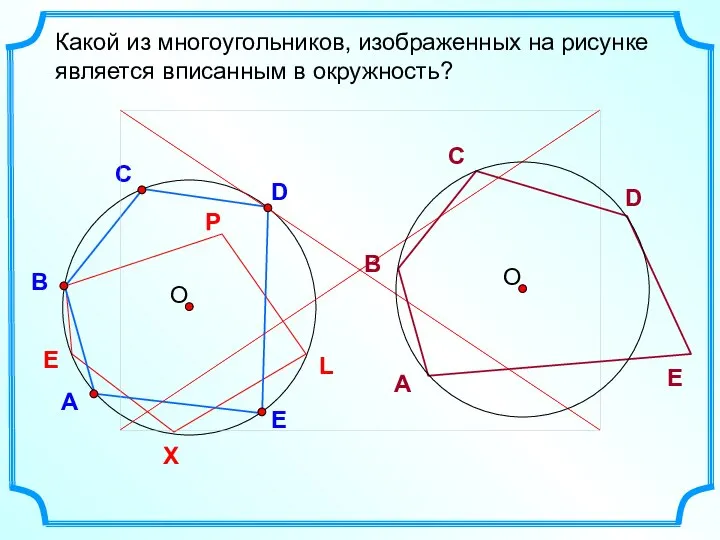
D
В
С
Какой из многоугольников, изображенных на рисунке является вписанным в окружность?
А
E
L
P
X
E

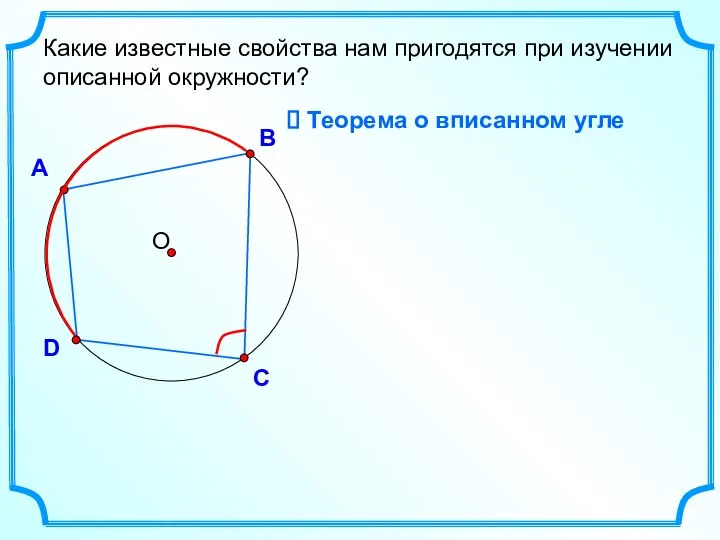
А
В
D
С
Какие известные свойства нам пригодятся при изучении описанной окружности?
Теорема о вписанном угле

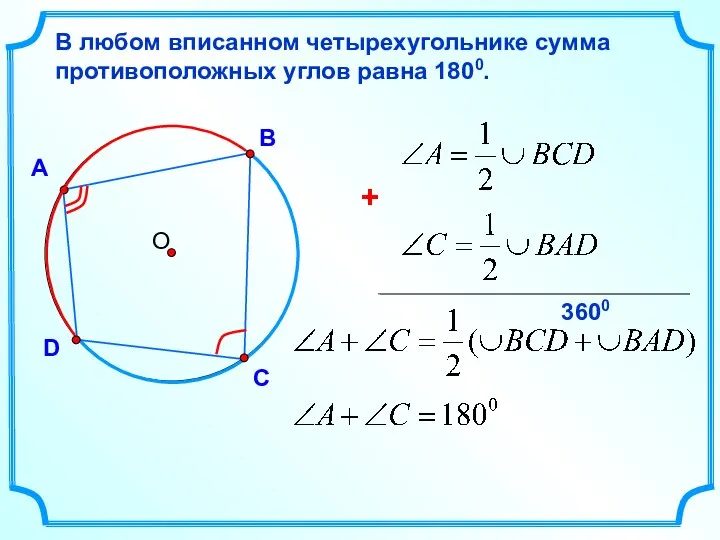
А
В
D
В любом вписанном четырехугольнике сумма противоположных углов равна 1800.
С
3600

?
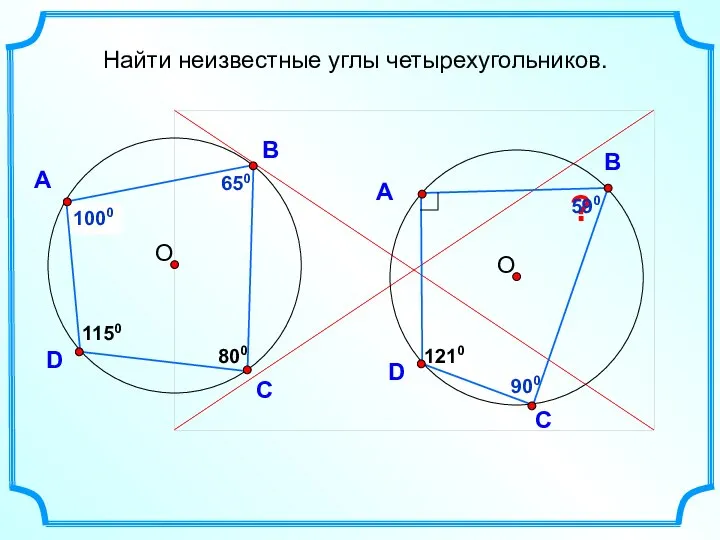
590
?
900
?
650
?
1000
D
А
В
С
800
1150
D
А
В
С
1210
Найти неизвестные углы четырехугольников.

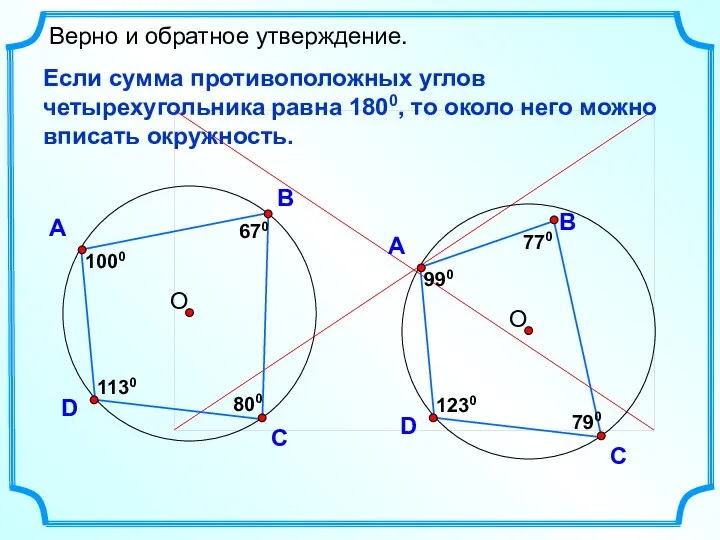
D
Верно и обратное утверждение.
Если сумма противоположных углов четырехугольника равна 1800, то около него можно вписать окружность.
А
В
С
800
1000
1130
670

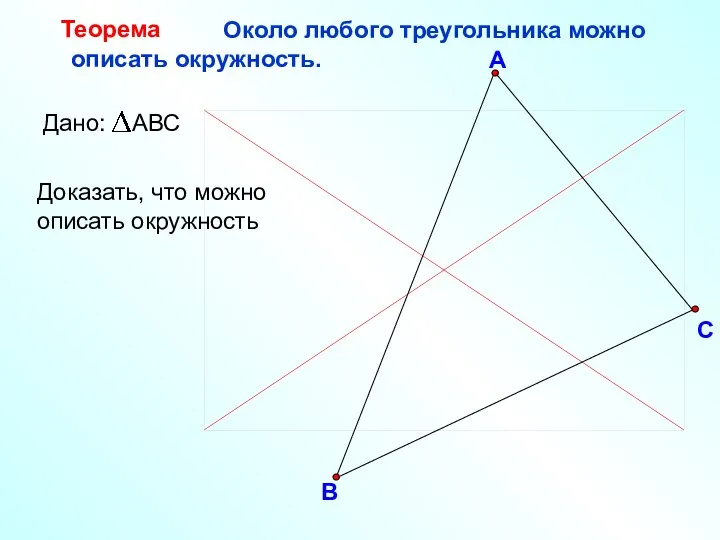
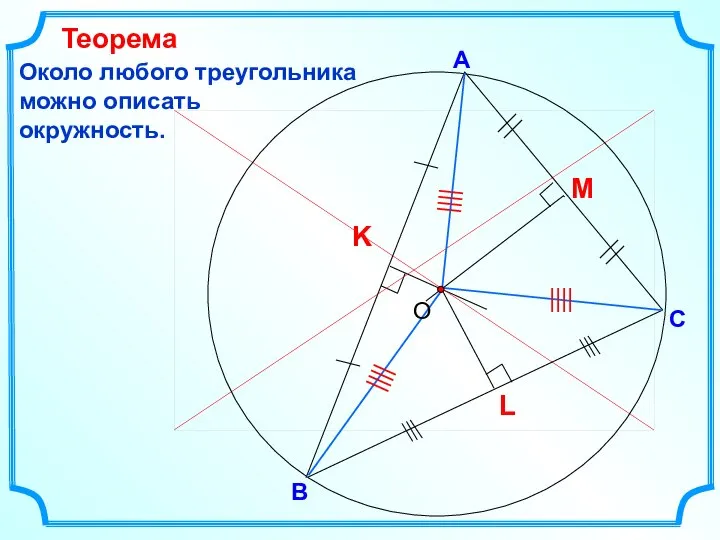
В
С
А
Около любого треугольника можно
описать окружность.
Теорема
Доказать, что можно описать окружность

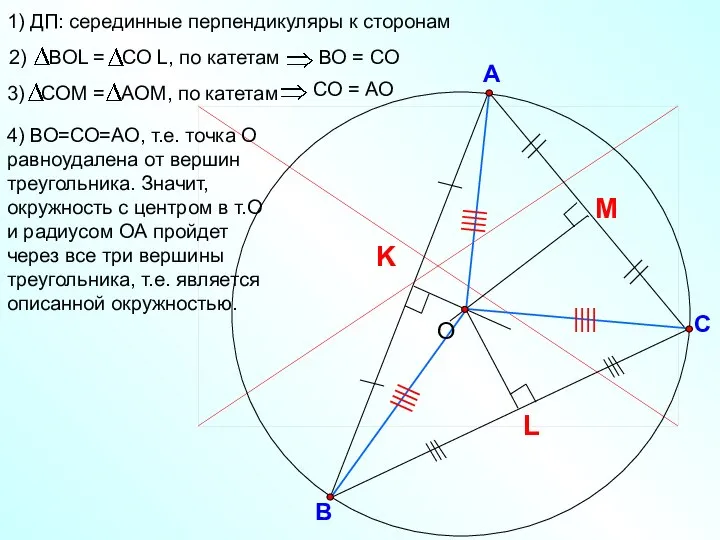
В
С
А
1) ДП: серединные перпендикуляры к сторонам
4) ВО=СО=АО, т.е. точка О равноудалена от вершин треугольника. Значит, окружность с центром в т.О и радиусом ОА пройдет через все три вершины треугольника, т.е. является описанной окружностью.

В
С
А
Около любого треугольника можно описать
окружность.
Теорема

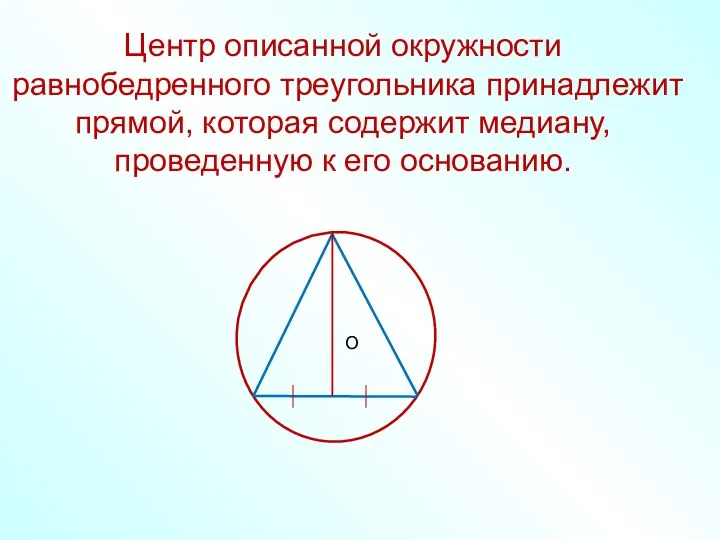
Центр описанной окружности равнобедренного треугольника принадлежит прямой, которая содержит медиану, проведенную к его основанию.
О

Центр вписанной окружности равнобедренного треугольника принадлежит высоте, проведенной к его основанию
О

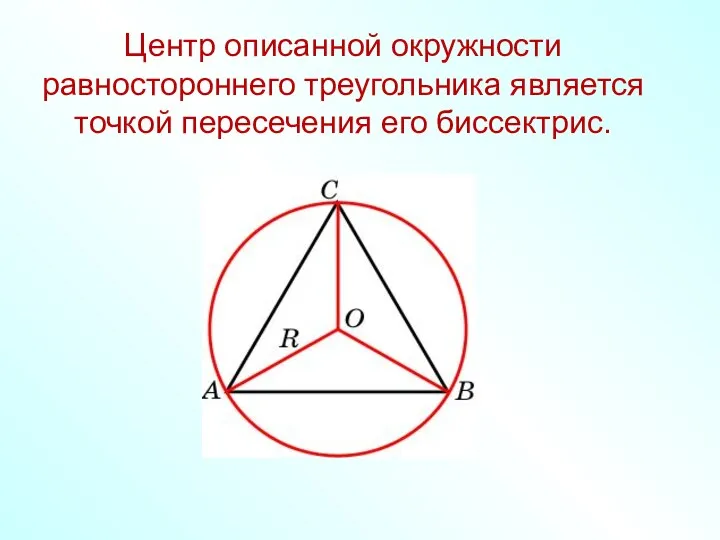
Центр описанной окружности равностороннего треугольника является точкой пересечения его биссектрис.

Если центр окружности, описанной около треугольника принадлежит его стороне, то треугольник - прямоугольный

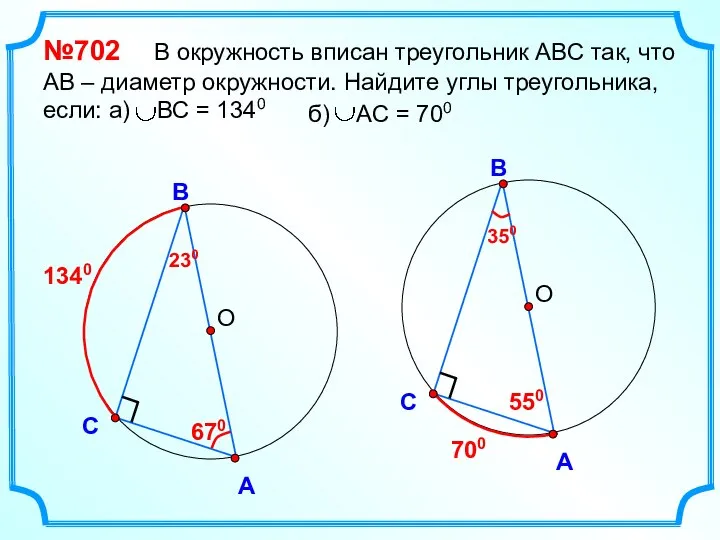
О
В
С
А
№702 В окружность вписан треугольник АВС так, что АВ – диаметр окружности. Найдите углы треугольника, если: а) ВС = 1340
1340
670
230
700
550
350

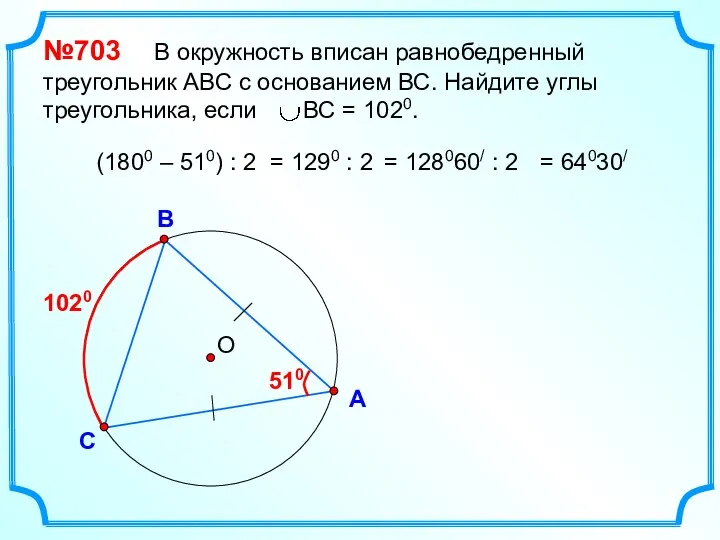
О
В
С
А
№703 В окружность вписан равнобедренный треугольник АВС с основанием ВС. Найдите углы треугольника, если ВС = 1020.
1020
510
(1800 – 510) : 2
= 1290 : 2
= 128060/ : 2
= 64030/

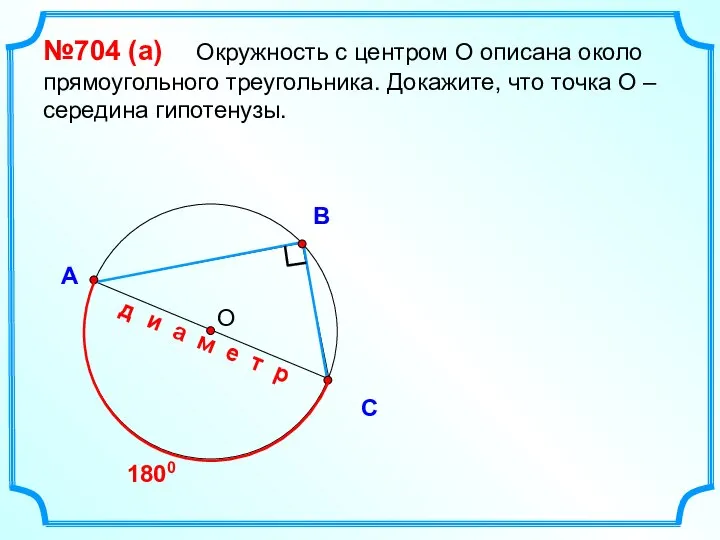
В
С
А
№704 (a) Окружность с центром О описана около прямоугольного треугольника. Докажите, что точка О – середина гипотенузы.
1800
д и а м е т р

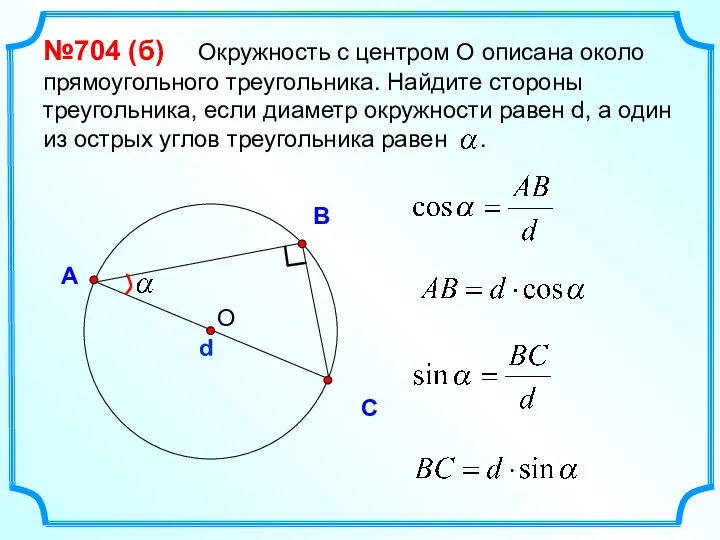
В
С
А
№704 (б) Окружность с центром О описана около прямоугольного треугольника. Найдите стороны треугольника, если диаметр окружности равен d, а один из острых углов треугольника равен .
d

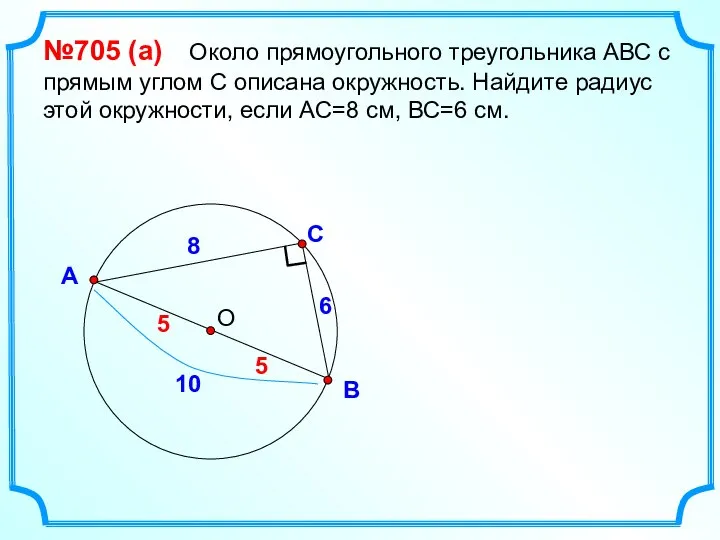
С
В
А
№705 (а) Около прямоугольного треугольника АВС с прямым углом С описана окружность. Найдите радиус этой окружности, если АС=8 см, ВС=6 см.
8
6

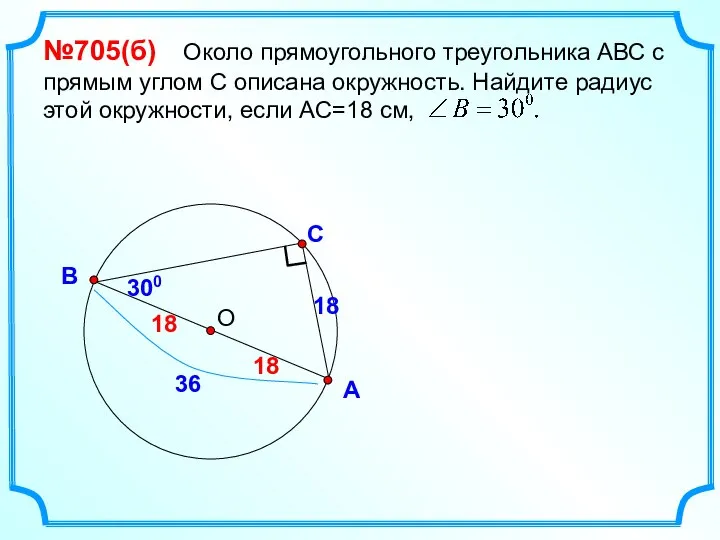
С
А
В
№705(б) Около прямоугольного треугольника АВС с прямым углом С описана окружность. Найдите радиус этой окружности, если АС=18 см,
18
300

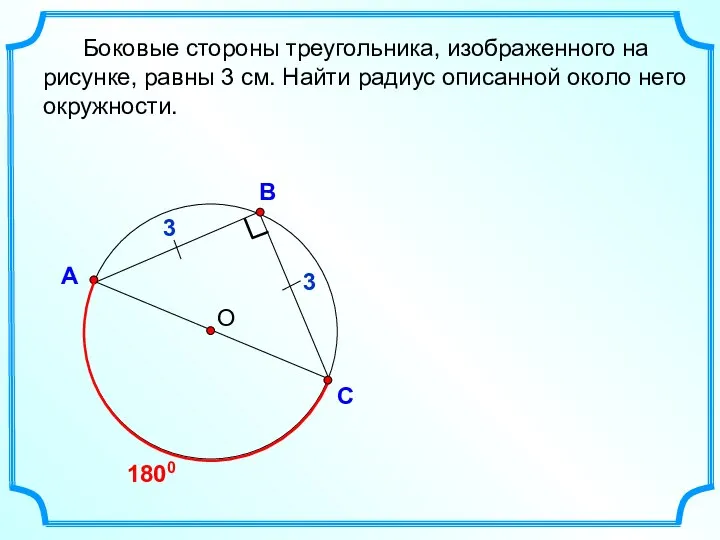
О
В
С
А
Боковые стороны треугольника, изображенного на рисунке, равны 3 см. Найти радиус описанной около него окружности.
1800
3
3