Содержание
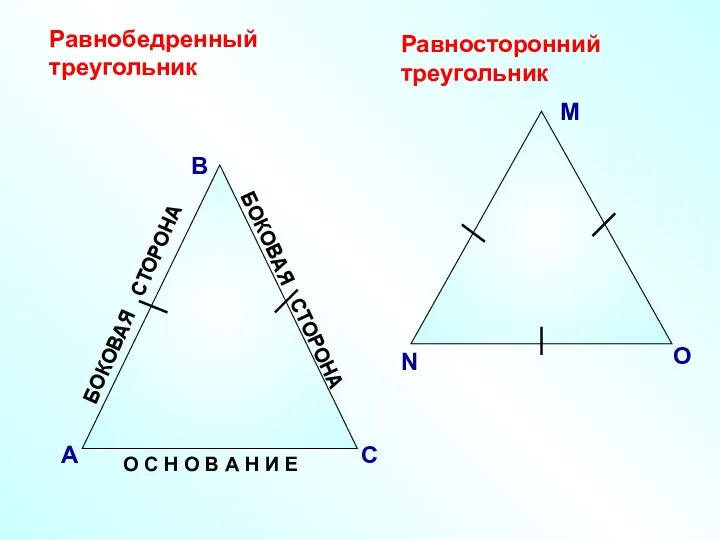
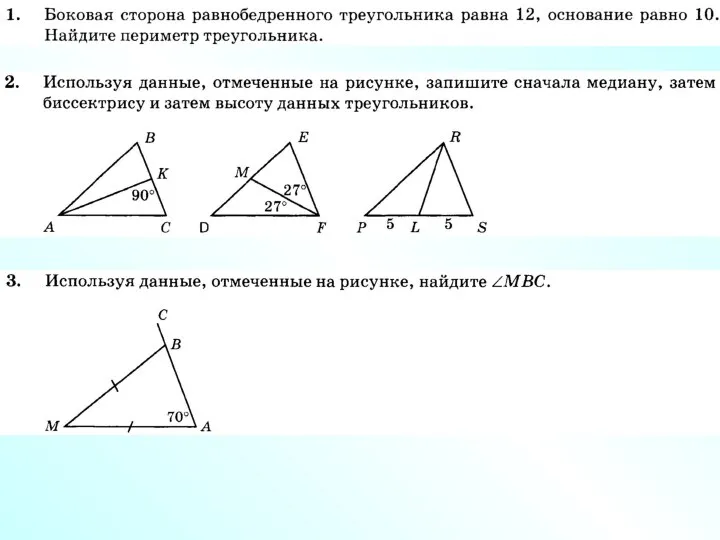
- 2. В А С Равнобедренный треугольник О С Н О В А Н И Е БОКОВАЯ СТОРОНА
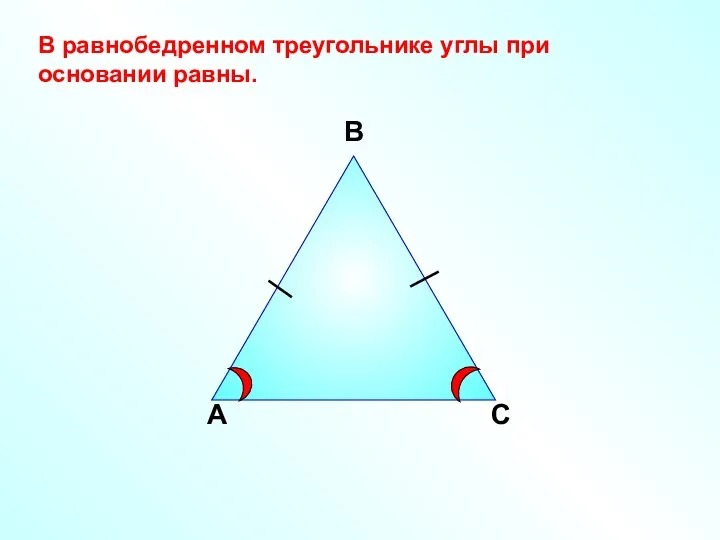
- 3. А В С В равнобедренном треугольнике углы при основании равны.
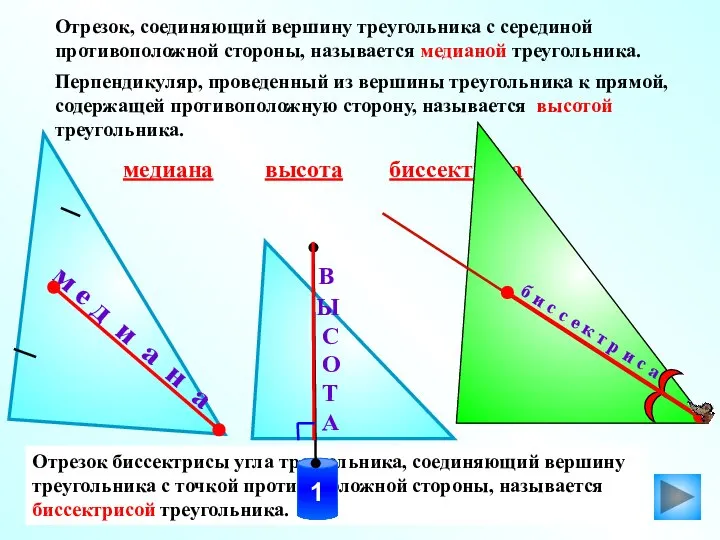
- 4. м е д и а н а Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой
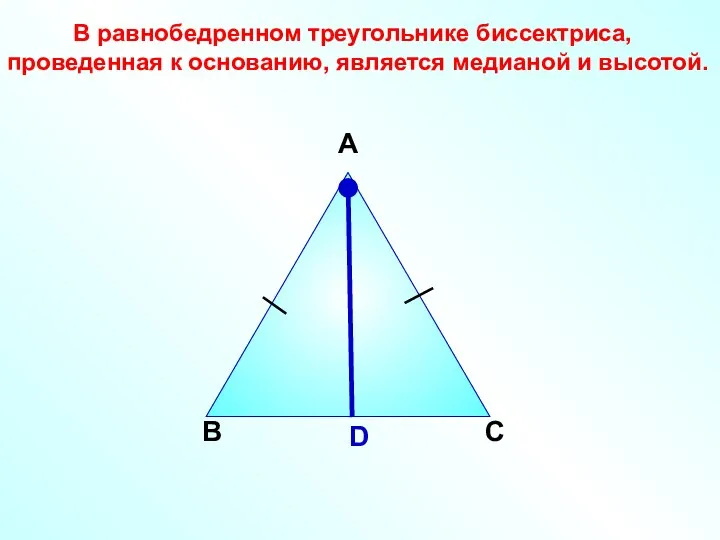
- 5. В А D С В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.
- 9. * К л а с с н а я р а б о т а. Второй
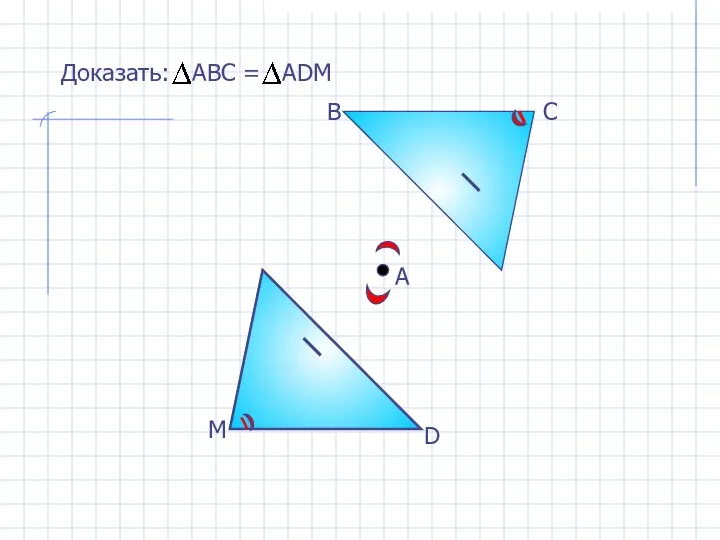
- 10. D М А В С
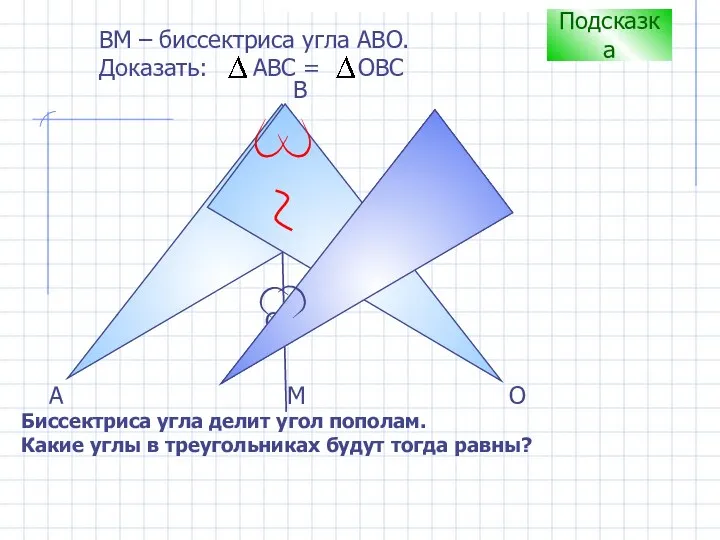
- 11. С B А ВM – биссектриса угла АВО. Доказать: АВС = ОВС Подсказка Биссектриса угла делит
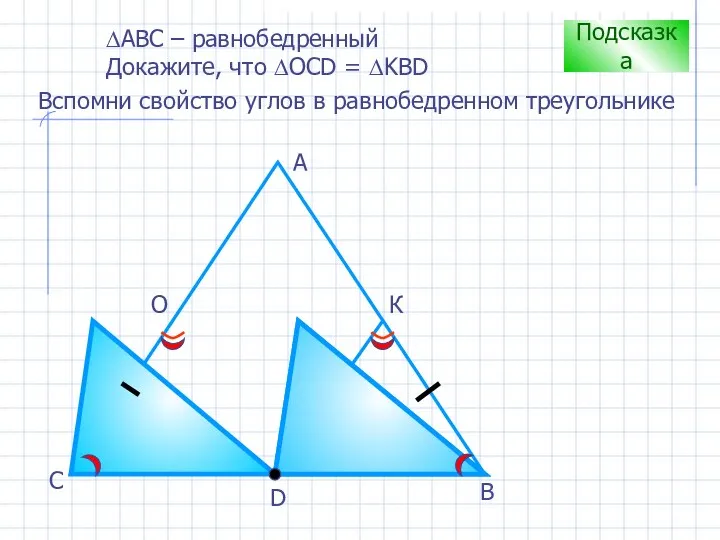
- 12. D В С А О К Подсказка Вспомни свойство углов в равнобедренном треугольнике ∆АВС – равнобедренный
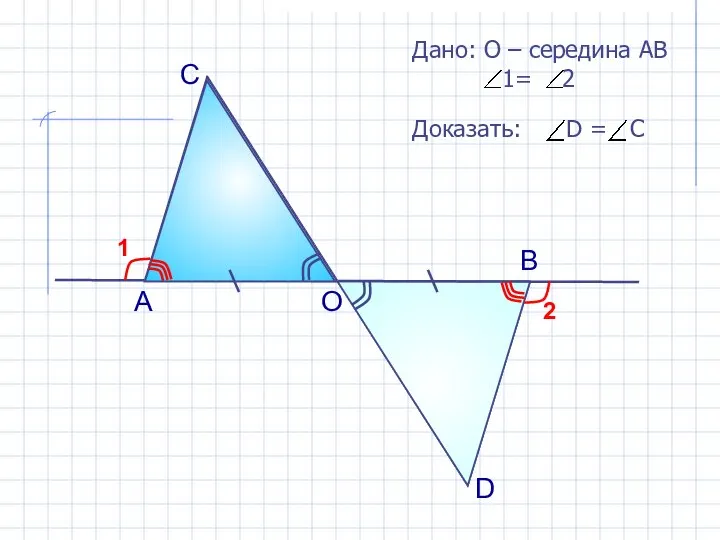
- 13. А О В С D 1 2
- 15. Скачать презентацию


 Ракеты и символы
Ракеты и символы Решение задач. Урок 22
Решение задач. Урок 22 1-2_1
1-2_1 Презентация на тему Полупрямая
Презентация на тему Полупрямая  Признаки подобия треугольников (урок-практикум)
Признаки подобия треугольников (урок-практикум) Проценты. Устный математический диктант
Проценты. Устный математический диктант Треугольники. Часть 1
Треугольники. Часть 1 Площади многогранников
Площади многогранников Задачи практического характера в разных областях науки и техники
Задачи практического характера в разных областях науки и техники Решение заданий с производной
Решение заданий с производной Сложение дробей с разными знаменателями
Сложение дробей с разными знаменателями Слагаемое. Сумма. 1 класс
Слагаемое. Сумма. 1 класс Иррациональные неравенства
Иррациональные неравенства Метод наименьших квадратов. Ordinary Least Squares, OLS
Метод наименьших квадратов. Ordinary Least Squares, OLS Объём параллелепипеда. Задачи
Объём параллелепипеда. Задачи Взаимно обратные числа
Взаимно обратные числа Тренинг по математике
Тренинг по математике Понятие предела функции
Понятие предела функции Цифры от 0 до 9
Цифры от 0 до 9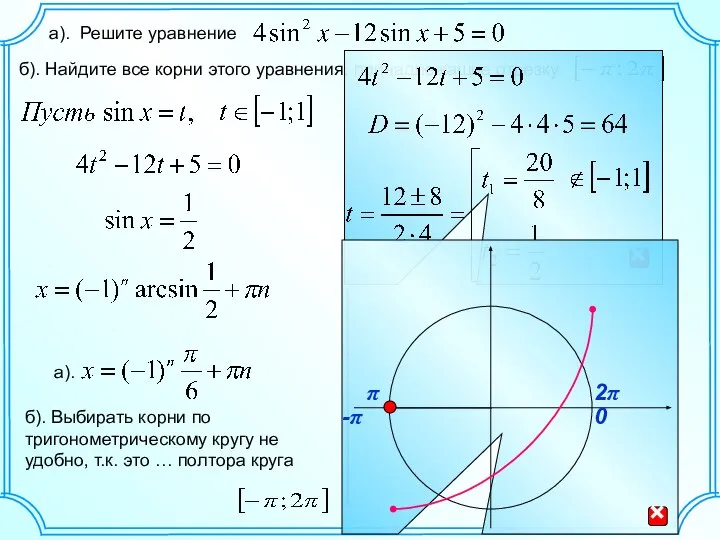 Решение уравнений C 22, по тригонометрии
Решение уравнений C 22, по тригонометрии Прямое сложение и вычитание
Прямое сложение и вычитание Производная сложной функции
Производная сложной функции Деление на двузначное число
Деление на двузначное число Планы второго порядка
Планы второго порядка Свойства бинарных отношений
Свойства бинарных отношений Решение простейших тригонометрических уравнений с помощью единичной окружности
Решение простейших тригонометрических уравнений с помощью единичной окружности Методы решения экстремальных задач
Методы решения экстремальных задач Бинарный урок физики и геометрии
Бинарный урок физики и геометрии